数据基故障诊断算法更新问题研究*

赵晨旭，涂 遗，邱 静，刘冠军

(国防科技大学 装备综合保障技术重点实验室， 湖南 长沙 410073)

1 问题分析

机内测试系统是传感器、数据处理器、诊断软件等部分结合的产物，作为装备的一部分，可以使使用者尽快开展故障诊断与预测。随着计算机技术的不断发展，基于机器学习的故障诊断，尤其是基于数据的分类在故障检测与隔离过程中受到了越来越多的重视和应用[1]。将传感器采集到的数据经过一定的数据处理后得到装备运行的实时特征，将其与装备研制和运行中累积的运行状态“知识”作对比，可快速确定装备的运行状态。对于基于机器学习的故障诊断算法，足够的训练样本是保证得到高精度诊断结论的必要条件，只有经过充分训练的算法才能达到故障诊断设计要求。由于装备实际工作剖面复杂多样，在装备测试性设计时，受限于设计时间和经费，上述前提一般是不成立的；尤其是设计之初，往往难以得到装备故障数据的全样本空间，对于缺少相似产品的新研装备而言，得到正常状态的全样本空间通常也是比较困难的。在这种情况下，为了保证诊断结论的准确性，故障诊断决策算法需要随着试验或者使用过程中数据的累积而不断迭代更新[2]。在这个过程中，机器学习算法通常面临着分类器更新训练问题[3-5]、训练样本不平衡问题[6-8]和硬件存储容量限制[9]等问题。随着机器学习热度的不断增加，上述问题受到了越来越多的关注。但是从目前的文献来看，成果多集中在某个单一问题的解决上，统筹考虑上述三个问题，提出一套系统解决方案的成果还未发现。针对该情况，本文试图提出一套简单实用的方法，解决在测试性设计改进过程中如何开展诊断算法更新工作的问题。

2 问题解决

2.1 基于密度的大样本数据压缩

数据压缩是一种用少量样本表征完整原始样本集大部分特征区域的数据缩减方法[10]。基于密度的聚类是常用的聚类方法之一，本文参考该方法开展大样本数据压缩，在缓解样本量不平衡的同时，解决算法更新时原始样本不断增多、存储耗费大的问题。

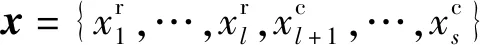
(1)

式(1)右侧第一项为用欧氏距离表征的实数特征距离，第二项为用相异匹配测度表征的属性特征距离，λ用以调整属性特征在距离测度中的权重，δ(·)为示性函数。

(2)

根据定义，d(xi,xj)可以用来衡量两个样本之间的相似程度：d(xi,xj)=0时，两个样本最相似，甚至相同；距离越大，两个样本之间的相似性越差。

对于容量为N的样本集，在距离函数的基础上，可以用式(3)定义任一样本x附近的样本分布密度。

(3)

ρ(x)越大说明样本集中与样本x相似的样本点越多；反之则说明样本集中与样本x相似的样本点较少。

定义以xi为中心、以ε为半径的超球为xi的ε邻域，令Nε(xi,X)表示样本集X与该邻域交集的样本点个数，则Nε(xi,X)越大，表示ρ(xi)越大。 对于阈值q，若Nε(xi,X)≥q，则可称xi为样本集的核心对象。 核心对象通常作为代表样本点被保留至代表样本集中。 根据定义可知，ε越大，核心对象需要代表的区域越大，核心对象数量越少;q越大，核心对象的代表性越强，核心对象数量也越少。 于是通过调整{ε,q}取值可调整代表样本集的样本个数。 为保证代表样本点的均匀分布，在实际应用中通常令q=1，通过调整ε取值控制代表样本容量，样本数量随着ε的减小而增多。

令Xun表示待选样本集，其中待选样本按ρ(x)取值从大到小的顺序依次编号。 令P={p1,…,pND}表示数据压缩后得到的代表样本集，其中ND为要求的代表样本集容量，于是可以给出如算法1所示的代表样本集生成过程。 该代表样本集即可作为数据压缩后的训练样本。 该方法能够保证生成的训练样本既涵盖待选样本集的核心对象，又包含奇异特征点，从而张满原始样本集分布空间。

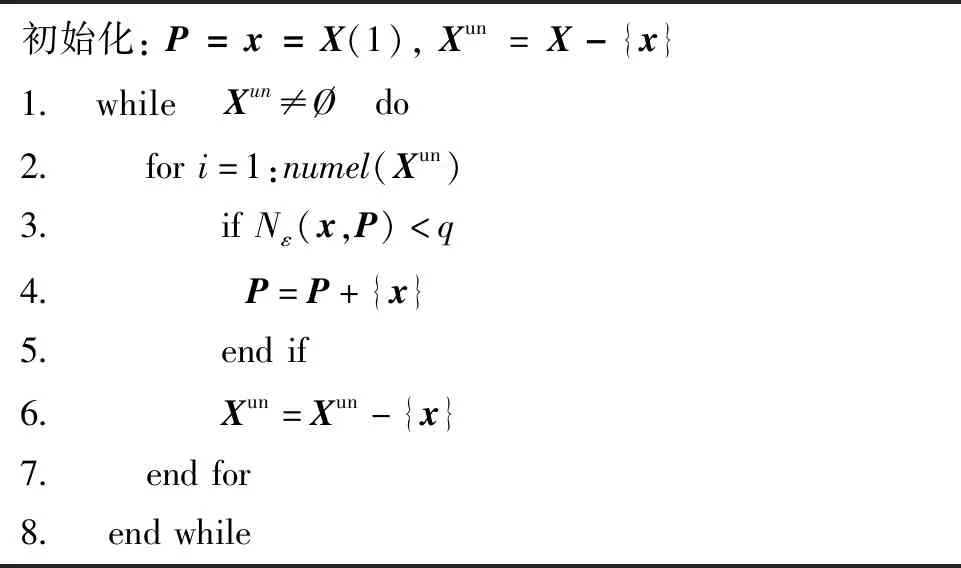
算法1 获取代表样本集Alg.1 Get the sample set

2.2 基于人工免疫的小样本数据扩充

基于启发式算法的数据扩充是常见的伪数据生成方法之一。特征联合分布密度函数是启发式样本扩充的基础。随着特征维数的增高，联合分布函数也会逐渐复杂，并且当数据量较小时通常难以得到准确的分布函数参数估计。受人工免疫系统[12]启发，将原始样本x看作抗原，与免疫系统生成的抗体组成新样本集，则可以在扩充样本容量的同时，丰富数据分布的多样性，并且该方法不需要给出特征联合分布函数，具体流程如下。

Step1：计算原始样本集X中每个样本x的分布密度系数ρ(x)，同时随机生成样本集X对应的未成熟抗体种群A。

Step2：对原始样本集X中的每个样本x执行如下步骤：

1)计算未成熟抗体种群A中每个抗体aj与原始样本x的亲和度Afj=1/d(aj,x)，其中d(aj,x)如式(1)所示。

由于属性特征的取值通常是有限并且少量的，如果对其进行变异操作，极可能产生大量实际上不存在的样本属性特征，从而引入不必要的人为分类误差。于是，本文对属性特征采取不变异仅繁殖的处理方法。

利用上述过程进行样本扩充，既能保持原样本的重要信息，又能得到多种近似样本。通过控制参数{n,T}取值可以调整扩充样本集的容量，调整参数α∈[0,1]取值能够控制新样本与原始样本的相似程度，α取值越大，新样本与原始样本相似度越高。

2.3 基于代表样本点的混合学习

常见的分类器更新学习方法主要包括批量学习和增量学习两种。传统的批量学习虽然能够较好地处理样本容量限制与知识空间退化的矛盾，但算法更新需要利用所有历史样本，导致存储开销大，并且随着训练样本的增多，更新训练时间也相应变长。传统的增量学习虽然能解决历史样本存储的问题，但是又可能存在知识空间随学习过程逐渐退化的问题。本文提出基于代表样本点的混合学习方法，力图在缓解训练样本存储和算法更新训练时间成本的同时，又能较好地解决知识空间退化的问题。第i+1次支持样本集与诊断算法更新过程如下。

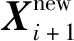
Step2：将P′i+1和原有代表样本集Pi合并后，按照式(4)对合并后的样本集进行元素合并，得到新的临时代表点。

Step3：不断重复Step2直至元素个数满足要求，即可获得用于第i+1次算法更新的最终代表样本集Pi+1。

(4)

3 案例应用

Coraddu等利用Combined Diesel Electric And Gas公司建立的护卫舰推进系统仿真模型开展了大量的数值仿真，并获得了丰富的推进系统运行仿真数据[13-14]。本文利用Coraddu等在加利福尼亚大学尔湾分校机器学习数据库中提供的数据验证第2节所研究方法的有效性。根据文献[14]，燃气机压缩系统退化量kMc和燃气机总体退化量kMt能够较好地表征推进系统故障状态，但这两个参数需要利用16种信号综合建模获取。

按照kMc和kMt的取值，当满足kMc∈[0.95,0.97)∪kMt∈[0.975,0.985)时认为系统处于故障状态，机内测试设备(Built-In Test Equipment, BITE)需要及时报警；否则认为系统处于正常状态，BITE无须报警。

3.1 数据准备

相关研究表明，当用于分类的特征属性过多时可能降低分类效果，因此本文选用了如表1所示的7种测试信号开展系统故障诊断。需要说明的是，选用这些信号并不能说明这些信号是最佳信号，仅能说明这些信号能够较好地验证本文所述方法的有效性。另外为了绘图展示的方便，后文仅选用左侧螺旋桨推进扭矩和涡轮机出口温度两个参数来绘制二维图形。

表1 推进器监测信号Tab.1 Monitored signals of the propulsion plant

为了模拟设计改进过程中因受限于时间和经费，仅能获取系统部分运行状态数据的情况，本文利用均匀抽样提取了如表2所示的两批训练和测试数据。第一批数据用于模拟原有数据，第二批数据用于模拟新增加数据。

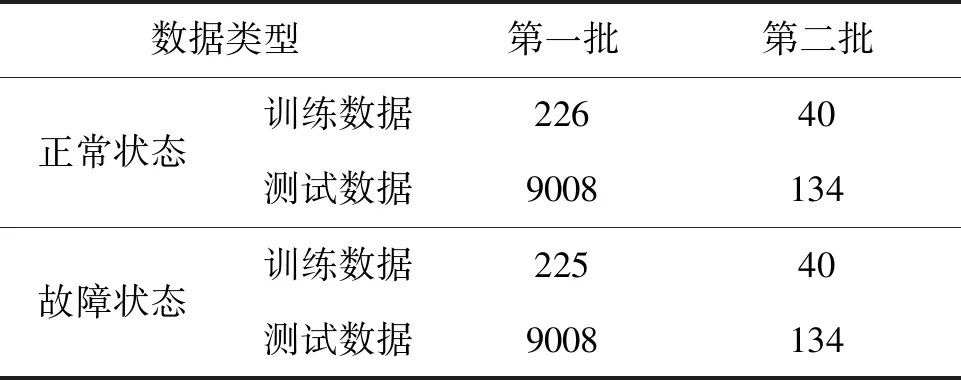
表2 训练与测试用样本集样本数量Tab.2 Data size of the training and testing data

3.2 评价标准

对于BITE设计，故障检测率(Fault Detection Rate，FDR)以及虚警率(Fault Alarm Rate，FAR)是常用评价指标[7]。在概念上，故障检测率与查全率概念相似，用于衡量故障成功检测的概率；虚警率可视为查准率的余集，表征了正常状态被识别为故障状态的概率。

为了与衡量不平衡数据分类效果的F测度相对应，定义如式(5)所示的损失函数，用于对故障检测率和虚警率开展综合衡量。

FL=γFAR+η(1-FDR)

(5)

式中，γ与η分别表示虚警和漏检造成的损失。因为损失函数仅用来定量刻画实际损失，γ与η不必具有实际意义，本文假设虚警和漏检造成的损失相当，并且γ=η=2。

为了评价结果的客观性，采用经典支持向量机(Support Vector Machine, SVM)方法开展故障诊断，未专门研究SVM改进算法改进，而是直接利用MATLAB 2010a软件提供的svmtrain( )函数和svmclassify( )函数开展状态分类，将函数设置高斯核函数，方差0.2，并选用序贯最小优化(Sequential Minimal Optimization, SMO)优化函数作为超平面分类函数。

3.3 性能评估

为了全面验证所提方法有效性，设计两个验证案例：案例A用来验证所提方法在处理数据不平衡方面的应用效果；案例B用来验证基于样本点的混合学习方法在分类器算法更新方面的应用效果。

3.3.1 案例A

Case1：首先利用2.2节所提方法扩大故障状态样本量，使故障状态样本量与正常状态样本量相同。然后利用2.1节所提方法对扩充后的故障样本和原始正常样本进行数据压缩，并设定代表样本集的容量限制为90～100。最后将处理后的代表样本集作为训练样本。

Case2：首先利用2.1节所提方法对原始正常状态样本进行数据压缩，然后和原始故障状态样本组成训练样本集。

Case3：首先利用2.2节所提数据扩充方法扩大故障状态训练样本量，使故障状态样本量与正常状态样本量相当，然后和原始正常状态样本组成训练样本集。

Case4：不对原始训练样本进行任何处理，直接将其作为训练样本集。

利用上述4个不同训练样本集训练得到SVM分类器之后，利用3.1节处理的第一批测试数据测试SVM分类效果。为了消除数据处理随机性对分类测试效果的影响，利用一次数据处理结果重复开展了20次SVM训练，并分别开展分类测试，分类效果评价标准的算术平均值如表3所示。

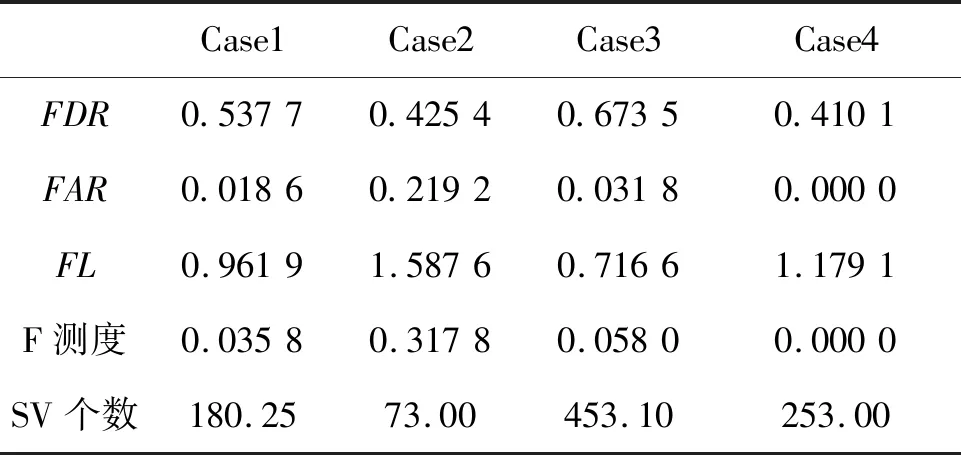
表3 案例A诊断分类平均结果Tab.3 Diagnosis results of scenario A

对比表中数据可知：①前3个示例训练样本集中正常状态与故障状态的样本数量比分别为91 ∶90, 45 ∶40, 200 ∶226，从训练样本数量上看，三种方法都能较好地解决数据不平衡问题；②Case2的故障检测率虽然与Case4接近，但虚警率明显偏高，主要是由于Case2用于训练的数据较少造成分类器识别效果不佳；③Case3的故障检测率比Case4高出50%，同时虚警率也相对较低，主要是因为训练样本量较多，如果不考虑支持向量(Support Vector，SV)个数，可以认为Case3中的数据处理方法最佳；④Case1中故障检测率比Case4提高了将近25%，虚警率也不高，并且与Case3相比，SV个数明显较少；⑤综合SV个数以及分类效果两个评价指标，Case1中的双向数据处理方法既提高了SVM分类准确度，SV的个数也得到了缩减，可以降低诊断算法对机内测试系统存储容量的要求，缩短故障诊断时间。

另外，对比4个示例的F测度和损失函数值可知：损失函数不会因为某个单一因素的极端取值而得到极端结果(如Case4中FAR对F测度的影响)，因此从故障诊断的角度出发，损失函数能比F测度更好地综合反映故障漏检和错检对装备维修造成的损失。

综上所述，由于评价标准不同，在处理具体问题时，是采用单侧数据扩充或压缩，还是采用双侧处理，需要根据实际情况具体判断，但是无论采用何种处理方式，本文所提方法均能较好地解决数据不平衡问题。

3.3.2 案例B

Case1：利用案例A中Case4的支持向量和表2所列的第二批原始训练数据更新SVM，该示例用于模拟简单增量学习过程。

Case2：利用2.3节所提混合学习方法更新SVM，并将正常和故障状态的代表样本集容量分别设置为90～100。

Case3：将表2所列的两批原始训练样本合并组成完整训练样本集，利用传统的批量学习方法更新SVM。

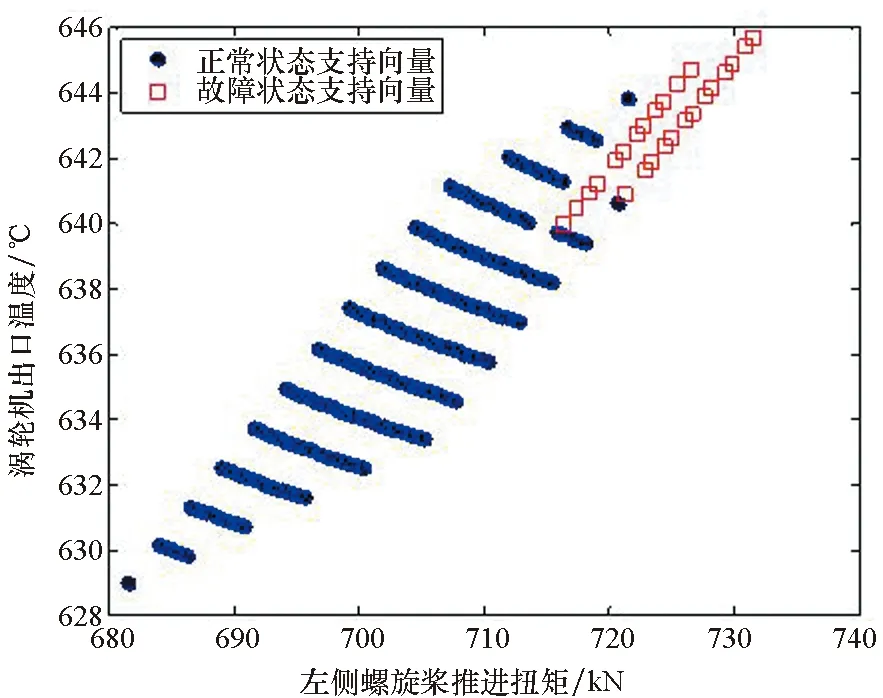
案例B中Case2和Case3用到的训练样本集分别如图1中原始样本和代表样本所示。从图中可以看出原始数据的分布特征在代表样本集中得到了较好的保留。

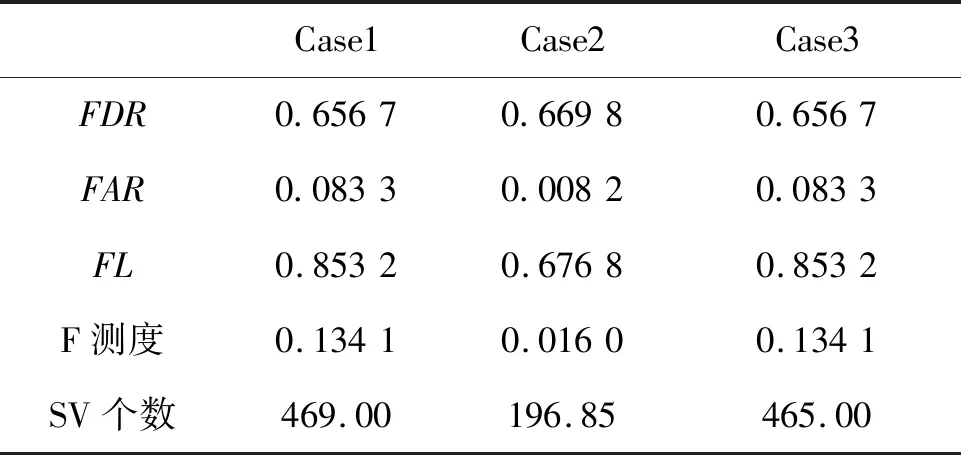
在更新SVM之后，利用表2所列的第二批测试数据验证SVM更新效果。同样，为了降低数据处理随机过程对测试效果的影响，案例B也利用一次数据处理结果进行了20次训练和测试，分类效果的算术平均值如表4所示。图2直观展示了Case1的原支持向量的分布情况。

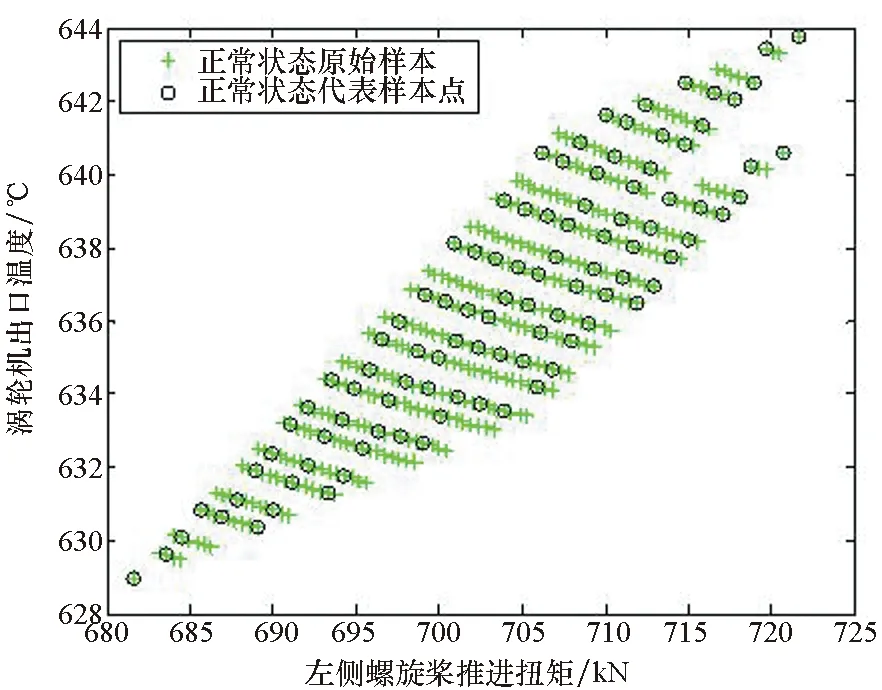
(a) 正常状态下原始样本与代表样本点特征分布(a) Distribution of raw data and delegates in normal state

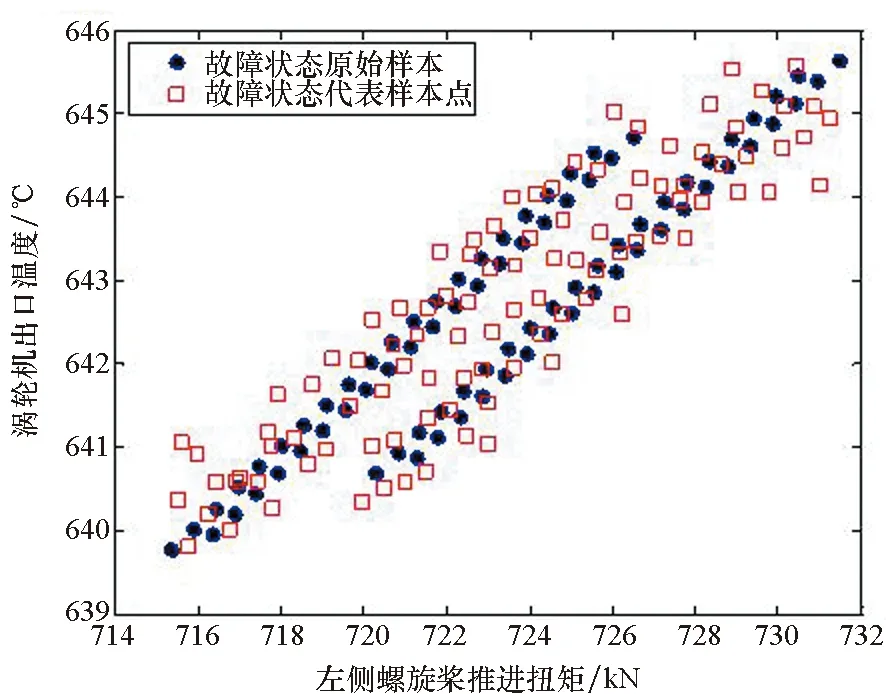
(b) 故障状态下原始样本与代表样本点特征分布(b) Distribution of raw data and delegates in fault state图1 原始数据与代表样本集分布情况Fig.1 Distribution of raw data and delegates set

表4案例B诊断分类平均效果
Tab.4 Diagnosis results of scenario B

Case1Case2Case3FDR0.65670.66980.6567FAR0.08330.00820.0833FL0.85320.67680.8532F测度0.13410.01600.1341SV个数469.00196.85465.00

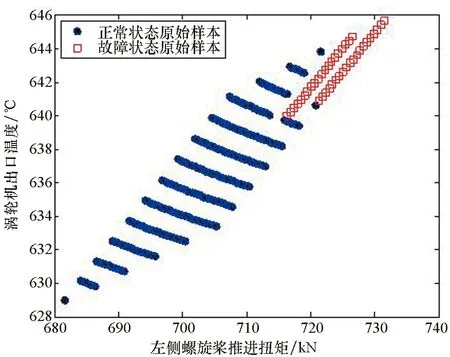
(a) 原始样本特征分布(a) Distribution of raw data

(b) 支持向量特征分布(b) Distribution of SVs图2 Case1原支持向量与第一批原始样本分布Fig.2 Distribution of the original SVs and the 1st batch raw data in Case1

比较表4和图2数据可知：①除了少量故障状态数据外，绝大部分原始训练样本都被处理为Case1的原始支持向量，因此可以认为Case1和Case3的训练样本几乎相同，从而造成Case1和Case3的分类测试结果完全相同；②由于训练样本数量和分布空间的扩充，无论采用哪种方法，故障诊断系统的分类效果与案例A相比都得到了明显提高；③无论是与Case1还是Case3相比，Case2在保持与Case1和Case3几乎相同的故障检测率的同时，虚警率有了明显的下降，并且需要的支持向量数量也明显减少。

4 结论

首先针对数据不平衡问题提出数据压缩方法和数据扩充方法，其中基于密度的大样本数据压缩既能生成满足样本量要求的代表样本集，又能保持较好的原始数据分布规律；基于人工免疫的小样本数据扩充方法在丰富样本数量及分布特征的同时，又有效降低了噪声数据的引入。然后针对分类器更新训练需求给出了一种新的增量式批量学习方法——基于样本代表点的混合学习方法，既可以降低训练样本硬件存储要求，又能缩短分类器更新训练时间，同时保持较高的分类准确性。最后利用公开仿真数据验证了所提方法的有效性。理论分析和仿真结果表明：所提方法可以有效支持基于数据的故障诊断算法更新，并且对其他领域的机器学习应用问题研究也有一定的借鉴意义。