基于位置预测的靶场图像实时判读方法*

钟立军，于起峰，周颉鑫，郭鹏宇，黄 维

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073；2. 军事科学院 国防科技创新研究院， 北京 100071； 3.中国人民解放军95975部队， 甘肃 酒泉 732750)

目前靶场测量方式主要以光学测量为主，基本实现数字图像实时采集和存储，且已具备实时输出图像和视频的能力[1]。但对光测图像的利用主要为景象监视和事后判读处理，未能充分利用图像丰富的信息。而实现图像判读及交会处理的实时化，满足实时控制的需求，对充分利用光测图像非接触、目标信息丰富的特点，提高光学测量在靶场测控的地位有重要在意义，必将成为靶场光测发展的关键方向之一。与事后处理相比，实时处理具有以下优点[2]：①指控人员可根据实测结果实时调整试验方案，使试验任务更加灵活；②实时获取的数据为安控系统提供预警信息，便于突发情况的及时处理；③大幅提高工作效率，使试验与分析同步进行，无须事后集中处理数据。

因为需要进行交会解算或单目多点解算，靶场判读与通常所说的目标跟踪不同，不要求准确给出目标框的位置以及适用目标的大小、姿态变化，而需要准确给出目标同名点位置。其一般过程是由用户手动选择判读点，然后由算法以该点作为跟踪目标，在后续帧上精确定位该点，一般为飞机头部、导弹尾部或者其他同名点等。其难点问题主要有以下几个方面：一是目标情况复杂多变，比如对于导弹而言，存在有火焰和无火焰两种情况，且形状变化大；二是由目标位姿及观测视角变化引起的目标可见部分不一致；三是跟踪过程中目标高速运动会导致图像模糊；四是经纬仪跟踪时会出现随机抖动，导致目标在图像上产生无规律的较大位移甚至跳出视场范围。因此，目前在靶场很难实现自动跟踪，需要大量的人工干预，一般以0.1 s的间隔来进行判读及数据处理，使光测信息不能得到有效利用。

当前比较流行的跟踪方法有Struck、跟踪学习检测算法(Tracking-Learning-Detection, TLD)、 DSST、C-COT、ECO、CREST[3-8]等，都以准确地给出目标的区域作为评价准则，同时尽可能适用目标的缩放、旋转变化。但这类方法无法准确定位用户指定的特征点，且算法复杂，跟踪速度较慢，不适用于靶场目标实时判读。

基于光流的方法[9]能够通过同名点匹配进行定位，但是靶场图像大多数为天空背景，纹理弱，使得光流特性不明显，且原始的光流类方法无法适用目标帧间的大幅度运动；而基于金字塔光流的方法运算量大，无法满足实时性要求。

核相关滤波算法(Kernelation Correlation Filter, KCF)[10]是一种判别式的跟踪方法，利用目标周围区域的循环矩阵采集正负样本，使用脊回归训练目标检测器，运算速度快，能满足实时性要求。但在无法预测下帧目标位置时只能基于当前位置进行搜索，在目标大幅度的运动下将会丢失目标。

基于模板相关的方法是比较常用的用于特征点跟踪的方法，以特征点为中心生成模板，在后续图像上逐像素进行匹配，找到相似性最大的区域作为跟踪结果。其存在搜索范围与时间性能之间的矛盾：搜索范围越大，耗时越长，且对于弱纹理目标，容易产生匹配错误；而搜索范围较小时，无法应对目标大幅度运动的情况。

由此可知，经纬仪抖动引起的大幅度位移，会额外增加算法的运算开销，甚至导致跟踪失败，因此，研究如何高效地应对由经纬仪抖动引起的跟踪困难具有重要的意义。本文在分析经纬仪综合角度规律的基础上，给出一种结合位置预测和KCF的改进TLD跟踪框架。由位置预测准确给出KCF的跟踪区域，在此区域内进行跟踪。在目标运动速度不发生突变的情况下，可以准确预测目标位置以及目标是否在视场内，使KCF能够快速准确地跟踪目标。在跟踪失败时，采用TLD框架中的检测算法进行检测，同时完成目标特征学习。

1 靶场实时判读方法

1.1 改进的TLD框架

1.1.1 TLD框架

1.1.2 TLD用于实时判读存在的问题

TLD框架在事后长时跟踪上取得了不错的效果，但将其用于实时跟踪时存在以下问题：

1)跟踪采用的金字塔光流法运算量比较大，而检测采用全场逐像素检测的方式同样比较耗时，无法满足实时性的要求；

2)由于目标及背景纹理都比较弱，基于光流的方法跟踪效果不太好；

3)基于全图逐区域检测的方法比较耗时，尤其在目标在图像中占比比较小时，比较浪费计算资源；

4)原始的TLD算法同时进行跟踪和检测，其跟踪结果可信度高，全场检测的意义不大，同样会造成资源浪费。

1.1.3 改进的框架

图1 TLD在线跟踪流程图Fig.1 Flow chart of TLD online tracking

图2 改进后的TLD在线跟踪流程图Fig.2 Flow chart of improved TLD online tracking

1.2 基于综合角度滤波的位置预测方法

1.2.1 观测模型

靶场经纬仪在跟踪时会记录相机光轴的角度信息(即原始角度)，包括方位角和高低角。本文所说的抖动指的就是原始角度的突变。而基于相机内参数、目标在图像上的偏移及原始角度，可以得到光心到目标的指向角，即综合角度。如图3所示，O同时表示坐标系原点和经纬仪的光心，T为目标，OA为光轴，∠xOC为原始方位角，∠AOC为原始高低角，∠xOD为综合方位角，∠TOD为综合高低角。综合方位角和综合高低角统称为综合角度。由于目标运动规律不可能在短时间内产生突变，因此综合角度同样不会产生突变，这也是本文预测算法的基础。

图3 靶场坐标系及角度示意图Fig.3 Coordinate System and attitude angle definition schematic

以单相机观测为例说明本文预测算法的应用场景，如图4所示，由于导弹等目标一般会有预定轨道，可以认为目标短时间内在一个平面内沿某曲线S运动，直线L为目标运动轨迹在地面上的投影，S和L共面。相机部署在目标运动轨迹的一侧，T为目标，C表示经纬仪光心，E为T在L上的垂直投影，E为垂足，CE(即d)表示C到L的垂直距离，h为目标垂直高度，ED(即l)表示目标投影到E的距离。

图4 单相机观测示意图Fig.4 Single camera observation schematic

1.2.2 预测模型

定义角度α和β分别为

α=arctan(l/d)

(1)

(2)

由上述定义可知α和综合方位角∠xOD只存在一个固定差值，而β=∠TOD，因此两者变化规律一致，可以由综合角度的规律分析α和β的变化规律。若h、l、d已知或者有较精确值，也可以由α和β来准确分析综合角度的变化规律。对式(1)求导得

(3)

式中Δl=vt为两帧之间目标水平方向位移量，t为两帧之间的时间间隔，可以由设定速度与拍摄频率得到初始值。以目标速度300 m/s、拍摄帧率25帧/s、d为10 km计算，Δl为12 m，α每帧的变化量约为1 mrad。

由式(2)可得

(4)

由上述分析可得，在目标方向不发生大于90°变化的情况下，Δl的符号保持不变，d为常数，因此方位角呈单调变化趋势。在Δl不变的情况下，当目标位于经纬仪与轨迹的垂足处(即l=0)时，方位角角度变化最快，越远离垂足处则越慢，且关于垂足对称。在目标高度一致的情况下，高低角在垂足处取得最大值，其角度变化曲线类似于抛物线，关于垂足对称。为了更直观地分析其变化规律，通过仿真获得角度变化曲线。具体仿真条件为目标做抛物线运动，速度为250 m/s，经纬仪距离目标轨迹的垂直距离为10 km，拍摄频率为25帧/s，得到综合角度的曲线及其一次差曲线如图5所示。

(a) 角度曲线(a) Angular curve

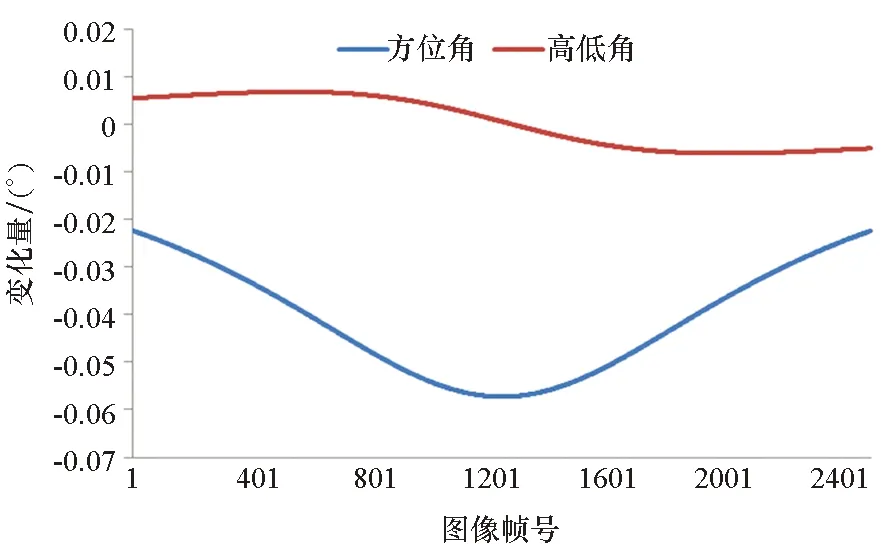
(b) 角度变化曲线(b) Curve of angular change图5 综合角度及其变化率曲线示意图Fig.5 Diagram of integrated angle and its rate of change curve

由仿真结果可知，在匀速直线运动的前提条件下，综合角度均呈连续光滑变化趋势，可以进行曲线拟合。而在一定时间范围内，可以认为目标满足匀速直线运动要求，因此采用曲线拟合预测下一帧的方位角高低角。

由于在实际场景中，l未知，且考虑到经纬仪给出的角度中必定包含一定的白噪声，因此对综合角度序列采用正交多项式最优线性滤波器进行外推[11]，预测下一帧的方位角和高低角，具体外推公式为

(5)

式中，N为滤波窗口，a<0时该公式为内插公式，a>0时该公式为外推公式。当数据量为2时，直接采用等间距外推；当数据量小于N且大于2时，把当前数据量作为滤波窗口进行外推；当数据量大于等于N时，采用最新的N个数据进行外推。本文中N取31。

由上述分析可知，只需初始给出两帧图像的综合角度，本文的预测算法就可以基于前两帧进行预测。

1.2.3 预测位置解算

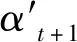
(6)

可求得目标在图像上的预测位置为

(7)

上式中得到的点(x,y)即为在t+1时刻的预测位置。由上述关系式可知：预测角度和原始角度差别越大，则点越偏离图像中心。若点(x，y)位于图像内，则在以该点为中心的图像区域利用KCF进行跟踪；若点位于图像外，则跳过该帧以免跟踪器进行错误的更新。

2 实验验证

通过仿真靶场经纬仪跟踪场景对本文提出的预测算法进行测试，检验本文预测和跟踪算法的性能。 仿真软件环境为：Windows 7 64位专业版，Microsoft Visual Studio 2008；硬件环境为 HP ZBook 17 G3，CPU型号为Intel(R) CoreTMi7-6820HQ 2.7GHz。

2.1 仿真说明

2.1.1 仿真条件说明

本文按照实际任务情况下设备的精度及类似运动轨迹，仿真一组相机参数及目标轨迹，用于验证本文给出的位置预测算法以及跟踪框架，具体参数如下：经纬仪坐标为(1000，2000，3000),等效焦距为62 500,图像分辨率为720像素×576像素，目标从(-1500，8237.5，3500)到(4992，8240，18 494)做抛物线运动，最高点坐标为(-5000，9800，11 000)，拍摄帧率为25帧/s，轨迹长度为100 s(即总共2500帧/s)，仿真过程中不考虑目标的位姿变化。

仿真中主要考虑两种情况：角度误差和偏移量变化。角度误差主要是针对经纬仪给出的实时角度，在实时测量中靶场经纬仪跟踪的精度一般为5～10 s，因此我们给原始角度增加均值为0的随机高斯误差，方差从1～30 s，以验证算法对于角度误差的适用性。偏移量变化主要是针对目标在图像上的抖动量，以模拟经纬仪的跟踪和抖动。实际跟踪中，为了保持稳定跟踪，一般尽可能保证目标在图像中心，因此仿真的目标位置由在图像中心位置上叠加随机运动得到。本次仿真中给目标位置叠加均值为0像素、均方差为2～60像素的随机运动。每隔100帧，选择一帧增加均值为0像素的随机运动，均方差为正常帧的15倍，模拟经纬仪跟踪时的瞬间抖动，大的偏移会直接使目标跳出视场，将目标位置偏移引起的角度变化叠加到原始角度中，仿真图像如图6所示。

(a) 第1帧 (b) 第200帧(a) The 1st frame (b) The 200th frame图6 仿真图Fig.6 Simulated image

仿真的相邻帧目标运动幅度如图7所示(以均方差分别为6像素和90像素为例)。从图中可以看出，目标相邻两帧跳动主要集中在20个像素以内，符合靶场目标运动规律，偶尔的大跳动为模拟实际场景中跟踪过程中相机抖动的效果。

(a) x变化量(a) Variation of x

(b) y变化量(b) Variation of y图7 目标位置变化量示意图Fig.7 Schematic diagram of target position change

2.1.2 算法参数说明

采用KCF、TLD、OpenCV中的模板相关方法(TM)及本文方法进行跟踪，跟踪点为弹尾点，初始模板均为以待跟踪点为中心、半径为40像素×40像素的区域。由于仿真过程中未考虑目标的位姿变化，算法均设置为不更新模板。

下面对各算法设置情况进行说明：

1)KCF用灰度梯度作为目标的特征，扩展区域比例为1.0，即为目标区域的4倍，采用高斯模板，方差σ2为0.25。

2)TLD不考虑尺度变化，即不使用光流金字塔进行跟踪，主要是仿真时未考虑目标的位姿变化，且进行特征点跟踪时不需要考虑目标的整体变化。

3)TM采用全图匹配的方式，匹配方法为归一化平方差匹配法。

4)本文方法中KCF同样用灰度梯度作为目标特征，扩展区域比例为0.5，即为目标区域的2.25倍，同样采用高斯模板，方差σ2为0.25，跟踪失败的比例阈值为3。

2.2 性能评估

2.2.1 预测性能

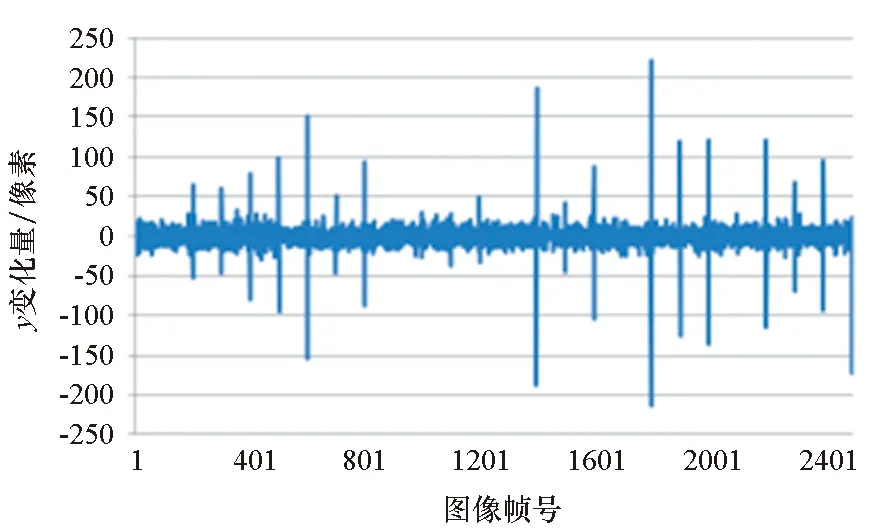
仿真时，根据经纬仪参数和目标在世界坐标系下的位置，给出目标相对于经纬仪的综合角度。预测算法利用前序帧的综合角度及当前帧的光轴角度预测目标可能出现的位置，由于基于窗口的算法无法直接应对相机抖动带来大幅度的位移，因此预测算法的准确性就是基于窗口跟踪算法能否成功跟踪的关键。本文以预测位置与仿真目标实际位置的偏差作为预测算法的评估标准。靶场经纬仪的相机内参数一般需要经过精密标定，误差不大，且由于焦距较长，同样不考虑畸变，因此本文不考虑内参数误差，仅考虑角度误差和目标位置抖动量对位置预测精度的影响。对于每个角度误差和位置跳动量，由于需从第3帧才能进行预测，因此均只计算总共2498帧的预测偏移的均值，同时对预测位置和真值的偏差进行统计，偏差大于60个像素则认为预测失败。经统计预测失败次数为0。预测结果如图8所示。

(a) 预测误差与角度误差的关系(a) Relationship between prediction error and angular error

(b) 预测误差与位置偏移的关系(b) Relationship between prediction error and offset error图8 位置预测算法结果Fig.8 Results of the position prediction algorithm

从图中不难看出，位置预测误差随着角度误差的增大而增大，而与目标偏移无明显关系。这主要是因为角度的偶然误差会直接影响目标位置的解算，但由于采取了滤波算法来抑制角度的随机误差，因此预测误差并没有与角度误差成正比。而目标位置的变化会准确叠加到综合角度中，因此不会引起预测位置的偏差。由此可以证明本文预测算法的有效性。

2.2.2 跟踪性能

图9 跟踪误差与抖动量的关系Fig.9 Relationship between the tracking error and the jitter range

在角度误差和抖动量变化情况下分别用KCF、TLD、TM及本文方法进行跟踪，跟踪结果如图9和图10所示。TLD在目标帧间位移较大时无法给出符合前后帧光流一致性的目标区域，导致跟踪失败，其失败次数随着抖动量增大而增大，而与角度误差无关，图中只给出了跟踪成功时的精度。KCF目标帧间位移比较小时能稳定跟踪目标，但目标帧间位移比较大时就会丢失目标，但在不更新模板的情况下能重现捕获目标。

由图9可以看出，KCF的跟踪误差随着抖动量的增大而加大，而本文方法与全图匹配的模板匹配且与TLD相当，误差平均值在1像素左右，由此可以证明本文方法应对相机抖动的有效性。

图10 跟踪误差与角度误差的关系Fig.10 Relationship between the tracking error and the angle error

由图10可以看出，本文方法在综合角度从1″到30″时，仍然保持与全图匹配和与TLD相当的精度，且优于KCF，能满足靶场实际使用的需求。

2.2.3 时间性能

统计跟踪算法平均每帧耗时，统计结果如表1所示。

表1 跟踪算法耗时Tab.1 Time cost of track algorithm

从表1不难看出，本文方法比KCF和TLD耗费的时间少。与KCF相比，本文算法给出了预测位置，在提高了成功率的同时缩小了匹配的区域范围，因此其耗时相比KCF更少；相比于TLD，本文使用的KCF比金字塔光流法更快，因此在耗时方面远优于TLD；基于全图搜索的模板相关方法耗时最多。

2.3 靶场验证

本文算法已在多个靶场用于实际判读任务，同时也与其他算法结合使用。实际使用情况证明，本文给出的算法在经纬仪抖动时能较准确地预测目标位置，能有效应对经纬仪抖动的情况，减少了抖动时的人工干预，同时能提供目标是否在图像内的信息给其他跟踪算法，从而有效避免跟踪器的错误更新，提高了跟踪算法的鲁棒性。

3 结论

针对经纬仪随机抖动引起的跟踪困难，提出一种融合位置预测、KCF和改进TLD的图像实时判读方法。经仿真验证，本文方法能够根据综合角度准确预测目标出现的位置，提高KCF跟踪的成功率，有效应对靶场经纬仪抖动的情况，每帧仅耗时1.1 ms。经靶场实际使用验证，本文提出的算法能大幅度提高靶场判读的自动化程度，减少人工干预的次数，同时能跟其他基于窗口搜索的跟踪算法有效结合，提供目标预测位置，提高其他跟踪算法应对目标大幅度位移的能力，提高跟踪算法的鲁棒性。