桥墩刚度对曲线桥梁抗倾覆稳定性的影响分析

巩美杰

南京市城市与交通规划设计研究院股份有限公司

1 引言

曲线连续箱梁在城市快速路中，尤其是互通式立交匝道桥中被广泛应用，其下部结构多采用花瓶式独柱墩。自2007年以来，国内相继发生了多起匝道桥整体倾覆事故，造成了巨大的生命及财产损失，引起了社会各界的广泛关注。国内学者针对独柱墩桥梁及类似结构的侧倾问题做了一些研究，研究方法和计算假定得到了逐步发展。初期以“刚体假定”为基础，认为桥梁倾覆破坏时，上部结构绕某一“倾覆轴”做刚体转动。这种方法忽略了箱梁本身作为弹性体的特征，在某种条件下会高估桥梁的抗倾覆能力。文献[2]通过对事故桥梁进行分析，建立了考虑几何及接触非线性的有限元模型，对桥梁倾覆破坏的机理进行了研究，JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》对前述研究做了总结和深化。提出了以“安全系数”表达的抗倾覆验算方法。以恒载产生的“稳定效应”与活载产生的“失稳效应”的比值来衡量箱梁的抗倾覆能力。当为直线桥时，其原理与“刚体假定”理论相同，即“倾覆轴”为偏载侧支点的连线；当为曲线桥时，其“倾覆轴”可以理解为偏载侧支点所构成的曲线。在连续梁设计时很少考虑下部结构对结构的影响，支座常以刚性支点模拟。这种做法在直线桥设计时是可行的，当桥梁为曲线桥时，由于弯扭耦合现象梁体内将产生巨大的扭矩，在横向支座间距较小时，将使曲线内、外侧支座产生反力差。这时若忽略桥梁上、下部的协调变形，计算结果将产生偏差，极端情况下可导致结构的不安全。本文以某互通匝道桥为依托，应用规范提供的抗倾覆验算方法，讨论下部结构对桥梁抗倾覆稳定性的影响。

2 算例分析

某3m×26.5m 预应力匝道桥，宽10.1m，采用单箱双室箱梁，花瓶墩高12m，支座间距2.8m，桥梁位于110m 圆曲线上。本文对是否考虑桥墩的影响分别计算并进行对比分析，计算采用midas civil程序，主梁单元采用7自由度空间梁单元，预应力线形和位置按实际输入，支座与主梁单元间设置刚臂。下图为是否考虑下部结构时各工况支反力计算结果。

分析发现：（1）下部结构对成桥支反力有一定影响，其影响程度与桥墩的刚度有关，刚度越小影响越大。与未考虑下部结构相比，边支点曲线外侧支反力增大，内侧减小；中墩曲线外侧支反力减小，内侧增大。（2）当边支座作为失效支点时，活载支反力差别较大。以1-2支点为例，当不考虑桥墩刚度时，活载在失效墩处产生的支反力较大，远端支点支反力迅速衰减。当考虑桥墩刚度时，远端支点仍能产生不平衡反力。（3）当中墩支座作为失效支点时，活载产生的支反力差别不大。（4）两种模型在以边支点为失效支点计算箱梁倾覆系数时产生较大差别，如表1所示。

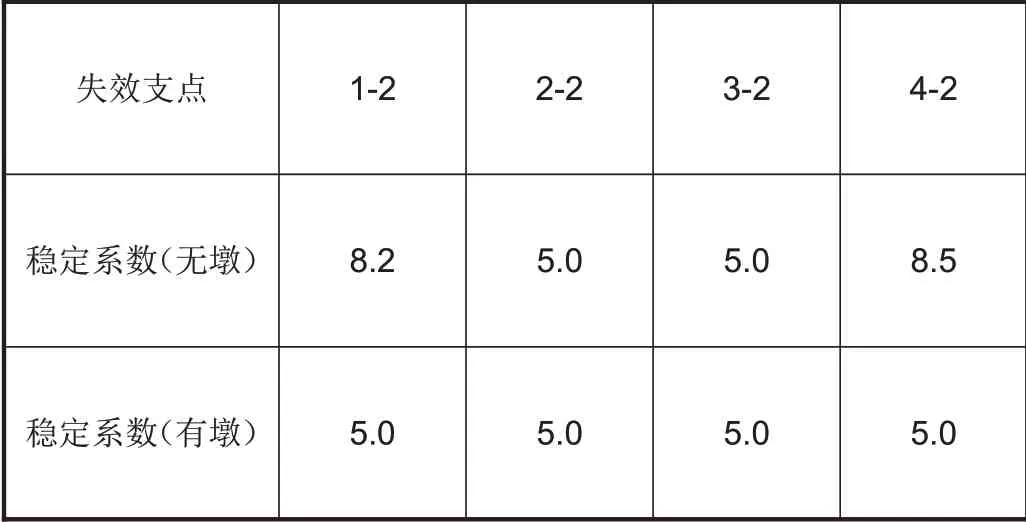
表1 抗倾覆稳定系数比较

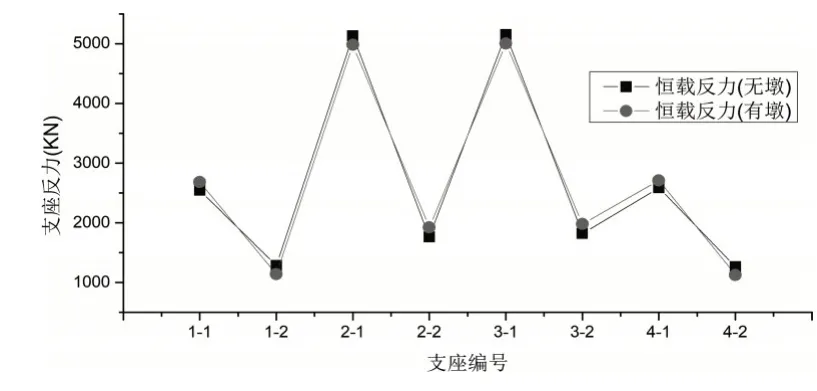
恒载支反力

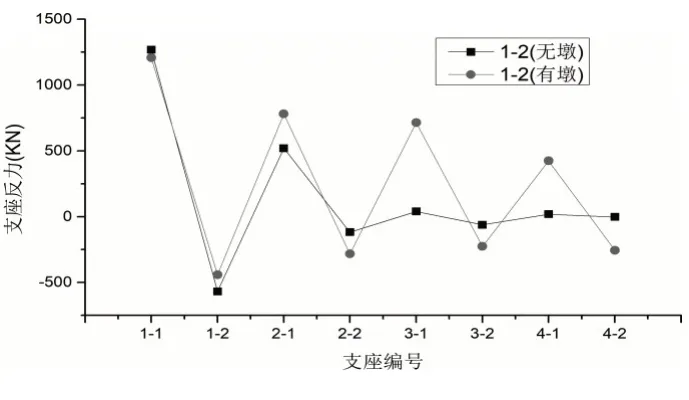
1-2支座失效时活载支反力

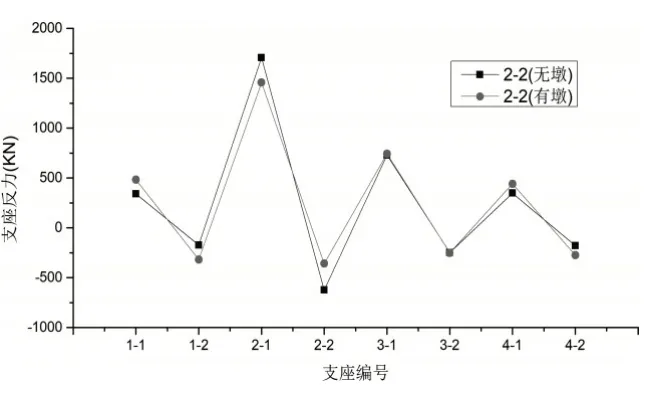
2-2支座失效时活载支反力

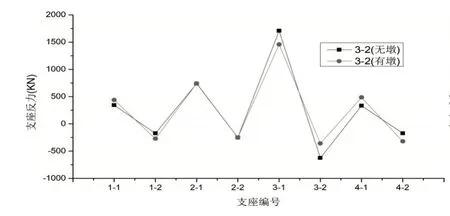
3-2支座失效时活载支反力

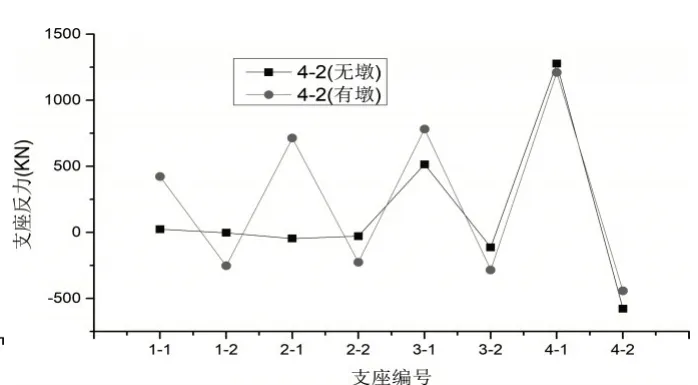
4-2支座失效时活载支反力

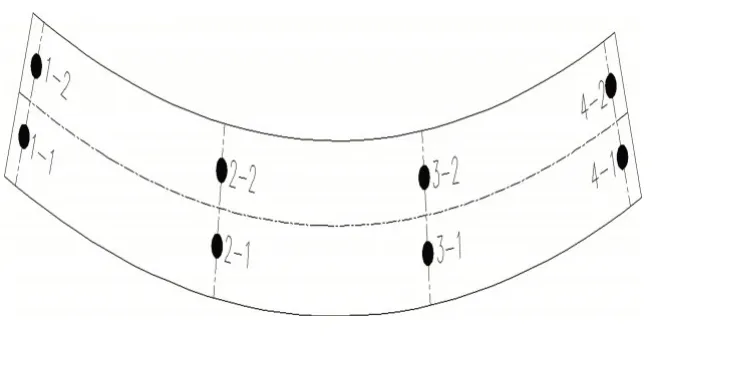
支座编号示意图

通过对活载进行追踪，发现当以边墩支点作为失效支点时，两种模型的反力影响线存在差异，原因在于当不考虑桥墩影响时，支座为刚性支点，限制了梁体的扭转变形，活载的最不利布置范围产生了较大的偏差。当计入桥墩刚度影响时，桥梁上、下部结构协调变形，最不利状态也更符合实际情况。以此推断，当连续梁分跨越多时，若不考虑下部结构影响，最不利活载布载是失真的，其抗倾覆安全性可能被高估。

3 结论与问题

本文通过计算，对比分析了曲线梁桥在是否考虑下部结构影响时，成桥反力及活载反力的差别，并按规范提供的方法得到了箱梁抗倾覆安全系数。

（1）证明曲线桥梁在进行抗倾覆安全性验算时，应按实际情况考虑桥梁下部结构的影响，使上、下部结构变形协调。否则在特殊情况下可能高估箱梁的抗倾覆能力。

（2）因篇幅限制本文仅对三跨连续梁进行了分析，当连续梁跨数增加后下部结构对抗倾覆验算的影响将会增大为作者推测，待后续研究论证。

（3）连续梁倾覆验算实质是寻找“失稳效应”极值的过程，规范将其进行了简化，即认为“失稳效应”的极值为同侧各支点达到最小反力时的包络值。这种简化在跨数较少时是安全的，但当分跨较多时是否存在“漏载”问题，有待后续研究。