Statistics matters in interpretations of non-traditional stable isotopic data

Abstract Increasing volumes of of non-traditional stable isotope data have brought new opportunities to gain important insights into geochemical and planetary processes. However, there is a worrysome trend that the isotopic data are interpreted in a fashion that its statistical approaches are chosen subjectively. This communication summarizes the rules regarding calculating the mean,standard deviation and relative standard deviation of a population, as well as error propagation and significant digits. These rules should be used when reporting geochemical data, especially for isotope ratios. Using two examples, I show that statistics matters in isotopic data interpretation.

Keywords Isotopic data processing · Error propagation ·Significant digits · Difference between means with uncertainties

1 Introduction

Geochemistry requires precise and accurate analyses of natural and synthetic samples. The ability of geochemistry to reveal planetary and geological details is largely limited by instruments and analytical approaches to extracting the information, especially element abundances and isotope ratios.Since the 2000s,the two aspects have received great attention from the community and yielded high-quality data that successfully provide more information for the formation and evolution of Earth, Moon, Mars and other members in the Solar System. However, two important issues concerning the correct presentation of geochemical data are sometimes ignored: error propagation and significant digits.These are the basics for statistical treatment of data which is worthy of serious attention.In this paper,the two issues are discussed in the following sequence: (1)calculations of mean, standard deviation (σ), and relative standard deviation (RSD) of different steps for a normal geochemical data set; (2) error propagation; (3) significant digits; and (4) examples of published geochemical data.

2 Calculations of the mean,σ,and RSD in the raw data processing

Currently, element abundances and isotope ratios of geological samples are generally measured by mass spectrometers, including inductively coupled plasma mass spectrometer (ICP-MS), multi-collector inductively coupled plasma mass spectrometer (MC-ICP-MS), thermal initialization mass spectrometer (TIMS), and laser-equipped mass spectrometers like LA-ICP-MS and LA-MC-ICPMS.Regardless of the types of instruments,the fundaments of their reporting geochemical data are similar (Table 1).

A stable particle flow from a sample should be formed and transported through the mass spectrometers;ion counts or electricity produced by ion bombarding Faraday cups have to be accounted through several cycles. Due to instabilities of instruments, ionization or introduction systems,ion counts or electricity of these cycles naturally varyin a certain range,which is called instrumental uncertainty.This uncertainty is translated into uncertainties (σCand RSDC) of the mean (CMean) element abundance or isotope ratio of the cycles. In geochemistry, it is rare to just measure the sample once; therefore, several measurements of the same sample yield a mean of measurements (MMean)and its uncertainties (σMand RSDM). Because of the potential heterogeneity of geological reservoirs, geochemists generally tend to measure several samples from the same reservoir to obtain presentative values(SMean,σS,and RSDS) which are compared with other geological reservoirs. It is unavoidable that error of each former step will be propagated to the next step and these errors are all reflected in the report of the final number.

The old woman followed the goat into the cave and then, what should she see but the animal giving her milk to a little boy-baby, whilst on the ground near by lay the sad remains25 of the baby s dead mother! Wondering and frightened, the old woman thought at last that this little baby might be a son to her in her old age, and that he would grow up and in time to come be her comfort and support

3 Error propagation in the raw data reduction

Errors(σ or RSD)of the calculations in Table 1 are always inevitable. Therefore, it is important to combine the errors from different steps (http://www.physics.umd.edu/courses/Phys261/F06/ErrorPropagation.pdf). In a more universal sense,the exact formula of random error propagation is the following equations.

where x is the end result; a，b，c are independent random variables.

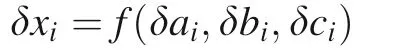
where δxiis the uncertainty of the ith of x;δai，δbi，δciare uncertainties of a，b，c, respectively.

Therefore,the total deviation δx of x is derived from the individual deviation of x concerning each of the variables:

The standard deviation of x can be calculated from the following steps.

Memories help, too. Muriel stocked the cupboard of my mind with the best of them. I often live again a special moment of love she planned or laugh at some remembered outburst of her irrepressible approach to life. Sometimes the happy doesn t bubble up with joy but rains down gently with tears. In the movie Shadowlands, when Joy Gresham reminds C. S. Lewis that their joy would soon end, that she would die, he replies that he doesn t want to think about it. Joy responds, The pain is part of the happiness. That s the deal.

First, squaring the individual deviation of x concerning each of the variables:

In order to cancel some variables, the cross-terms are needed:

Assuming there are N measurements, then the standard deviation equation is:

All this time the young man was riding through the world, and when the seven years and seven months were over he came back to the town where the princess lived--only a few days before the wedding

because

Digits of the results(element abundances or isotope ratios)after error propagation are viewed as degrees of precision of the present work. Therefore, a current tendency in geochemistry, especially isotope geochemistry,is to report many digits if possible as measurements and analytical approaches are improved. However, the determination of significant digits is not well understood in a large portion of geochemistry communities. Here the statistical grounds and rules that determine the significant digits of the end result are presented based on two lectures (http://www.physics.smu.edu/cooley/phy1308/sigfigs.pdf; http://chem class-ol.org/significant-figures/).

In other tales of the Children and the Ogre Aarne-Thompson classification, the children do not necessarily encounter a witch. The villain104 may be a giant, ogre, or other monster. You can read more on the Tales Similar to Hansel and Gretel page.Return to place in story.

For common calculations, the simplified equations of propagating errors are given in Table 2.

Table 2 Formulas of propagating random errors in common calculations

3.1 Significant digits in data reporting

Therefore the exact formula for error propagation is:

3.2 Significant digits in reading scales

From a very common starting point, reading values of a graduated cylinder with scales of 0.1 mL (1 mL l is separated into 10 portions and marked by shorter lines) filled with a certain volume of liquid (Fig. 1a). Assume that the concave meniscus of the liquid is higher than 6.5 mL but lower than 6.6 mL. One could report the volume to be 6.66 mL, where the last digit ‘‘6’’ is an estimate (it could also be ‘‘4’’, ‘‘8’’, or other single-digit numbers depending on whether the concave meniscus is estimated to be higher than the middle line between 6.5 and 6.6 mL).However,in the case of a 25 mL cylinder with 1 mL as 1 scale(Fig. 1b), the same amount of liquid would be between 6 and 7 mL.One could report 6.6 mL with the last digit‘‘6’’being an estimate. In the above examples, the significant digits are determined by the precision of the measurement may achieve. The philosophy should be equally effective for other conditions.

3.3 Significant digits in mathematical calculations

In this case, the first operated part is 15 ＋5 = 20 with two significant digits, while 10.0 has three significantdigits.Therefore,referring to Rule 2,the final result should be reported as 2.0.

Fig. 1 Examples for reading volumes in cylinders of different scales(Modified from Skoog et al. 2013)

Rule 1 for addition and subtraction: the calculated values cannot be more precise than the least precise quantity involved in the calculation. For example:

2.135 ＋7.2 ＋3.14 = 12.475 (the direct calculated value)

This means that the number of digits of the mean after decimal should be equal to that of σ (standard deviation).For instance as shown in Table 3, if the mean (stable isotope composition) of a sample is calculated to be 0.123,while its standard deviation (σ) is calculated to beHere the σ should be limited to the first non-zero number,0.02,because the number (3) after the first non-zero digit(3) is smaller than 5. Then the value should be reported as 0.12 ± 0.02. However, if the σ were calculated to beconsidering the number (7) after the first non-zero digit is higher than 5, then the final report of the value should be 0.12 ± 0.03. It should be emphasized that how many digits of the mean should be given after decimal is controlled by the number of the first non-zero digit of σ after the decimal,but the exact value of the least significant digit of the mean and 2SD depends on the number after the least significant digit.For instance,as shown in Table,both 0.andshould have two digits after decimal as controlled by their σ,but the final report ofshould be 0.13because the number of the least significant digitis higher than 5.

As animals, and in turn their fur, often represent the carnal nature and physical acts, Donkeyskin is essentially donning the disguise of what she is trying to escape. The skin can also represent the violations76 and sin of which she has been a victim.Return to place in story.

The difference(μ)of weighted means with a confidence interval (CI) of two groups (e.g. A and B) of rocks representing reservoir s can be used to test whether the reservoirs are truly statistically insignificant. As presented in Hatcher (2013), if μA-B= 0 it can be stated that the difference between two reservoirs are statistically insignificant (Case 1 in Table 4 and illustrated in Fig. 2a);if μA-B≠0, the differences between reservoirs isstatistically significant(Case 2 in Table 4 and illustrated in Fig. 2b).

Rule 2 for multiplication and division: the number of significant digits of the calculated value should be the same as that of the quantity with the fewest number of significant digits. For example:

30.59 × 20.6 × 1.3 = 819.2002 (the direct calculated value)

In this case, the quantity with the fewest number of significant digits is 1.3 (two digits). Therefore, the final answer should be reported as 8.2 × 102(820 has three significant digits).

Rule 3 for combined calculations:the significant digits are determined by the order of mathematical operations.For instance:

(15 ＋5) ÷ 10.0 = 2 (the direct calculated value)

From this point of argument, we present three rules that could be used to determine the significant digits in calculations.

Table 3 Examples of reporting digits of the mean (stable isotope composition, ‰)

3.4 Digits in statistics

Returning to the digits of the mean and SD of a population,the following rule is: the last digit of the mean after the decimal is the same decade as the first non-zero digit in the σ (Taylor 1997; Skoog et al. 2013).

In this case, the least precise quantity is 7.2 with the fewest number of significant digits after the decimal point(i.e., one digit number ‘‘2’’ here). Therefore, the final answer is 12.5 that has the same number of significant digit(s) after the decimal point as the quantity with the fewest number of digit(s) after the decimal point.

One day the king came into the stable, where there was no one present except the youth, who said straight out to him that, with his majesty s permission, he wished to ask him why he was so sorrowful

However, it should be pointed out that the digits of the mean are also controlled by units. For instance, there 70 people in group 1, 65 in group 2, 56 in group 3, then the people per group (the mean) isstatistically. But since there is no such thing aspeople, the mean should be reported as 64 using the rounded up rule.

4 Weighted mean and 95 % confidence interval

Several criteria, e.g. standard deviation (σ), standard error(se), and confidence level (cl), can describe relationships among terrestrial bodies. In a geochemical sense, σ is normally useful to show the reliability of the several runs of isotopic ratio measurements of an individual sample. It can also portray the variation of the mean value of large numbers of samples from a single and uniform reservoir.se can serve for the same purpose. Both proxies function better for large sample sets than smaller ones.If the sample quantity is less than 20, one has to consider the weighted average with σ calculated from a certain confidence interval,for instance,95 %.As shown in geochronology,it is a useful tool in data comparison. The basic equation of weighted mean can be expressed as:

where ∑denotes the sum,σiis the standard deviation,and x is the individual value. The smaller the σi, the more weight the xiaccounts for (http://www.physics.umd.edu/courses/Phys261/F06/ErrorPropagation.pdf). By using weighted mean with 2 σ¯x, which roughly equals to 95 %confidence interval, it is possible to distinguish statistical differences among datasets representing different but respectively uniform geologic reservoirs.

I was puzzled! Why was this old woman making such a fuss about an old copse（，） which was of no use to anybody? She had written letters to the local paper, even to a national, protesting about a projected by-pass to her village, and, looking at a map, the route was nowhere near where she lived and it wasn t as if the area was attractive. I was more than puzzled, I was intrigued1（） .

The newly published data of V isotope compositions of lunar samples from Hopkins et al. (2019) is shown as an example where the rules of significant digits should be considered. The corrected results are as the font bold data in Table 5 and the original reports are in normal font.

Table 4 Examples of calculation of μ based on 95 %CI

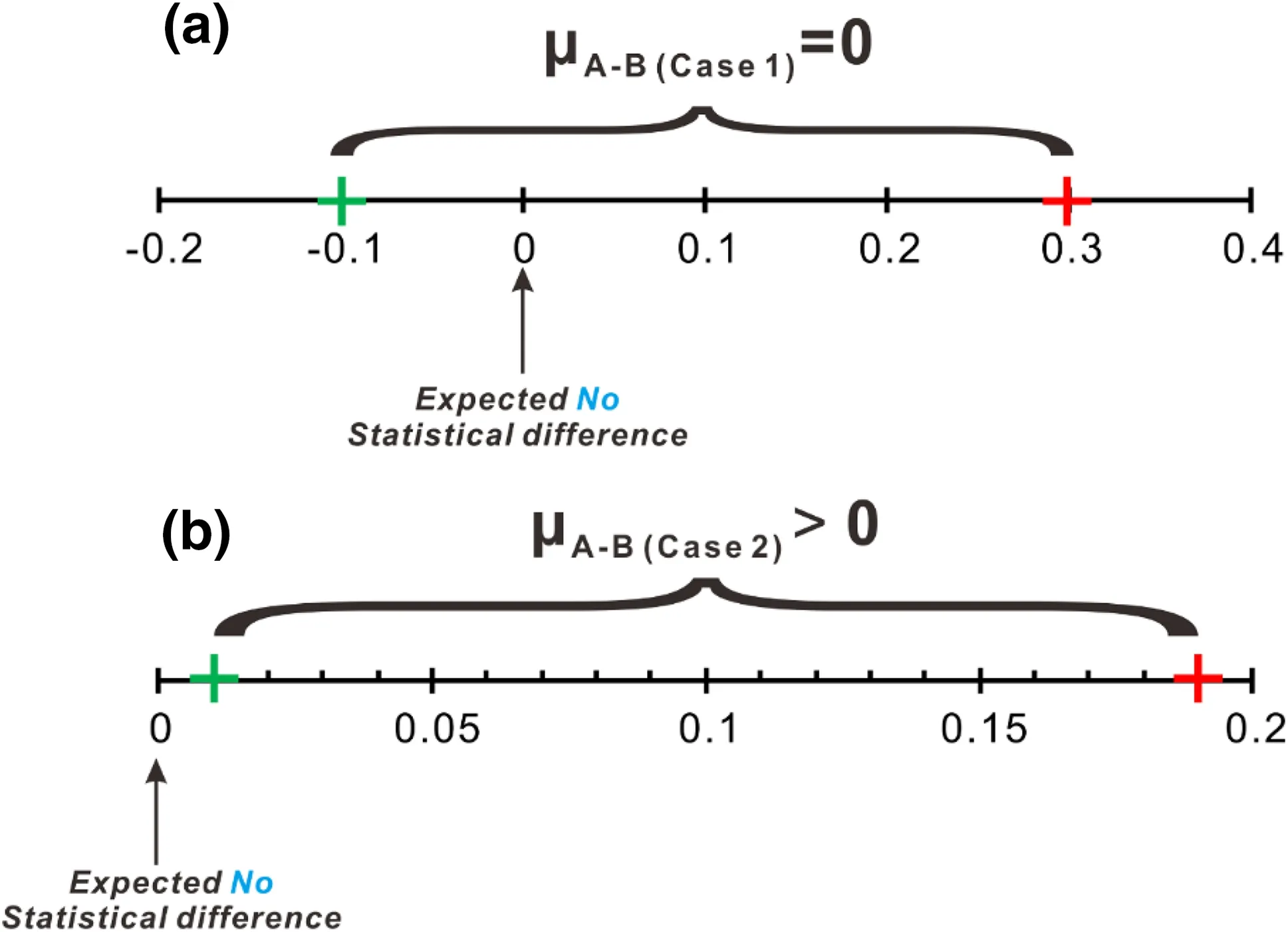
Fig. 2 Using the difference between weighted mean with 95 %CI to evaluate whether two populations are statistically significant. It is an illustration of Table 4

However, as emphasized in Hatcher (2013), μA-Bonly describes whether the difference between two reservoirs is above seriously in order to have a better understanding of geological processes.

5.1 Reporting isotope ratios considering significant digits

18. A great deal of money, and they betrayed the secret to her: Money often brings about corruption. Bribery, especially with money, is found often in literature, even some fairy tales. One of the most famous betrayals in history is Judas Iscariot s betrayal of Christ for 30 pieces of silver in the New Testament.Return to place in story.

Mother sighed as she listened to the latest argument coming from the living room. With Christmas only a month away, the McDonald house seemed sadly lacking in Christmas spirit. This was supposed to be the season of sharing and love, of warm feelings and happy hearts. A home needed more than just pretty packages or twinkling lights on the tree to fill it with the Christmas spirit. But how could any mother convince her children that being kind to each other was the most important way top get ready for Christmas.

Followingthe rule for digits of the mean (Sect. 4.2),it is clear that 2σ can only have one digit after the decimal point where the first non-zero digit is. As the digits of the mean after decimal should be equal to that of 2σ,the mean should also be reported with only one digit after the decimal. Using the correct way of reporting significant digits also changes the mean and the standard deviation of the mean for a certain type of samples, because of error propagation (the first equation in Table 2). Take the High-Ti basalts in Table 3 as an example, the 2 standard deviation of the mean should be calculated as:

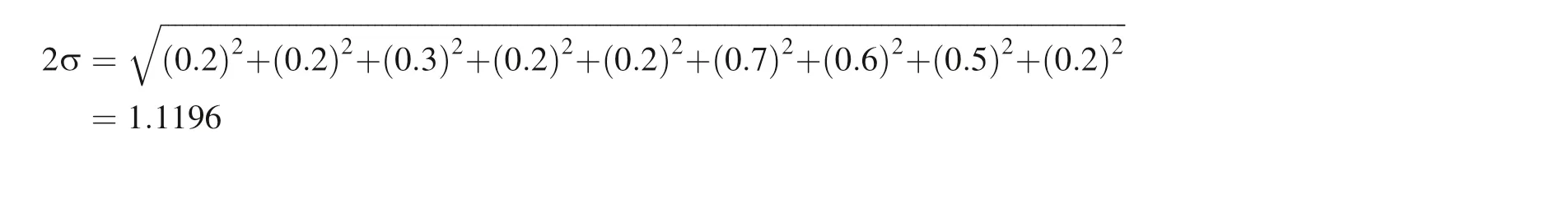
statistically significant, and the μ itself does not represent the true difference between the reservoirs or sample sets.where the first 1 is the first non-zero digit. But the individual sample has two significant digits, therefore the 2σ should be reported as 1.0.

The mean of High-Ti basalts is:

5 Examples of published geochemical data

I present the above summary mainly aiming to re-evaluate some of the reported geochemical data, especially element abundances and isotope ratios. The examples chosen here are not meant to devalue the quality of these papers,but to show that incorrect data expressions could lead to incorrect arguments and conclusions in relevant papers. Therefore,we suggest the community to take the rules discussed

Considering the digits of 2σ after the decimal,the mean of High-Ti basalts should be - 2.0. Therefore, the final report of V isotopes of average High-Ti basalts should be δ51V = - 2.0 (‰) ± 1.0 (‰). Although correcting the reports of δ51V in Hopkins et al.(2019) does not influence their discussions and conclusion, the large 2σ of both individual samples and averages of certain types of samples will likely introduce large uncertainties for their calculation of δ51V of the bulk silicate Moon (BSM). With alarge 2σ for the δ51V of BSM, the difference of δ51V between the BSM and the bulk silicate Earth(BSE)may be underestimated.

The girl stood still before the wonderful plant, for the greenleaves exhaled5 a sweet and refreshing6 fragrance7, and the flowersglittered and sparkled in the sunshine like colored flames, and theharmony of sweet sounds lingered round them as if each concealedwithin itself a deep fount of melody, which thousands of years couldnot exhaust. With pious8 gratitude9 the girl looked upon this gloriouswork of God, and bent10 down over one of the branches, that she might examine the flower and inhale11 the sweet perfume. Then a light broke in on her mind, and her heart expanded. Gladly would she have plucked a flower, but she could not overcome her reluctance12 to break one off.

Table 5 V isotope compositions of lunar samples from Hopkins et al. (2019)

5.2 Calculating true isotopic differences among reservoirs

The higher the precision, the better the resolution.Therefore, scientists put endless efforts to facilitate analytical procedures and thus to improve data quality,hoping to bring more details to light. The best precision of isotope data is ± 0.010 ‰ (2se) which resolves the magnesium (Mg) isotopic difference among chondrites,Earth, Mars, and the Eucrite (Hin et al. 2017) (Table 6).The high precision allows the authors to argue for volatile loss leading to depletions of24Mg relative to25Mg during planetary formation.However,this might be an artifact: the statistical differences using S.E.M.(Standard Error of Mean) do not represent the true difference.

This is because the standard error of mean quantifies uncertainty in the estimate of the mean and it decreases with increasing numbers of measurements (Glantz 2002;Hatcher 2013). Furthermore, the way of Hin et al. (2017)calculating the S.E.M. of the Mg isotope composition of chondrites requires the assumption that these chondrites were derived from a common and homogeneous solar nebulae source with a specific Mg isotope composition(notes of Table 6). Studies on other non-traditional stable isotopes, however, suggest otherwise. Here the interest lies knowing the variability of data from the estimated mean not the proximity of mean to the population mean. In other words, isotope geochemists are generally interested in calculating the mean and its variability of samples representing a certain reservoir and not the precision(S.E.M)of the estimate of the mean based on certain samples of a reservoir.

The true difference is better represented by the difference between means ± 2 standard deviations (2SD or 2σ)where 2σ describes the dispersion of data from mean and it does not decrease with increasing numbers of measurements (Barde & Barde 2012). In this sense and error propagation considered,Earth has an average δ25/24MgDSM-3 = - 0.12 ± 0.09 ‰ (2SD) whereas the chondrites has an average δ25/24MgDSM-3= - 0.1 ± 0.1 ‰ (2SD)(Table 6). Consequently, the true difference Δ25/24MgEarth-Chondritesis- 0.21 to 0.17‰(Table 7),0.02 to 0.05‰as calculated based on S.E.M as in Hin et al. (2017). This strongly suggests that although it is shown the Mg isotope compositions of chondrites and Earth might be statisticallydifferent,the true difference itself cannot be revealed from the current study because of the large variation of Mg isotope compositions displayed by chondrites. This also indicates that the Solar system does not have a uniform and specific Mg isotopic value, theoretically rejecting the approach used by Hin et al.(2017).Analytically,the longterm 2 standard deviation (2σ) of Mg isotope measurements on individual samples should be much lower than the current precision in order to calculated the true difference of Mg isotopes between Earth and an average solar composition (if there was)based on chondrites and thus to constrain the effect of volatile loss of Mg during Earth accretion.

This delighted the greedy Tanuki, who said that they would be no weight for him, so they collected the large branches, which the hare bound tightly on his back

Table 6 Mg isotope compositions of chondrites and Earth rocks from Hin et al. (2017)

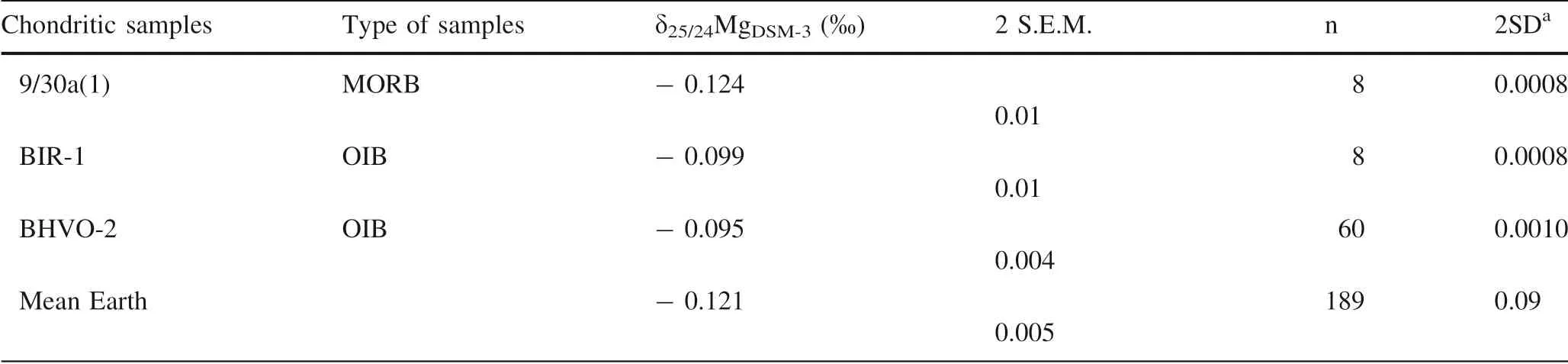
Table 6 continued

Table 7 Mg isotopic difference between Earth and chondrites calculated from mean ± 2SD

6 Conclusions

Applying the rules introduced here to two examples on isotope data, it is shown that statistics matters in isotope geochemistry, especially for interpreting isotope data with high precision and searching for geological or planetary implications. Additionally, although the precision of isotopic measurements have improved, both examples show that better precision is required to distinguish the differences of interested samples representing important planetary and cosmochemical reservoirs.

AcknowledgementsI appreciate the correction from Wangye Li for the manuscript. Anonymous reviewers have greatly improved the quality of the work. This work is financially supported by NSFC No.41703019.