以形解数、寓数于形、形数结合——谈解决问题的策略

梁秀榕

(福建省福州市湖际小学 福建 福州 350000)

数学思想方法是数学科学的灵魂，而“数形结合”思想是一种通过“数”与“形”有机结合，数学知识和数学思想方法两者是相辅相成，密不可分的。因此，在课程标准理念的指导下，作为数学思想成员之一的“数形结合”生动形象的图形使得抽象的知识变得趣味化，直观化，让学生在学习时，不再感到枯燥乏味，反而获得有趣的情感体验，有效培养学生逻辑思维能力，下面就谈一谈“数形结合”这一有效的数学思想方法在教学上的应用。

1.以“形”助“数”，妙解填空

数形结合是根据数量与图形之间的关系，通过“以形助数”和“以数解形”使复杂问题简单化、抽象问题具体化，从而解决数学问题的一种重要的思想方法。六年级上册开始我们经常会见到这样的题目“甲数比乙数多几分之几？那么，乙数比甲数少几分之几？”这类型的题目，由于题中的数量关系比较抽象，因此给学生解题带来一定的难度。

2.以“形”启“数”，巧解问题

数形结合其实质是将抽象的数学语言转化为直观图形，使抽象思维和形象思维结合起来，化难为易，化抽象为直观。以“形”启“数”，即把题目中的数量关系转化成图形，将抽象的数量关系形象化，再根据对图形的观察，分析、联想，一步一步转化成算式，强化对题意的理解，从而达到解决问题的目的。

2.1 利用画图解决问题。如“植树问题”例题：“同学们在全长20米的小路一边植物树，每隔5米栽一棵(两端要栽)一共需要准备多少棵树？

一个间隔一棵树这样画图，清楚直观的可以得出树比间隔多1，所以得出算式：20÷5=4(个)4+1=5(棵)进一步的学习得可以总结出“植树问题”问题的三种情况：

两端都种：棵数=间隔+1

一端栽种：棵数=间隔

两端都不种：棵数=间隔-1

利用图形帮助学生学习，让学生得到凭借工具，借助数形结合将文字信息与学习基础结合，使学习得以继续，使学生思维发展得以凭借，也使得数学学习方法真正得以渗透。

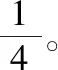
运用“数形结合”的方法，不仅使知识通俗易懂，学生易于接受，而且在数学思想方法的熏陶下，学生对数学更感兴趣，从而能够举一反三，自主探究。“数形结合”思想广泛地渗透在小学数学教学中，因此，教师要深度挖掘教材，在教学过程中有意识地巧妙运用，让学生更好地掌握这一方法。同时也应该注意不要过于夸大“数”或者“形”的作用，应从整体上把握二者之间的关系，“数”与“形”应有机结合，相辅相成。在课堂中，充分发挥教师的主导作用和学生的主体地位，让学生在主动建构、自主探索过程中自觉地运用这一思想，就能“变学生学会为会学”，提高学生的数学素养，在数学教学中真正实现素质教育。