随机变量数学期望的教学实践与探索
2020-05-05丁黎明
丁黎明
(江苏财会职业学院 基础部,江苏 连云港 222061)
随机变量数学期望在概率论与数理统计理论中是一个极为关键的数字特征,对于离散型随机变量的分布、连续型随机变量的分布、随机变量函数的分布、矩概念、参数的矩估计等问题中都会涉及到数学期望,因此数学期望在概率统计中占据着重要的地位,发挥着重要的作用。[1-2]由于随机变量数学期望在离散型随机变量、连续型随机变量、随机变量函数中表达形式的变化导致其具有不同的计算公式,学生对这些公式较难理解并且容易混淆,特别是在计算随机变量函数的数学期望及参数的矩估计方面更为突出。教师在教学过程中应从数学期望的现实意义出发,注意把握数学期望的概念,利用案例教学法帮助学生理解概念,区分公式,正确运用。
1 用实际案例引入数学期望的概念
1.1 创设情景案例
通过创设实例,引导学生观察、探索、发现,培养学生的综合分析能力。
例如,观察甲乙两名射手10次射击的成绩如下表:

甲中靶环数58697820510乙中靶环数7857565566
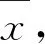
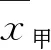
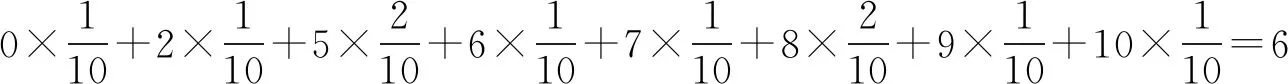
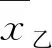
1.2 引导启发学生
(1)由此可得甲乙两名射手的平均射击水平相同,相应地即为观察到的平均中靶环数。
(3)当射击次数增多时,频率的稳定值为概率,即平均射击水平表示为中靶环数乘以相对应的概率之和。
(4)抛去实际意义,抽象出变量取值的平均水平,可得数学期望的概念。
1.3 总结归纳概念
1.设离散型随机变量X的概率分布为
P{X=xk}=pk,k=1,2,…
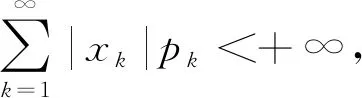
对于连续型随机变量X,设其概率密度函数为f(x),其数学期望的定义可参考离散型情形的定义,转化为离散型情形的近似并利用定积分知识来推导。
2.设连续型随机变量X的概率密度函数为f(x),若积分
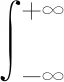


概率论与数理统计中关于随机变量的另一个数字特征方差,以及多维随机变量数字特征的协方差,这些概念都是建立在数学期望的基础上进一步深入发展,数学期望能够更为直观、更为形象地反映出这些抽象的概念。因此,弄清楚数学期望在这些问题中的作用,对于学好随机变量的数字特征尤为重要。
2 用生活背景激发学生的学习兴趣
作为概率统计的一个概念,数学期望可以在日常生活中的很多方面寻找到多种类型的数学模型,在一些实际问题中,人们往往并不需要全面考察随机变量的变化情况,而更关心的是随机变量的某些特征。在讲授这一概念时教师可以运用课内课外相结合的方式,提高学生的理解能力和运用能力。例如,让学生利用网络、论坛、图书等途径寻找搜集关于数学期望的一些实际问题,并加以讨论。通过这种方式可以让学生自己亲身参与教学实践中,使学生对数学期望基本概念、基本知识的理解更为深刻,提高学生灵活运用数学知识解决生活实践活动的能力,进一步激发学生的学习兴趣。[3]
例如,某人每天早上从家出发步行去上班,途中经过3个红绿灯路口,假设在各红绿灯路口遇到红灯的事件相互独立且概率都是0.4,若遇到红灯需要等候5分钟。问此人平均每天早上上班遇到红灯需要等候的时间是什么?
分析:设X是此人每天早上上班途中遇到的红灯次数,可知X~B(3,0.4),则

从而X的分布列为
于是,遇到红灯的平均次数为E(X)=0×0.216+1×0.432+2×0.288+3×0.064=1.2,故此人平均每天早上上班遇到红灯需要等候的时间是5×1.2=6分钟。
3 用案例教学提高学生的应用能力
数学期望的实际意义表示随机变量取值的平均水平,教师可以从实际问题的意义出发,通过给学生提供案例材料,引导学生对指定的案例内容进行思考分析,再向学生提出与内容有关的平均值问题,使学生尽快进入案例内容的情景,弄清案例当中的因果关系,寻找解决平均值问题的方法途径,因此案例教学的思想方法得到了充分的体现。比如评定某班级的成绩水平情况办法:考察各班级的平均成绩,若某个班的平均成绩最高,则认为该班的成绩好;评定某市区居民的家庭收入情况办法:考察各家庭的年平均收入,若某个市区的家庭年平均收入最高,则认为该市区居民的家庭收入高,相应地该市区居民的生活水平高。类似的还有某校学生的身高、体重情况,测量的平均误差、产品的平均质量指标等。当然数学期望的应用也可以延伸到其它的学科领域,如自然科学、工程技术、经济管理、法律、医学、体育等诸多领域。
案例教学法具有实践性强的特点,有利于把抽象的问题具体化,激发学生学习的兴趣,提高学生学习的主动性和积极性。[4]通过案例教学实施过程,最大程度调动学生互动学习。
在教学中案例教学法是教师常用的一种教学方法,一是有助于学生理解接受所要学习的问题,通过案例让学生直观而具体地面对问题,使学生将抽象的问题具体化,从而聚焦要讨论的问题。二是有助于提高学生分析问题、解决问题的能力,运用案例进行数学期望的教学过程,使学生运用案例所代表的实际意义进行深入细致地分析,解决案例当中的各种问题,学生可以充分发挥自己的主动性思维,进而结合案例找出合适的解决办法。三是有助于提高学生实际应用的能力,教师选取的案例通常是贴近学生的日常生活或工作实际,目的是增强学生的吸引力和互动力,能够促使学生综合运用所学的知识,促进学生将所学的知识迅速转化为应用的能力。
4 用课程思政培养学生的爱国情怀
课程思政是把思想政治教育融入课程教学,构建三全育人格局的形式并与思想政治理论课程同向同行,在课堂教学过程中落实立德树人的根本任务。把课程思政理念融入到教学过程的各个环节,是加强新时代思想政治教育的基本途径,也是贯彻和落实习总书记讲话精神的重要举措。各类课程要结合其自身特点,收集大量典型案例,循序渐进融入课程思政,实现课程思政和思政课程同向同行,协同育人。在数学教学中融入课程思政理念,推动文化素质教育与思想政治教育紧密结合。
在讲解数学期望的概念时可以多举实例,让学生理解数学期望的实际意义,这是进行课程思政的有利时机。比如选择我国的“十三五”规划脱贫攻坚,实施精准扶贫政策。根据地方特点发展特色经济,提高贫困地区经济收入,减少贫富之间的差距,全面打赢脱贫攻坚战,提高全国人民平均生活水平,逐步实现共同富裕的总体目标,这里“平均生活水平”就是全国人民生活水平数学期望的具体意义。在教学中,还可以让学生自己利用数学期望的实际意义解读脱贫攻坚政策,分析脱贫攻坚政策背后的数学概念,建立两者之间的有机联系,使学生更好地理解国家的大政方针政策,感受我国社会主义制度的优越性,弘扬社会主义核心价值观,增强四个自信。
5 用拓展问题加深学生的知识理解
设计以下问题有助于学生掌握数学期望的概念、公式、性质及与相关内容的联系。
思考问题一:随机变量数学期望的基本类型有几种?
由于概率论与数理统计主要讨论离散型与连续型两种类型的随机变量,在教学中,教师必须强调随机变量数学期望的基本类型也是划分为:离散型随机变量数学期望与连续型随机变量数学期望。
思考问题二:随机变量数学期望的计算公式有几种?
随机变量数学期望的计算公式有两种:
(1)离散型随机变量数学期望计算公式
(2)连续型随机变量数学期望计算公式
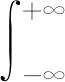
思考问题三:对任意常数a,Ea=a吗?
从数学期望的意义分析,数学期望表示随机变量取值的平均值,而任意常数的平均值还是该常数。
思考问题四:数学期望与方差的关系?
数学期望表示随机变量取值的平均值,而方差DX=E(X-EX)2反映随机变量偏离其中心的离散程度,即相对于数学期望的平均偏离程度。数学期望是衡量随机变量偏离的中心,也是方差计算的基础。
思考问题五:如何理解随机变量函数的数学期望?
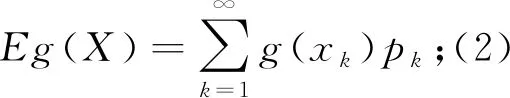
思考问题六:数学期望与矩的关系?
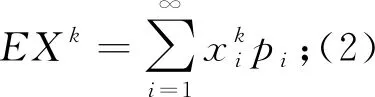
6 结语
数学期望是随机变量的重要数字特征,从教学内容中去挖掘所蕴含的思想方法,教师在整个教学中要精心设计教学过程,积极引导学生主动参与教学环节,共同创设师生教学互动,努力培养学生科学探究的思想意识和数学学习能力,全面提高教学效果。
