光栅尺位移测量系统热态特性分析
2020-05-04胡发伟张文涛熊显名
胡发伟,张文涛,熊显名,杜 浩
(桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004)
0 引言
随着科学技术的进步与发展,对产品加工和工业技术要求的精度越来越高,高精度测量技术越来越受到重视。作为集成电路制造的核心装备,光刻机决定了集成电路的特征尺寸和集成度。运动台(掩膜台和工件台)的位置测量直接影响光刻机三大性能指标中的产率和套刻精度[1]。上海SMEE公司正在研制的28nm浸没式光刻机代表了国内最高水平,其掩膜台套刻精度要求达到 5.7nm,这无疑对光刻机运动台的位置测量提出了更高的精度要求。

图1 测量光栅和读数头相对位置Fig.1 Relative position of measuring grating and reading head
目前,应用于光刻机运动台定位的超精度、高分辨率和大行程位移测量传感器主要是激光干涉仪和光栅位移传感器。激光干涉仪以激光波长作为测量基准,受环境因素影响较大。光栅位移传感器以光栅的栅距作为测量基准,与激光干涉仪相比,受环境因素影响相对较小,在成本和环境控制方面具有很大优势[2]。针对28nm浸没式光刻机以及14nm预研对位置测量提出的超高精度要求,环境误差对于光栅尺位移测量系统的影响已经不可忽略。热误差作为影响光栅尺位移测量系统测量精度最主要的环境误差项,它的存在大大地增加了测量结果的不确定度。
本文依托桂林电子科技大学承担的国家02专项子课题《高精度位置测量系统在线标定技术研究》,设计并搭建了具有纳米级分辨率的光栅尺位移测量系统。为了能够得到环境温度变化对测量系统的影响,应用COMSOL有限元分析软件对测量光栅和读数头进行了热-结构耦合分析,得到了光栅和读数头镜组的热态特性,为实际应用中光栅尺位移测量系统的环境控制提供了参考,也为下一步通过实验方式检测环境误差对测量系统的影响奠定了基础。
1 COMSOL建模和边界条件计算
1.1 光栅尺、读数头镜组有限元模型建立
如图1所示,为测量光栅和读数头的相对位置分布图,4块规格为68mm×68mm×9mm的一维光栅逆时针依次旋转90°布局于光栅承载台上,4个读数头由读数头安装基板固定在测量光栅的Z轴正向,同4块光栅一样呈交叉分布形态对应部署于每块测量光栅上方。测量光栅和读数头镜组作为测量系统重要的组成部分,对于测量环境温度变化比较敏感,下面将利用COMSOL有限元分析软件来建立它们的有限元模型,以便进一步分析环境温度变化对它们的影响,如图2所示为测量光栅和读数头镜组的有限元模型图。
1.2 热源
1.2.1 直流电机发热
一般地,直流电机的热消耗功率计算公式为[3]:

式(1)中,R=R20[1+α(TN-20℃)]为相电阻,单位为Ω,其中,α为温度系数;I=F/KF为有效电流,其中,F为电机动力,单位为N,KF为常量,T=20℃时,KF=116。
通过阅读PI微型定位六足运动台的技术文档可知:分别安装于运动台六足上精密冷却器可排出电机所产热量的95%~99%,只有很小一部分热量会传递到六足运动台上表面。
测量光栅和读数头未与运动台直接接触,所以在热分析时,将电机工作产生的热量转化为对应的环境温度载荷施加于测量光栅和读数头外表面。
1.2.2 激光电磁热
测量系统采用的激光器能够输出功率为900mw、光斑直径6mm的激光束,入射激光束通过读数头的入射光轴射入到内部光学元件的表面,一部分能量在通过光学元件表面时被反射掉,另一部分则被光学元件吸收使得光学元件温度升高,从而在测量空间中形成一个局部热源,并按照固体热传导规律在光学元件内部或各光学元件之间进行能量传递。由于热量的传递会在光学元件中形成不同的温度分布,该温度场分布主要取决于光学元件表面的吸收系数、用于制造光学元件的材料的热传导系数、比热容以及激光功率密度等。由激光产生的热量在光学元件中的扩散状态可用函数表示为:

式(2)中,ρ(T)为光学材料的密度;c(T)为光学材料的比热容;T为温度;k(T)为光学材料的热传导系数;q(r,t)v为单位体积的热产生率。读数头内部光学元件的材料属性见表1。

表1 光学元件材料属性Table 1 Optical material material properties
考虑到光学元件的温度场变化,是外部结构件热传递和激光辐射加热共同导致的结果。故在三维坐标系下的传热方程可表示为[4]:

1.3 初始条件和边界条件
1.3.1 初始条件
假设环境温度为20℃,测量光栅和读数头镜组的初始温度也为20℃。
1.3.2 自然对流传热
由努谢尔特准则可知,自然对流的换热系数计算公式为[5]:

式(4)中,Nu为努谢尔特数;λ为流体导热系数,单位为W/(m·℃);D为特征尺寸,单位为m。由此式可知,努谢尔特数是计算换热系数的关键,可通过下面得表达式求得[6]。
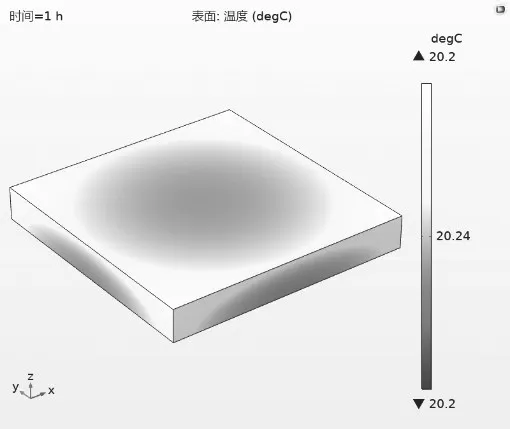
图3 测量光栅温度分布图Fig.3 Temperature distribution of measuring grating
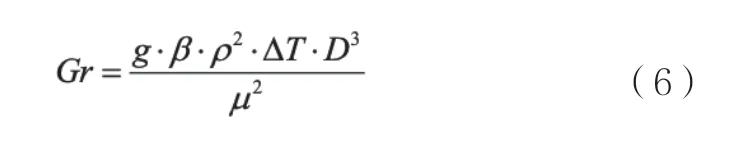
式(5)和式(6)中C、n为常数,可通过查表得到,定性温度取壁面温度与流体温度的平均值;Ra为瑞利数;Gr为格拉晓夫数;Pr为普朗特数;g为重力加速度,单位为m/s2;β为流体的体积膨胀系数,单位为℃-1;ρ为流体的密度,单位为kg/m3;ΔT为换热表面与流体的温差,单位为℃;μ为流体粘度,由流体固有物理性质决定的物理量,单位为pa·s,即N·s/m2。对于测量光栅和读数头来讲,都属于自然对流方式传热,计算得到的光栅尺上表面的换热系数为1.2W/(m2·℃),侧立面的换热系数为0.4W/(m2·℃);读数头下表面的换热系数为1.3W/(m2·℃),侧立面的换热系数为0.8W/(m2·℃)。
2 光栅尺和读数头镜组热特性研究
2.1 光栅尺热变形仿真及结果分析
通过前面边界条件的计算,在COMSOL中对光栅尺材料属性和边界条件进行设定。由于光栅是通过光栅承载台固定于六足运动台上表面,光栅在Z轴负向的位移量为0,故在固体力学仿真中将光栅的下表面设置为辊支撑,余下光栅外表面与空气之间通过自然对流方式进行传热。运动台工作1h,测量光栅附近温度升高1℃,将该温度作为光栅仿真的载荷,得到如图3所示的光栅温度分布图。
测量光栅基底采用低膨胀系数的微晶玻璃,如图3所示,运动台工作1h,测量光栅周围环境温度提高1℃的条件下,测量光栅的自身温度提高0.2℃,呈现出较为均匀的20.2℃。此时光栅的形变量如图4所示,达到稳态时的光栅形变量如图5所示。
从仿真结果可以看出,当环境温度升高1℃时,测量光栅沿X、Y和Z方向上都会发生形变,1h的最大形变量为0.12nm,达到稳态后的最大形变量可达到0.49nm,而光栅中间位置的形变量则很小。因此,光栅形变不仅与温度相关,与在测量光栅中的位置分布也关系密切。当测量光栅四周的形变量达到0.5nm时,也就意味着测量光栅的行程要增加近乎1nm,这是光刻机运动台的超高精度要求是不允许的。

图4 工作1小时光栅形变量Fig.4 Grating deformation for 1 hour of operation
为了更加直观地描述光栅热变形对测量结果的影响,下面以X方向为例,分析单个光栅热变形带来的零位漂移误差和示值误差。如图6所示为X方向光栅热变形前后的示意图,图中OX和OX'分别为光栅热变形前后X方向光栅的零位;L和L'分别为光栅热变形前后光栅总长度;X和X'分别为光栅热变形前后光栅上任意一点到零位的距离;L1和L1'分别为光栅热变形前后光栅中点到光栅零位的距离;L2和L2'分别为光栅热变形前后光栅中点到光栅末端的距离;P和P'为X方向光栅中点,由光栅的形变图可以看出光栅中间位置形变量很小,因此可近似认为P和P'为同一点。
从图6中可以看出:

光栅热变形会导致光栅长度发生变化,则可得到光栅热变形后的光栅零位位置为:

则光栅在X方向上的零位漂移误差δ0,其表达式为:

通过阅读PI运动台的技术文档可知,运动台在X正方向上的最大位移量为16mm,位于区间[0,L1]内,则光栅上任意一点的位置在光栅热变形前后的关系可表示为:
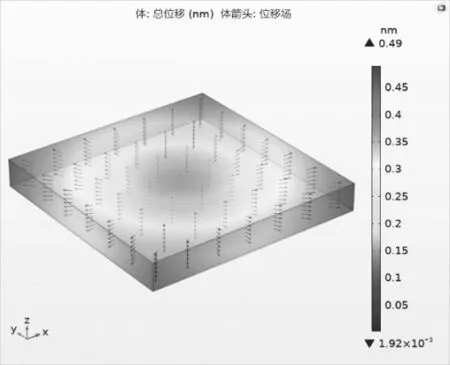
图5 稳态后光栅的形变量Fig.5 Deformation of the grating after steady state
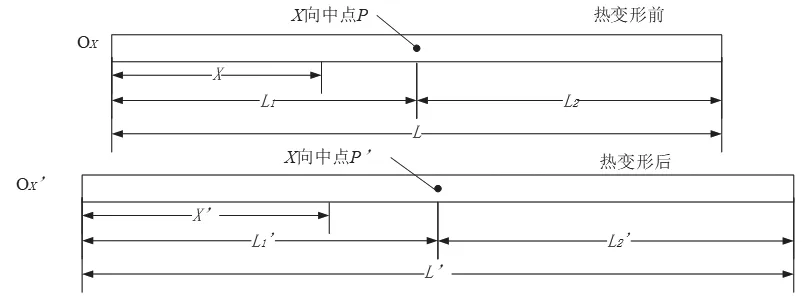
图6 X方向光栅热变形前后示意图Fig.6 Schematic diagram of the X-direction grating before and after thermal deformation
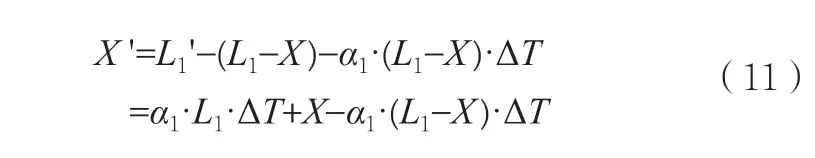
由此可得到示值误差δ1为:
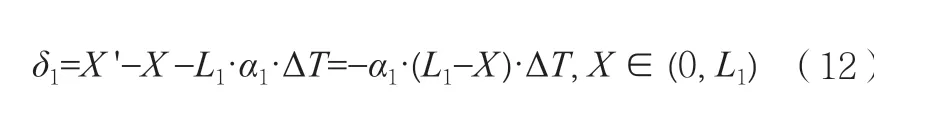
结合前面的仿真结果可得到,当测量光栅周围温度升高1℃,光栅在X方向上的零位漂移误差和示值误差最大可达到-0.49nm,大大地增加了测量结果的不确定度。
2.2 读数头镜组热变形仿真及结果分析
读数头镜组的温度载荷由外部环境温度和激光电磁热共同导致,在初始状态下读数头镜组和外部结构件的温度都为环境温度20℃。

图7 读数头镜组温度分布Fig.7 Temperature distribution of the reading head lens group
如图7所示,初始时刻读数头镜组的温度与外界温度相同,工作1h后,在外部环境温度上升1℃的情况下,读数头镜组的温度分布也随之发生变化,与外部结构件接触面最多的偏振分光镜温度最高,角锥棱镜温度相对较低,由于仿真中光学元件都采用同种材料,导热系数相同,所以不同光学元件间的温差不大。
图8为外界环境温度升高1℃时读数头的形变量,最大形变值为0.09μm,平均热漂移系数约为0.05μm/℃。为了进一步分析环境温度变化对读数头的影响,下面将结合仿真得到的结果分析由于温度变化导致的读数头折射率变化。由前面的读数头温度分布图可知,当测量环境温度升高时,读数头镜组温度呈现出明显的梯度分布。读数头镜组所用光学材料的折射率会随着温度变化而变化,此时的读数头镜组就相当于一个梯度折射率镜组,折射率的分布与镜组中的温度梯度有关,可结合对应的折射率温度系数求得。
通常情况下,一定温度范围内的折射率温度系数被认为是一个常数,即折射率和温度为线性关系,线性化系数为折射率温度系数,记为dn/dt,故读数头镜组的折射率分布表示为:

式(13)中,n0为读数头镜组表面一点处的折射率;Δt为读数头镜组内部的温差;d0为镜组厚度。上式是没有考虑读数头镜组形变时折射率的分布,而镜组上某点的实际折射率是按照真实位置的折射率来计算的,即需要考虑镜组形变的影响,故需对式(13)进行修正,使用镜组形变后的厚度d '来代替原始厚度d0。
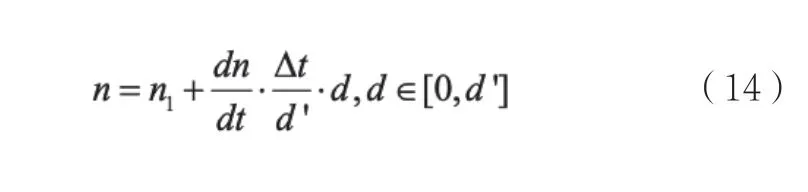
由于读数头镜组表面一点处的温度不一定是读数头镜组所使用光学材料折射率对应的标准温度,因此n1不能直
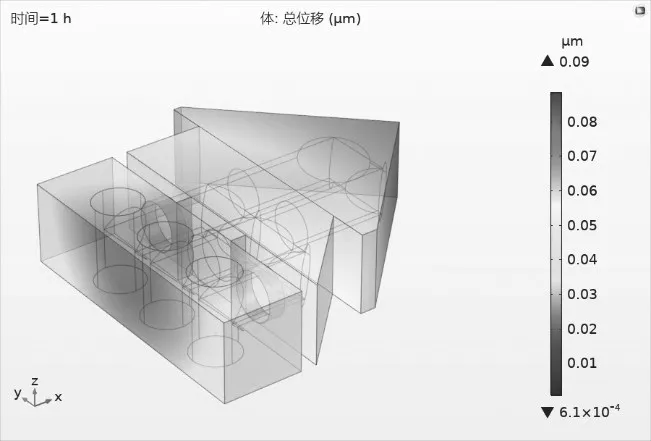
图8 读数头镜组热漂移Fig.8 Reading headlens group thermal drift
接用标准温度下的折射率来计算,其计算公式为:
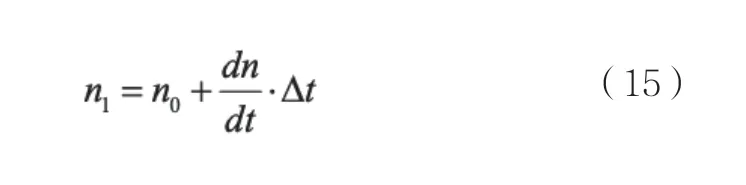
式(15)中,n0为标准温度下光学材料折射率;Δt为实际温度于标准温度存在的温度差。
3 结束语
上述的有限元仿真结果表明:光栅尺位移测量系统工作1h,测量光栅附近温度升高1℃的情况下,达到稳态的光栅最大形变值为0.49nm,由此带来的光栅在X方向上的零位漂移误差和示值误差最大可达到-0.49nm;读数头镜组最大形变值为0.09μm,平均热漂移系数为0.05μm/℃,镜组温度和折射率呈现出明显的梯度分布。为了进一步获得实际工况下由环境温度变化带来的测量误差,下一步将通过实验方式来检测环境温度变化对测量结果的影响。
