因惑施教

屈婷 袁凌云

面积是对一个平面（物体或图形）表面多少的测量，其本质是某个单位量的数值化表示。这个“单位量”是什么样的？面积与周长有什么本质区别？什么时候要求周长，什么时候又该求面积？这些都是学生认识面积概念时的难点。如何因“惑”施教，实现对面积的真正理解？

一、动作表征，建立表象

在教学中，教师可以先引导学生了解周长与面积的动作表征是有本质区别的。

师（多媒体出示两个面积差距较大的正方形及两种不同型号的排笔）：如果要给这两个图形涂色，你准备选择哪支笔？

生1：选大号的排笔，涂得快。

生2：大的要用大排笔，小的要用小排笔，因为小的也选大排笔，容易“涂过”。

师：你说的“大小”是指什么？

生2：“大小”是指它们的面积。

师：“涂过”是什么意思？

生2：就像我们用水彩笔涂色一样，超过小正方形的四条边，就会涂过。

师：看来面积也是有边界的。摸一摸，哪里是它们的面积？（大部分学生用整个手掌来摸大正方形的面积，用一根指头来摸小正方形的面积）为什么不用手指摸大正方形？

生3：手指头太小了，需要摸很多次。手掌大一些，摸一次就够了。

师：长方形和正方形都是平面图形，其他平面图形有面积吗？

生4：三角形、圆形、平行四边形、梯形等都有面积。

生5：线段、角没有面积。

学生在摸的过程中，不仅将面积的动作表征和表象建立起联系，而且意识到排笔刷、手掌、手指都是描述面积的间接单位，从而积累了以面量面的经验。

二、细分图形，触摸本质

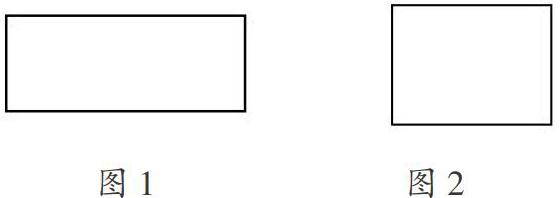
教师课前为学生准备了如下材料：剪刀，长5厘米、宽2厘米和长4厘米、宽3厘米的长方形实物卡片，画在练习纸上的与实物卡片一样大的长方形（图1、图2）。

师：上面这两个长方形，哪个面积大？

生1：看不出来。

生2：图1又细又长，图2又短又宽，用重叠的方法也比较不出来。

师：重叠一次不能比出谁大谁小，这可怎么办？

生3：多重叠几次。

学生操作之后，有两种典型方法：一是将图1和图2多次重叠，依次剪掉重叠部分，比出大小;二是利用两种不同材料的重叠（如长5厘米、宽2厘米的卡片和练习纸上长4厘米、宽3厘米的长方形重叠产生区域A）在练习纸的两个长方形内部进行分割，细分为不同的小长方形，再比出大小（如下图）。

师：这样重叠后，能比较出面积的大小了吗？

生1：图2面积大一些。

师：你更欣赏哪种剪法？

生2：方法1把长方形剪开了，但是要想让别人看清楚，还要把零碎的图形拼起来。

生3：剪开再复原太麻烦，很容易弄错。

生4：方法2没有剪开，看得更清楚。

师：图2比图1大多少？

生5（指着区域C比画）：大这么多。

师：如果用它作单位，图1可以分割成多少个这样的小长方形？老师为每个同学都准备了一个这样的小长方形，咱们用它作单位来分分看。

师（展示学生的作品）：有了单位，我们就可以数了。现在可以怎样描述图1长方形的大小？

生6：图1里有5个这样的小长方形。

师：有一个同学是下图这样分的，你有什么想法？

生7：有个小长方形画“分家”了。

师：是呀，分割时，要保证每个图形大小完全一样。

生8：正方形也可以作为标准来数出长方形的大小。

师：你能具体说说吗？

生8：把每个小长方形都一分为二，这样长方形1里就有10个小正方形。

师：你的想法真是太巧妙了。平面图形那么多，还有哪些平面图形可以作为标准？

生9：所有的平面图形都可以。

生10：线段不行，角也不行。

师：为什么？

生10：线段只能量长度，铺再多也铺不满;角不封口，也不行。

师：选择一个标准铺一铺，想一想：哪个平面图形作面积单位最合适？

數学上对面的研究，不仅关注它的形状，还关注它的大小，即面积。在用不同平面图形密铺长方形的过程中，学生体会到：测量物体的面积要尽可能“量尽”，等腰三角形、圆形无法铺满，等边三角形和长方形都可以转化为正方形，正方形长和宽相等，二维度量单位统一，不需考虑摆放问题，优越性显而易见。

三、链接生活，深化感知

教师出示以下题目。说一说：下面所需材料是指图形的周长还是面积？（1）在钉子板上围四边形;（2）用卡纸做长方形卡片;（3）用铁丝做正方形;（4）用铁皮做正方形;（5）粉刷正方形墙壁;（6）给长方形地铺地板;（7）给长方形板报贴花边。

学生遇到单纯的求图形的周长和面积问题时，一般不会把“线”“面”混淆，但一涉及解决生活中周长与面积的实际问题时就理不清思路。因此，笔者设计了思考所求问题到底与周长有关、还是与面积有关的练习，让学生将制作图形所需原材料的特点与周长或面积进行匹配，将学生对“面积”的生活经验转化为数学经验。

经历上面的练习题后，教师还可以将习题变一变：提供软铁丝做的长方形框架、长方形纸片两种材料。①要改变图形的面积，你准备选择哪种材料进行操作？学生充分操作后，引导学生发现：不管怎样裁剪，只要纸片没有遗失，面积之和就不会发生变化。②为什么软铁丝做成的图形的面积会发生变化？学生通过操作又得出软铁丝可以做成不同的形状，形状不同，面积也不相等的结论。③软铁丝并没有变长也没有变短，为什么围成的图形面积发生了变化？学生又发现软铁丝是图形的周长，这个材料不管做成什么形状，原材料没有变化，周长就不会发生变化。④谁能用软铁丝做成面积更小的形状？学生得到铁丝尽量往里缩，面积就越小，尽量往外放，面积就越大的结论。

图形的周长与面积虽没有本质联系，但某个因素一变化，就会有无数种可能。长方形纸片的面积看得见、摸得着，学生认为便于操作，要改变面积极其容易。可是长方形纸片的面积一旦固定好了，无论剪掉哪一块，再填补到其他地方，面积之和都没有增加或减少。软铁丝做的框架，看似摸不着面积，但这样的软铁丝可以因物赋形，它围成的面积大小取决于围成的形状。

（作者单位：宜城市窑湾小学）

责任编辑  张敏