开架式水下机器人操纵性水动力系数计算
2020-05-03薛乃耀王冬姣叶家玮刘鲲
薛乃耀 王冬姣 叶家玮 刘鲲


摘 要:开架式水下机器人结构复杂,其操纵性水动力学模型具有高度非线性且是耦合的,航行性能也因结构多样而不相同。为完成清污水下机器人的推进器布置方案,基于零航速展开的二阶水动力模型,采用Fluent数值仿真方法模拟机器人的直航、斜航和定轴回转运动,并通过AQWA获得水下机器人的附加质量矩阵。根据获得的水动力情况配置ROV推进系统,通过最小二乘法拟合获得清污水下机器人的各项水动力系数。
关键词:水下机器人;水动力模型;数值计算
中图分类号:U661.1 文献标识码:A
Abstract: The structure of the open-frame underwater remote operated vehicle (ROV) is complex, its maneuverability hydrodynamic model is highly nonlinear and coupled. and the navigation performance of the ROV varies with structures, therefore it is difficult to build a maneuverability model with enough accuracy. In order to complete the layout of the propeller system of the ROV, based on the second-order hydrodynamic model expanding at zero speed, Fluent numerical simulation method is adopted to simulate the direct navigation, oblique navigation and fixed-axis rotary motion of the ROV, and the added mass matrix is obtained by using AQWA. According to the result of the numerical calculation, the thruster system is built and the hydrodynamic coefficients are computed according to least-square method.
Key words: Underwater robot; Hydrodynamic model; Numerical calculation
1 引言
遙控带缆水下机器人(ROV)在海洋资源开采、海洋探测和海洋工程作业中应用广泛。目前ROV多为开架式结构,机箱、浮体、螺旋桨以及作业工具直接安装于机器人框架上,结构复杂。水下机器人的操纵性是其水下作业能力的重要影响因素,其主要受机器人的结构、推进系统配置和控制律影响。要使水下机器人的作业能力满足设计要求,必须综合考虑机器人的水动力性能,为推进系统的选择提供依据。2015年,挪威科技大学Ole Alexander Eidsvik[1]利用基于势流理论的CFD软件WADAM计算了多种型号水下机器人的附加质量,并与经验公式、实验数值及WAMIT计算结果作对比,若实验仪器精度不足,则CFD计算结果与参考值更为接近。
自主式水下机器人和载人潜水器的水动力模型大多为潜艇运动方程,基于一个定常运动速度和小扰动叠加得到。通过以定常运动为基准点进行泰勒展开,导出潜艇运动的水动力系数。对于本文设计的水下清污机器人而言,由于液压系统和作业工具的存在,三向不对称,作业期间推进系统的主要任务为定点悬停和姿态调整,基于定常运动的潜艇水动力模型并不适用。本文采用文献[2]的开架式ROV水动力模型,通过ANSYS-AQWA和Fluent计算水下机器人的水动力系数,为其推进器配置选型以及结构优化提供依据。
2 水动力函数
作业型ROV为满足作业要求,通常需要进行较为灵活的操纵,因而设计航速较低,纵向直航不是ROV的主要运动。徐诗婧[2]参考Fossen等[3]学者的研究结果,将ROV水动力模型表示为速度和加速度的函数,并以零航速为基准点展开至二阶。考虑到ROV存在结构不对称性,在不对称方向的运动所产生的水动力受到运动方向的影响,在二阶展开式的基础上加入部分系数作为补充。
3 计算工况
3.1 惯性类水动力
ROV的惯性类水动力通常通过平面运动机构试验获取,在六自由度方向分别进行纵荡、横荡、垂荡、横摇、纵摇和首摇试验。这种方法需要进行多次重复试验或者数值仿真计算,并需要改变运动频率以获得更为准确的计算数据。这对于水下机器人的初步设计而言并不有利,而Ole Alexander Eidsvik[1]的对比结果表明,基于势流理论计算附加质量具有一定的可靠性。本文水下机器人的附加质量矩阵通过ANSYS AQWA经一次计算获得,并按照SNAME(1950)[4]对海洋航行器运动规范定义速度、作用力等符号。
对于水面航行船舶,其附加质量与波浪频率相关;而水下航行器当航行深度足够大时,其水动力系数与波浪激励频率无关[3]。在AQWA中计算附加质量时,将ROV航行深度设置为水面以下20 m,质量、惯性矩等参数采用Solidworks建模数据,具体参数如表2所示(坐标原点位于ROV框架中心)。
3.2 粘性类水动力
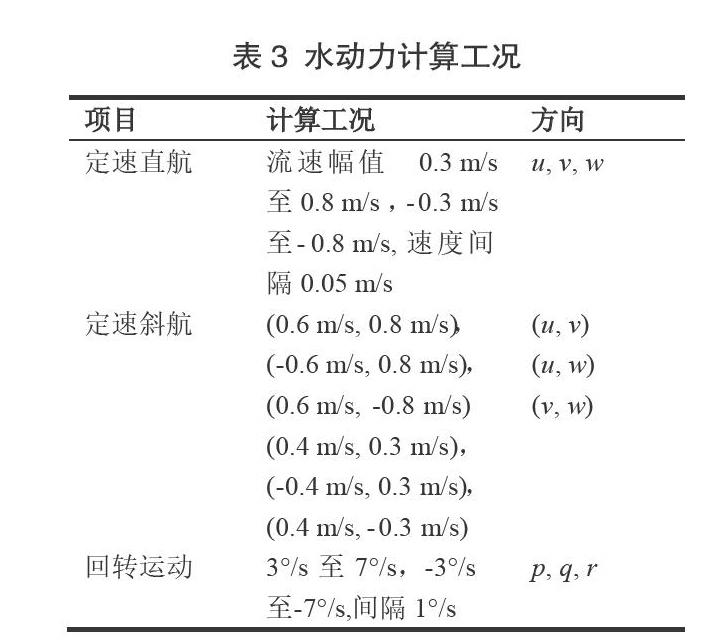
ROV的粘性类水动力系数通过Fluent数值计算获取。其中与线速度相关的粘性类水动力可以通过直航和斜航数值模拟计算获得,计算工况如表3所示。在三向不对称情况下,各个速度方向的变化均会对ROV水动力产生影响,在斜航数值模拟中,通过在速度入口直接设置速度分量的方式模拟ROV的斜航运动,斜航运动数值实验分组以速度(Vi, Vj)表示。使用这种方法,可以避免斜航运动中漂角和攻角变化后需要重新划分网格的问题,并减少了数据输入和结果处理的计算量。
在ROV的姿态调整工况中,ROV通常进行定轴转动。许孟孟[5]分别采用运动参考坐标系方法(MRF)和重叠网格方法进行潜水器的定点转首工况的计算,获得了复杂外形潜水器的回转水动力,并将计算结果代入Simulink模型中进行回转控制模拟,其结果与实验结果相近。因此,在估算ROV旋转水动力系数时采用MRF方法,计算工况如表3所示,忽略回转运动的耦合水动力的影响。
4 计算結果
在AQWA中划分网格,如图1所示。网格数为23691,设置计算频率10个(由程序指)定。通过查询计算结果可知,每个频率所得到的附加质量矩阵相同,与无界流中附加质量与频率无关结论一致。
对水下机器人进行粘性水动力计算前,先进行网格无关性检验。网格无关性检验取航速0.8 m/s直航运动作为算例,分别以170万、270万、369万及650万网格进行计算。计算结果如图2所示。最终采用网格数369万的计算方案,对ROV的直航和斜航运动进行数值模拟,计算时ROV固定,通过设置入口来流速度改变ROV航速。因为ROV声呐信标安装位置为ROV框架中心,作用力和力矩的输出基准也设置为ROV框架中心,基准轴方向平行于全局坐标系。
(1)直航工况的计算结果,如图4所示。在x方向上的不对称性引起的阻力变化较小,由于机器人存在抱抓,x方向投影面积较大,并产生了极大的z轴力矩,航速为0.8 m/s时达到了229 N·m;此外,ROV框架内部设备较多布置于yz平面上且直接外露于流场中,水流在流经x方向时产生的航行阻力远大于其余方向;z轴受两侧浮力材料遮挡的影响,ROV框架内设备布置不对称对沿z方向直航阻力影响不大,但是抱臂和机械臂的存在使ROV在沿z方向直航时伴有较大的回转力矩,航行稳定性极差;在y方向,ROV存在明显的不对称性,在正方向和负方向航行时阻力幅值具有明显的差异,但是这一方向上的直航阻力仅稍大于z方向阻力,且在其余自由度上产生的阻力和力矩幅值极小。
(2)斜航工况的计算结果,如表4所示。x, y, z分别表示来流方向,Fluent中输出在固定坐标系下的作用力,Fx、Fy、Fz分别表示固定坐标系下的水动力,Mx、My、Mz分别表示固定坐标系下的力矩。
(3)回转水动力仅在回转方向有较为显著的作用力,因此忽略回转运动方向以外的水动力影响,其计算结果如图5所示。
根据以上水动力计算的结果,可以考虑ROV的推进器布置方案并将ROV的首向选择为y方向。
从首向控制而言 ,x方向和y方向需要的控制力矩相当,但x方向阻力过大,航行稳定性较差。若将ROV的主推进器沿x轴方向布置,则航行时推进器需要频繁调整推力输出,以保证ROV保持直航,这对推进系统而言负荷过大。由于浮体的存在,z方向虽然航行阻力较小,但是难以布置推进器。因此,在配置ROV的推进螺旋桨时,将三个主推进器设置于ROV底部,推力沿y方向。两侧浮体各有一个沿x方向的螺旋桨,辅助ROV航行时的姿态调整,此时图3中y, z, x方向分别为ROV的纵荡、横荡、垂荡方向。
最终,对水动力系数拟合按照此坐标系计算,得到:纵荡方向直航运动、横荡方向直航运动、垂荡方向直航运动、纵荡-横荡耦合、纵荡-垂荡耦合、纵荡-横荡耦合水动力系数。其中较为显著的部分系数及附加质量如表5所示。
5 总结与展望
通过综合利用ANSYS AQWA和Fluent,快速获取开架式清污水下机器人的航行阻力和水动力系数,并根据数值计算得到的ROV水动力性能,综合考虑阻力和ROV框架的剩余空间,配置推进螺旋桨布局。以零航速为基准点,采用最小二乘法拟合得到ROV的水动力导数。
在后续的研究中,将以本文求得的水动力系数为基础,设计清污水下机器人的自适应运动控制算法,进行实验验证并更新机器人的水动力系数,以获得更为准确的水动力计算模型,提高水下机器人航行控制和作业精度。
参考文献
[1] EidsvikO A . Identification of Hydrodynamic Parameters for RemotelyOperated Vehicles[J]. 2015.
[2] 徐诗婧. 开架式ROV水动力特性与运动仿真研究[D].哈尔滨工程大学,2018.
[3] Fossen T I. Handbook of Marine Craft Hydrodynamics and Motion Control[J]. IEEE Control Systems, 2016, 36(1):78-79.
[4] SNAME (1950). The Society of Naval Architects and Marine Engineers. Nomenclature for Treating theMotion of a Submerged Body Through a Fluid. In: Technical and Research Bulletin No. 1–5.
[5] 许孟孟, 冯正平, 毕安元, 樊斌, 姜涛. 复杂外形潜水器旋转水动力的计算[J]. 上海交通大学学报,2018,52(07):764-769.
