面向“货到人”拣选系统的一种随机调度策略

李 腾，冯 珊

(哈尔滨商业大学 管理学院，黑龙江 哈尔滨150028)

电商的迅速发展为物流带来了新的挑战，传统的“人到货”拣选系统中，拣货员的拣货时间占其工作时间的60%～70%，这种拣选方式效率较低，已经不能满足消费者对配送时间的需求[1]。随着美国亚马逊Kiva系统的广泛应用[2]，在拣选系统中采用AGV配合人来完成拣选作业受到了越来越多的关注。这种“货到人”的拣选方式可以大幅度提高拣选效率，具有更好的灵活性[3-5]。对于该拣选系统，如何进行AGV调度是影响拣选系统效率的主要因素。

近年来，许多学者从不同角度对AGV调度问题进行了研究。傅正堂等[6]研究了AGV调度问题，从AGV初始剩余电量不同的角度，考虑AGV空载与重载耗电量的差异，建立AGV调度模型，解决初始电量不同的AGV调度问题，减少AGV使用数量，并提高了作业效率。梁承姬等[7]考虑中转平台与容量约束，以任务完成时间最短为优化目标，建立具有时间窗约束的AGV调度模型，利用遗传算法求解模型，解决AGV的调度问题，减少了作业时间。韩晓龙等[8]设计3种不同的AGV调度策略，通过仿真分析，得出AGV调度与数量配置是提高效率的关键因素，最后对AGV调度策略与数量配置提出了建议。Fazlollahtabar等[9]对AGV调度进行研究，考虑AGV提前到达会造成等待时间的浪费，以最小化提前到达与迟到的惩罚为目标函数，实现了AGV的调度。Singh等[10]针对AGV调度问题，提出一种新的调度方案，将车间加工区域进行划分并为每个区域分配一台AGV，提升了系统运行的效率。沈博闻等[11]针对AGV调度问题展开研究，考虑系统的拥塞程度，通过对AGV完成任务的总代价进行优化，实现了AGV的智能调度并降低了系统的运行成本。袁瑞萍等[12]针对AGV调度问题，提出多个拣选台同步拣选与异步拣选2种拣选方式，以所有任务的完成时间最短为优化目标，建立2种拣选方式下的AGV调度模型，利用改进遗传算法对两调度模型进行求解，通过实例仿真得出同步拣选具有更高的效率，同时解决了AGV的调度问题。

目前，多数学者针对不同领域的AGV调度问题进行研究，上述文献中任务的下发方式为一次下发。而在实际工作过程中，任务通常是以分批的形式下发，并且多数文献只考虑了AGV的运行时间，没有考虑到AGV的排队等待时间。大多数系统在进行AGV调度时，通常会调度空闲的AGV来完成当前的任务以减少任务的完成时间，但这也会导致AGV的等待时间增加，使任务的完成时间增加。因此，本文针对“货到人”拣选系统，提出分批下发任务情况的一种随机调度策略，同时考虑AGV在拣选台的排队等待时间，以所有任务的完成时间最短为优化目标，进行AGV随机调度。

1问题描述

“货到人”拣选系统的布局如图1所示，货架之间的区域为AGV的行走通道，拣选区域由多个拣选台组成，每个拣选台有1名拣选人员完成拣选作业，多个拣选台可以同时作业，系统中的AGV可以在不同的拣选台等待拣选。系统接收客户订单后，仓库管理系统将某一时间段内的订单按照其任务是否在同一货架上的规则进行分批处理，然后将处理后的任务发送至调度系统，调度系统进行AGV的调度并将任务进行分配。此时，AGV将从初始位置到达被分配任务所在的货架位置识别货架，将其搬运至指定的拣选台等待拣选。拣选人员确定货物信息后，在该货架的指定货位将所需货物拣出并进行扫描。扫描完成后，拣选人员将货物放至指定的货筐中，同时AGV将此货架搬运至原来的位置，并在该位置等待任务的再次分配。在AGV完成任务的过程中，如果电量低于安全电量，AGV将在完成当前任务后，到达充电区进行充电，直到充满才可以对其分配任务。

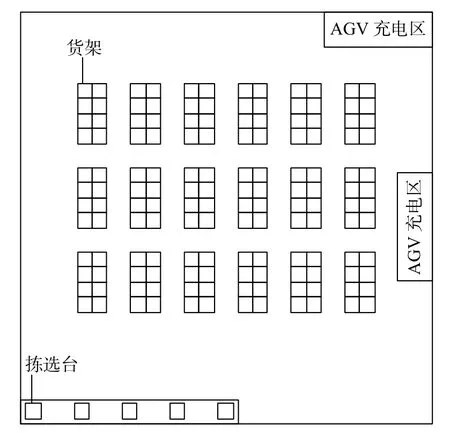
图1“货到人”拣选系统布局Figure 1 Layout of the "rack to picker"picking system

本文所提随机调度策略是指将任务进行分配之前，不确定AGV的状态，任务可以分配给所有的AGV来完成。如果在任务分配的同时，AGV处于忙碌状态，则需要等待该AGV完成上一个任务后才能完成该任务。这种调度策略下部分目标货架可能需要等待，会造成时间的浪费，但相比于目前使用较多的调度空闲AGV策略可能会得到全局近似最优解。调度空闲AGV策略是指确定系统中AGV的状态，任务每次只分配给空闲的AGV来完成。这种调度策略虽然解决了目标货架的等待时间的浪费，但不能从全局的角度进行AGV的任务分配。本文通过优化AGV完成所有任务所用时间来提高拣选效率。

2模型构建

2.1研究假设

针对“货到人”拣选系统调度策略，本文做出如下假设。

1)初始时刻，系统中的所有AGV处于空闲状态；

2)完成任务的过程中，系统中所有AGV的电量始终大于安全电量；

3)AGV将货架搬回后，在该货架位置等待下一次任务的分配；

4)AGV在完成任务的过程中，始终匀速行驶，并且所有AGV的行驶速度相同；

5)AGV在行走过程中，不存在避障等状况；

6)货物是随机存储在货架上的；

7)每个拣选台对应的拣选人员每次完成拣货工作的时间相同，分货时间相同。

2.2参数设计

1)m为AGV的总数量，n为任务的总数量，q为 拣选台的总数量；

2)i为第i台AGV，i∈[1,m]，j为第j个任 务，为第k个拣选台

3)(xAi,yAi)表示第i台AGV的位置坐标，表示第j个任务的位置坐标， (xPk,yPk)表示第k个拣选台的位置坐标；

4)d1io j表 示第i台AGV从初始位置到第j个任务所行驶的最小距离，d2i jk表示第i台AGV从第j个任务到第k个拣选台所行驶的最小距离，d3ik j表示第i台AGV从第k个拣选台回到第j个任务所行驶的最小距离。本文所有最小距离计算均采用曼哈顿距离，即

5)v表示AGV的行驶速度；

6)t1表 示拣选人员的拣货时间，t2表示拣选人员的分货时间；

7)r表示每个拣选台一次呼叫任务的数量，每次呼叫的时间点为上一批任务中最早到达该拣选台的时间点，其中r∈[1,n]；

8)l表示任务到达拣选台的顺序，序号l∈[1,n]；

9)tcj表 示第j个任务被呼叫的时间点；

10)tlk j表 示第l个 到达第k个拣选台的第j个任务到达该拣选台的时间点；

11)tp(l-1)k j表 示第l-1个 到达第k个拣选台的第j个任务被拣选完成的时间点；

12)tbi j表示由第i台AGV完成的第j个任务被拣选完成后，该AGV回到该任务位置的时间点；

13)tqilk j为由第i台AGV完成的第l个 到达第k个拣选台的第j个任务在该拣选台的等待时间tqilk j=

14)T i为 第i台AGV完成被分配任务所花费的总时间；

[38]王裕巽估算，嘉靖一朝四十五年，白银采纳总额共计1928100两。王裕巽：《明代白银国内开采与国外流入数额试考》，《中国钱币》，1998年第3期。

15)T为所有任务的完成时间；

16)决策变量Xi j表示第i台AGV是否完成第j个任务，且

2.3随机调度策略模型

在拣选系统中，一批任务的完成时间为所有AGV完成各自被分配的任务所花费的最长时间。本文以耗时最长的AGV的完成任务时间最短为目标函数，最小化订单的完成时间，以任务分配为决策变量，考虑AGV在拣选台的排队等待时间，建立随机调度策略模型。

上述模型中，Xi j为决策变量；式(1)为最小化所有AGV中完成各自任务的最长时间；式(2)将其分为AGV完成任务所行走的时间与AGV在拣选台的排队等待时间，其中，AGV的行走距离分为3个部分，d1io j为该AGV上次完成的任务所在位置；式(3)为由第i台AGV完成的第l个 到达第k个拣选台的第j个任务在拣选台的排队等待时间，与该AGV所在排队队列中的前一台AGV被拣选完成的时间点和该AGV到拣选台的时间点有关；式(4)为任务被拣选完成的时间，由AGV到达拣选台的时间点、AGV的等待时间、拣选人员的拣货时间以及分货时间决定；式(5)为AGV将货架搬运至原来位置的时间点；式(7)表示系统中的每个任务只能由一台AGV完成。

3模型求解

遗传算法在求解组合优化问题时，具有操作简单、并行性、计算效率高、通用性以及稳定性等特点[13-14]。由于AGV调度问题与任务分配问题属于组合优化问题，并且采用遗传算法中实数编码的方式可以将AGV的调度结果、任务分配结果以及拣选序列直观地体现出来，因此，本文采用遗传算法对上述模型进行求解。

1)生成初始种群。首先确定初始种群的数量与每次呼叫任务的数量。然后，将订单中所有任务进行分组，每组任务中不能调度相同的AGV。最后，采用实数进行编码生成染色体，如图2所示。染色体的长度为单个订单中任务的总数；每个基因位代表一个任务；基因位上对应的值表示该序号的AGV完成该位置的任务。这种编码方式可以缩短染色体的长度，直接观察出每台AGV完成的任务以及同一台AGV完成任务的先后顺序。

图2染色体编码方式Figure 2 Chromosome coding

2)计算适应度值。每条染色体的适应度值为所有AGV完成各自全部任务耗费时间中的最大值的倒数。适应度函数为

3)选择。选择一定数量的适应度值较高的优良个体作为父代。

4)交叉。按照交叉概率，采用不定点交叉的方式进行交叉操作，过程如图3所示。将染色体按照每次呼叫任务的数量进行分段，在任务的组数范围内随机生成2个值为交叉位置，表示一条染色体的某段基因与另一条染色体的某段基因进行交叉。

5)变异。按照变异对染色体进行变异操作。在任务总数范围内，随机产生一个整数表示发生变异的基因位，该基因位的值不能与同一段基因位的值相同，表示同一组任务内不可调度相同序号的AGV。

6)终止。设置最大迭代次数，当达到最大迭代次数时，终止迭代，输出最优结果。

图3交叉过程Figure 3 Chromosome crossing process

4实例仿真与分析

为验证随机调度策略的有效性，利用遗传算法设计仿真实验。其初始种群个数设置为400，交叉概率为0.6，变异概率为0.08。假设仿真实验在60 m×60 m的仓库中进行，将仓库左下角的第1个拣选台坐标位置设为(0,0)。针对一个拣选台的5批订单展开研究，设置该拣选台每批订单中的任务数量为60，其中，第1批订单中任务的位置如表1所示，系统中有10台AGV并且电量始终充足，其随机初始位置如表2所示，该拣选台的拣选人员每次完成拣货工作的时间为8 s，分货时间为6 s。首先将一批订单中的所有任务进行分组，每次呼叫3个任务，呼叫时间为上一组任务中最早到达拣选台的时间点，该订单的完成时间为所有AGV中完成各自任务耗时最长的时间。对每批订单进行10次仿真实验，取10组数据中的最小值作为AGV完成该订单中所有任务的总时间。

对随机调度策略进行仿真。图4为AGV完成所有任务总时间的迭代图，表3为所有任务的分配结果。

在实际的仓库运行过程中，通常会调用空闲的AGV来完成当前的任务以减少任务的完成时间。但在这种情况下，每次可调度的AGV数量减少，且没有考虑到AGV在拣选台的等待时间，反而会导致任务的完成时间变长，因此为了验证随机调度策略的效果，对调度空闲AGV策略进行对比仿真。调度空闲AGV策略的数学模型中增加了约束参数Yi，表示每次呼叫的任务只能由空闲的AGV来完成，只有Yi与Xi j的值同时为1时，第i台AGV才完成第j个任务。AGV是否为空闲取决于当前任务的呼叫时间点与该AGV完成上一个任务的时间点之间的差值，如式(9)所示。

表1第1批订单的任务位置Table 1 Position of the tasks of the first order

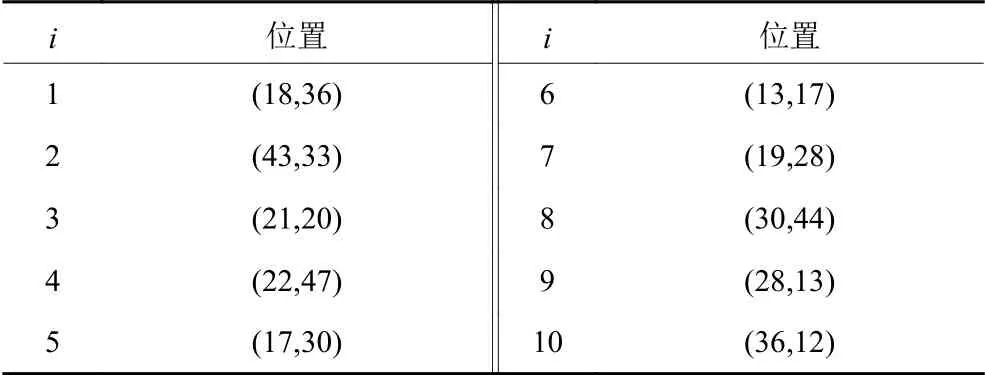
表2 AGV位置Table 2 Position of AGVs

针对以上任务，采用调度空闲AGV策略进行仿真。图5为AGV完成所有任务总时间的迭代图，任务分配结果如表4所示。

从图4和图5可以看出，随着迭代次数的增加，AGV完成所有任务的总时间不断减少，最终找到最优解。表3、表4中任务分配结果的第1个数字代表AGV的序号，后面则是该AGV依次完成的任务序号。从表中可以看出，不同的调度策略得到的任务分配结果不同，所有任务的完成时间不同。通过数值比较，本文所提出的随机调度策略的AGV完成所有任务总时间优于调度空闲AGV策略。为进一步验证随机调度策略具有更优的效率，分别采用2种调度策略对5批订单进行仿真。图6为针对5批订单采用2种调度策略下的AGV完成所有任务总时间的对比图。从图6可以看出，随机调度策略较调度空闲AGV策略拣选效率更高。

表3随机调度策略的任务分配结果Table 3 Task assignment results of random scheduling strategy

表4调度空闲AGV策略的任务分配结果Table 4 Task assignment results of scheduling idle AGV

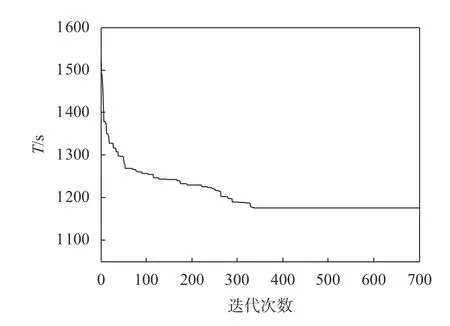
图4随机调度策略下AGV完成所有任务的总时间迭代图Figure 4 Total time to complete all tasks using a random scheduling strategy

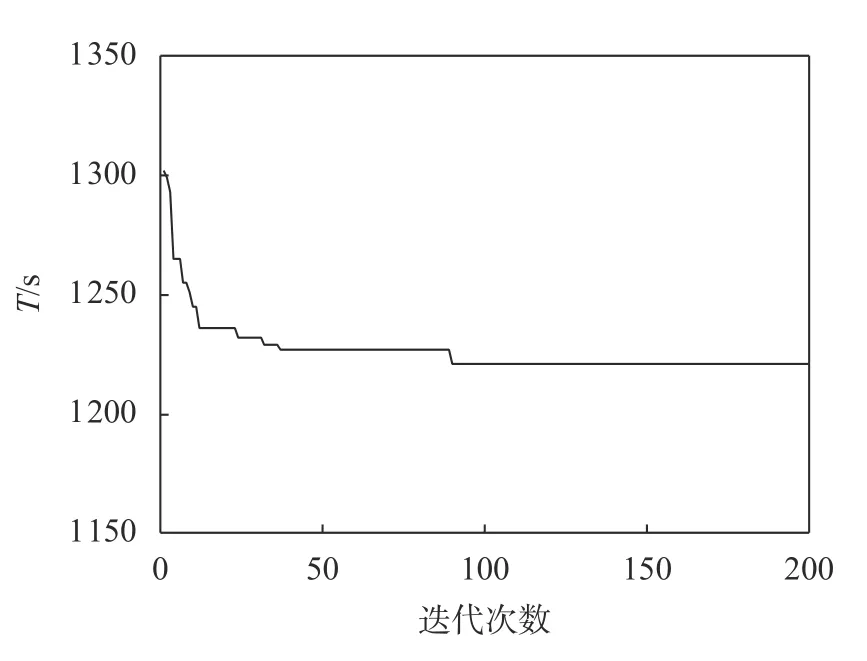
图5调度空闲AGV策略下完成所有任务的总时间迭代图Figure 5 Total time to schedule idle AGV to complete all tasks

图6 2种调度策略下AGV完成5批订单的时间Figure 6 Time for AGV to complete five orders under the two scheduling strategies

在仿真中发现，调度空闲AGV策略下，AGV可选集合中AGV的数量较少，为进一步验证以上所得出随机调度策略较优的结果是否受AGV数量的影响，将AGV的数量分别取12、14、16及18，对不同数量AGV分别进行10次仿真实验，每组最小值作为该数量AGV完成所有任务的总时间，如图7所示，对不同AGV数量情况下的2种调度策略分别进行仿真。

从图7可以看出采用随机调度策略时所有任务的总完成时间始终低于调度空闲AGV情况，说明随机调度策略优于调度空闲AGV策略。随着AGV数量的增加，采用随机调度策略，能在一定程度上提高效率，但当AGV数量高于一定值时，效率提升并不明显。对于调度空闲AGV策略，最初曲线呈下降趋势，但当AGV数量为16时，反而降低了效率，由此可以得到较优的AGV数量配置。为进一步分析曲线上升原因，考虑到所有任务的完成时间由AGV的行走时间与AGV在拣选台的等待时间组成，因此，对仿真结果中AGV的等待时间做进一步分析，如图8所示。

图7 不同AGV数量情况下采用2种调度策略的所有任务完成时间Figure 7 All task completion time with two scheduling strategies for different AGV numbers

图8为当AGV数量为16时，分别对2种调度策略的10次仿真实验结果降序排序。可以看出，采用随机调度策略时，AGV等待时间所占比例明显少于调度空闲AGV策略时AGV等待时间所占比例，并且2种调度策略的AGV等待时间占总完成时间的比例较大，进一步对等待时间进行分析。图9为分别采用2种调度策略时16台AGV的总等待时间。

由图9可以看出采用调度空闲AGV策略时，大多数AGV的总等待时间多于采用随机调度策略时AGV的总等待时间。但此图还无法说明16台AGV时调度空闲AGV策略总完成时间上升，随机调度策略时间下降减缓的现象。因此将AGV的数量分别取12、14及16，对AGV的总等待时间进行分析，结果如图10所示。

图9 2种调度策略下AGV总等待时间Figure 9 Total waiting time of each AGV under two scheduling strategies

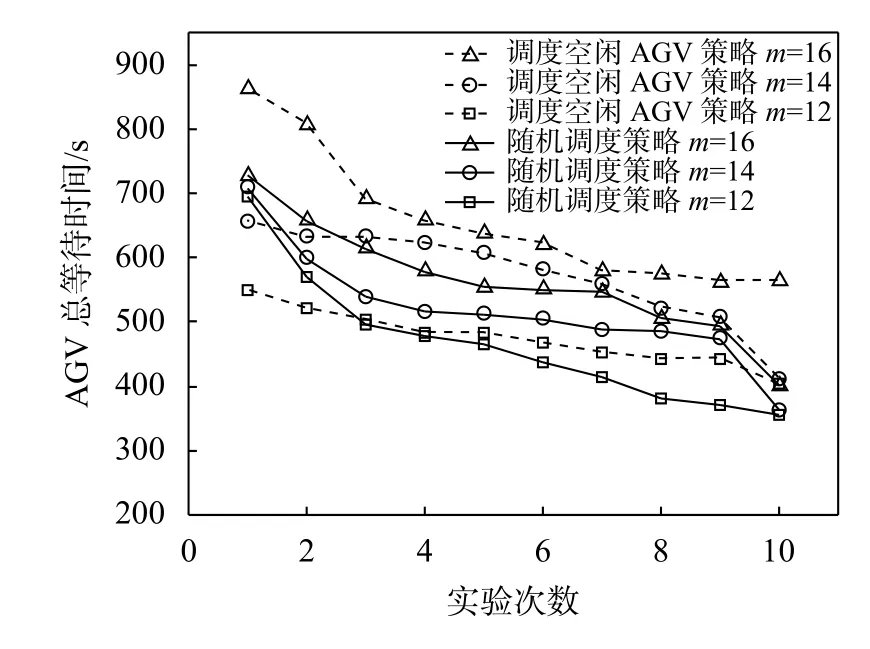
图10不同数量AGV情况下2种调度策略AGV总等待时间Figure 10 Total waiting time of AGV of two scheduling strategies with different numbers of AGV

图10为当AGV数量不同时，2种调度策略下AGV的等待时间，将每种情况的仿真结果降序排序。当AGV数量相同时，实线的大部分点低于虚线点，表示采用随机调度策略时，AGV的总等待时间低于采用调度空闲AGV策略时AGV的总等待时间，间接说明了采用随机调度策略时所有任务的完成时间少于调度空闲AGV时所有任务的完成时间的原因。随着AGV数量的增加，2种调度策略的AGV总等待时间增加，但采用调度空闲AGV 策略时，AGV总等待时间的增量大于采用随机调度策略时AGV总等待时间的增量。

图11为AGV数量增加时，10次实验的2种调度策略下AGV的平均等待时间与平均行走时间。随着AGV数量的增加，2种调度策略的AGV总等待时间增加，但采用随机调度策略时AGV等待时间的增量小于采用调度空闲AGV策略时的增量，AGV数量为16时，采用调度空闲AGV策略的AGV总等待时间的增量大于AGV总行走时间的减少量，因此此时AGV完成所有任务的总时间会增加。这就解释了图7中采用调度空闲AGV策略时，AGV数量增加反而会导致所有任务的总完成时间增加的结果。

图11 AGV数量增加情况下2种调度策略的AGV等待时间与行走时间Figure 11 Waiting time and traveling time of AGV of the two scheduling strategies when the number of AGV increases

综上分析，随着AGV数量的增加，可以调度的AGV数量增加，AGV将货架搬运至拣选台所花费的时间减少，意味着每次呼叫的时间提前，这导致了排队等待的AGV数量增加和所有AGV等待时间的增加。由于采用调度空闲AGV策略时，随着AGV数量的增加，所增加的AGV的等待时间大于AGV搬运任务所花费时间的减少量，因此完成所有任务的总时间增加，而采用随机调度策略时，随着AGV数量的增加，所增加的AGV等待时间小于AGV搬运任务所花费时间的减少量，因此完成所有任务的总时间减少。当AGV数量一定时，随机调度策略与调度空闲AGV策略相比，每次可以调度的AGV数量较多，进而可以得到全局最优解。通过以上仿真结果进行分析，随机调度策略比调度空闲AGV策略效率更高。当采用随机调度策略时，随着AGV数量的增加，系统效率的提升并不明显，所以，考虑AGV的投入成本较高，配置14台AGV完成以上任务比较合理。

5结论

在“货到人”拣选系统中，为了提高系统的拣选效率，本文从AGV调度策略角度进行优化，提出了一种随机调度策略。以耗时最长的AGV的完成任务时间最短为目标函数，考虑AGV在拣选台的排队等待时间，建立随机调度策略的数学规划模型，通过遗传算法进行求解。仿真实验结果表明，本文所提出的随机调度策略减少了AGV在拣选台的排队等待时间，提高了拣选效率。通过不同数量AGV拣选效率对比实验仿真发现，AGV数量的增加对最终效率提升的贡献有限。该结果对拣选系统中AGV的数量配置具有一定的指导作用。本文所提随机调度策略在得到全局近似最优解的同时解决了AGV调度与拣选系列问题，为拣选系统的设计与应用提供了参考。