考虑生产过程时间的柔性作业车间调度优化

2020-05-03李峥峰于小忠张国辉崔陆军

工业工程 2020年2期

李峥峰，于小忠，张国辉，崔陆军

(1.中原工学院机电学院，河南郑州450007；2.郑州航空工业管理学院管理工程学院，河南郑州450015)

柔性作业车间调度问题(flexible job shop scheduling problem，FJSP)中有多个设备可以完成工件加工任务，即某工件的某道工序可以由多台设备完成加工任务，其加工时间因加工设备的差异而有所差别。在柔性作业车间中，工件工艺的加工设备具有更多选择性，其加工具有更高的柔性，但也增加了求解规模和复杂程度。在实际应用中，柔性作业车间具有更普遍的意义，其调度问题的研究对指导实践生产具有重要的意义。

FJSP描述如下。在i台设备{M1,M2, ···,Mi}上加工j个工件的多道工序，每个工件至少有1道加工工序，其工序的加工顺序是确定的。每道工序有多台可选加工设备可以完成该工序的加工工艺，同一道工序的加工时间由于所选机器的差异而有所不同。目前，仅考虑加工时间因素的柔性作业车间调度问题研究相对比较成熟，并获得了大量的研究成果。由于考虑辅助时间更加贴近车间调度的实际应用，近年来考虑辅助时间的研究逐渐引起了大家的重视。制造企业调查统计表明[1]：在制造过程中，非加工时间占整个生产时间的90%以上。这说明辅助时间对生产效率有极其重要的作用，有必要对辅助时间进行深入的研究。

在柔性作业车间调度中，目前已经有部分学者对辅助时间的作用加以重视，开始考虑某种辅助时间因素的一种或几种，如调整时间、运输时间和故障时间等对车间调度的影响[2-9]。文献[2]对考虑故障时间的柔性作业车间鲁棒调度进行了研究。文献[3]对维修任务调度进行了研究。文献[4]研究了预防性设备维护的柔性作业车间调度问题。文献[5]对考虑调整时间的作业车间调度问题的国内外研究进行了综述，对批量调整时间、非批量调整时间、顺序相关调整时间、顺序无关调整时间的作业车间调度问题研究进行了分析。文献[6]从顺序相关调整时间(调整成本)、顺序无关调整时间(调整成本)、组调整时间等方面对考虑调整时间调度问题的单机、并行机、流水车间、装配流水车间、作业车间、柔性作业车间和开放车间等进行了分析综述。文献[7]对近20多年的柔性作业车间调度技术进行了综述，从调度目标和求解方法层面进行了分析，相对于理论研究，其实际应用研究相对缺乏。文献[8]研究了考虑运输时间的柔性作业车间调度问题，建立了关键链优化方法。文献[9]研究了带准备时间的作业车间分批排序问题。

虽然上述研究取得了一定的成果，但大多考虑某一种或几种辅助时间因素，没有从车间生产系统层面分析辅助时间，甚至某些时间划分存在某种重叠、模糊、不一致，比如等待时间包括故障时间、机器占用等待时间、工件运输等待时间等。本文从车间调度的角度出发，分析生产中的多种非加工时间因素，从工件生产过程实践出发，建立车间生产过程的时间模型，在此基础上建立考虑多种辅助时间的FJSP调度模型，并设计混合遗传算法求解。

1柔性作业车间生产过程时间模型

基于不同的出发点，对生产中各个时间的定义会有重叠，这影响了调度的理论研究及其应用。有的时间定义的对象不同，比如以工件为对象的加工时间，以机器设备为对象的故障时间；有的时间出发点不同，比如等待时间包括故障时间、机器占用等待时间、工件运输等待时间等。只有进一步细化区分这些辅助时间，才能使调度理论研究更好应用于车间生产实践。

一般意义上，等待时间为工件前后工序加工间的停顿时间。从调度理论研究的角度出发，把等待时间分解为工件运输时间、机器调整时间、机器故障时间和机器占用时间等4个部分。其中，其他工件的加工时间包含机器占用时间，而工件运输时间、机器调整时间、机器故障时间需要进行单独考虑。为更加符合柔性作业车间生产情况并符合调度研究的需要，生产过程时间参数定义明确没有重叠，如图1所示。具体划分如下。

加工时间指生产设备完成工件某道工序加工所需的时间。根据工艺和加工设备的不同，不同工序加工时间不同。

准备时间：在通常情况下，假设工件准备就绪随时可以加工，即准备时间为0。

等待时间通常为工件前后工序加工停顿的时间。本文定义机器被其他工件加工占用而导致本工件加工停顿的时间为等待时间，并从中分离出运输时间、故障时间、调整时间进行单独研究。该等待时间不影响完工时间的优化。

故障时间为由于机器设备故障导致工件不能正常加工的时间。一般从机器不满足工件加工质量要求开始计时，经维修、修复、重新启动直到正常待机开始正常加工为止。

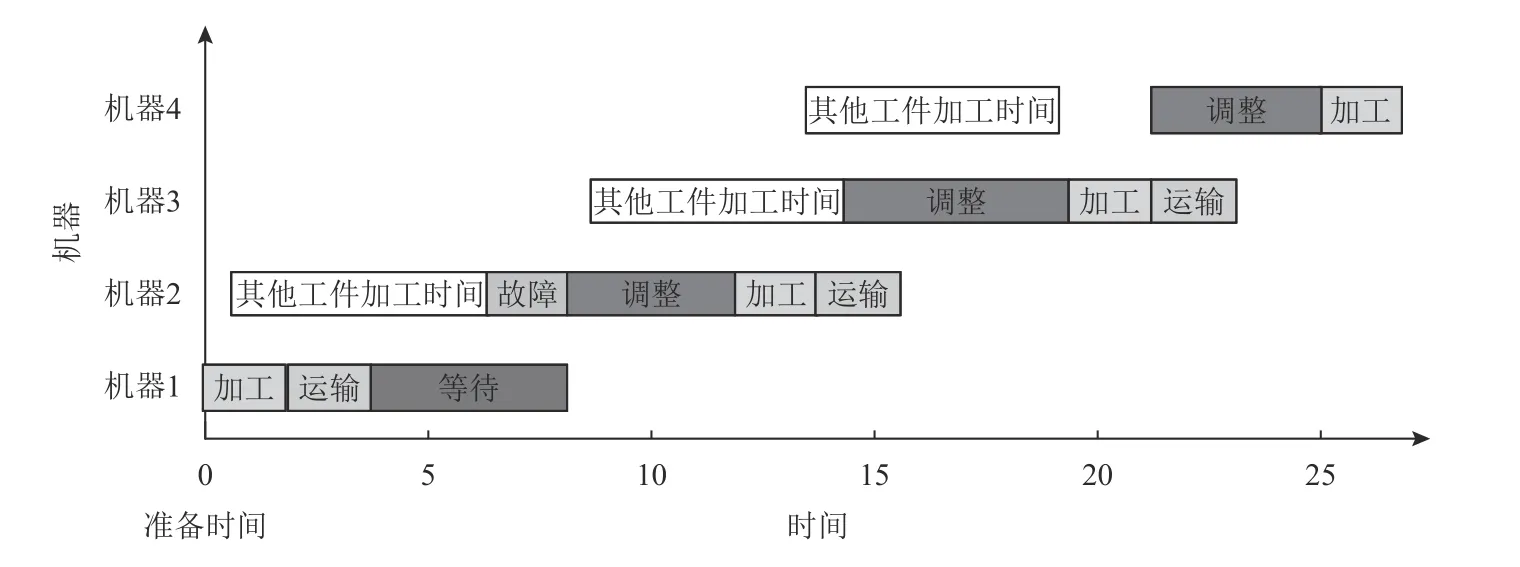
图1生产过程时间模型Figure 1 The model of production process time

调整时间是指由于加工设备上加工的工件工序的变换，需要进行模具、家具、装卸、启动等操作而产生的时间，可以分为顺序相关和顺序无关调整时间2类。

运输时间是指移动搬运工件所产生的时间。

2基于生产过程时间的FJSP建模

经过上述生产过程时间模型的分析，单独分离调整时间、故障时间以及运输时间，来研究柔性作业车间的优化调度问题。

考虑调整时间的工序顺序性质，建立一个三维调整时间表，其中第1维表示当前要加工的工序，第2维表示上道加工工序，第3维表示所有机器设备。根据第3维的设备确定加工设备，然后在第1维和第2维组成的平面上可以找到任意2个该设备上加工的工序及上道加工工序，从而可以确定其调整顺序相关时间。针对顺序无关调整时间，可以选择相同的工序即对角线上的时间表示。

在实际生产活动中，对某类型工件而言，其体积、重量、运输方式比较固定，可以假定与此相关的初始时间为常数Tc。此时，运输时间为

其中，j为工件号，h为工序号，f(d)为运输距离的正比例函数，参考调整时间和加工时间大小，可以直接用设备的间隔数表示距离。

设备的故障时间是不确定和随机的，根据车间生产的实际经验并参考工序加工时间的大小，设备以一定概率发生故障。

考虑加工时间、调整时间、故障时间、运输时间以及综合调整时间和运输时间、故障时间，以工件最大完工时间最小化为目标的柔性作业车间调度模型如下。

其中，工件每道工序的开始时间和完工时间分别为

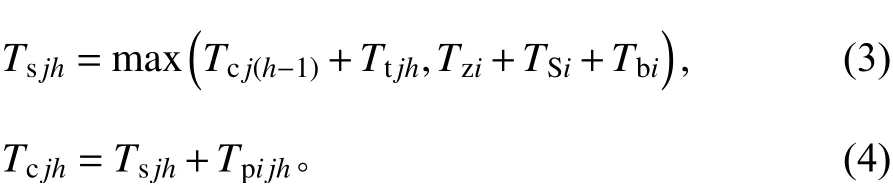
其中，Tsjh为工件j工序h的加工开始时间；Tcjh为工件j工序h的完工时间；Tzi为设备i的空闲时间，即上个工件工序的完工时间；TSi为工件j工序h在设备i上的调整时间；Tbi为设备i的故障时间，Tpi jh为工件j在设备i上进行工序h加工的时间。

优化过程中，还需要满足以下约束条件：1台机器某时刻只能加工1个工件；1个工件某时刻只能在1台设备上加工；工件工序加工过程中不中断且无故障；工件工序按工艺先后顺序加工；工件的首道工序到设备的运输时间相同；设备故障后进行调整，不考虑调整后设备故障；首工序考虑调整时间。

3求解FJSP的混合遗传算法设计

选择工件的加工机器和机器上工件的先后加工顺序，是解决FJSP调度问题的2个问题。前者是机器选择问题，解决机器上加工哪些工件工序的问题；后者是工序排序问题，解决工序在所选机器上加工的次序和开工时间问题。在FJSP问题的遗传算法研究的基础上[10-13]，设计了如图2所示的混合遗传求解算法。

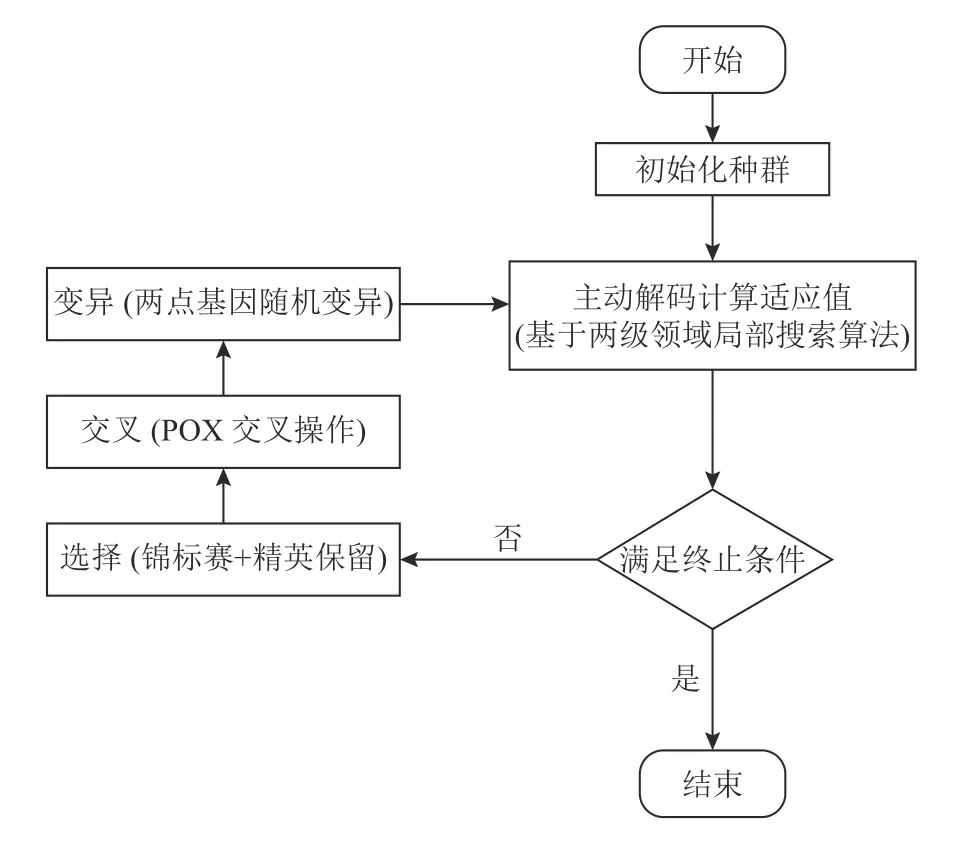
图2混合遗传算法流程图Figure 2 Flow chart of hybrid genetic algorithm

3.1编码

编码采用分段整数编码方式，包含如下2个部分。

1)工序排序部分。工序基因数目等于所有工件工序的总和。每一位基因用工件号码表示，即某工件有几道工序，该工件号就在染色体中出现几次，出现的序次就是其工序数。

2)机器选择部分。机器基因数目与工序部分基因数目相等，其基因位是相应工序的可加工机器号。

3.2解码

工序排序染色体部分和机器选择染色体部分组成FJSP的染色体，考虑到两部分染色体的编码含义不同，在解码过程中分别对其进行解码，并最终生成机器上加工工序先后加工顺序的活动调度。首先，逐位解码工序部分染色体基因，先确定基因位的工件工序含义；然后，按照对应的机器选择部分染色体编码基因，选择其加工机器，生成工序在所选机器上的活动调度；最后，对所有工件工序进行先后排序得到调度结果。其具体步骤如下。

步骤1读取染色体的1位基因，计算其在染色体出现的位置和次数，解码为工件j的第h道工序Ojh。

步骤2从机器选择染色体对应位置确定其加工机器Mi，并获取加工时间Tpi jh。

步骤3生成机器加工的活动调度，即从起始时间开始依次判断机器上已排序加工工件的时间间隔是否可以插入该工件的加工。

1)设该工序Ojh插入位置为k，k=0，表示插入到设备加工工件顺序的首位，此时机器空闲时间Tzi=0；

2)根据式(3)计算Tsjh和式(4)计算Tcjh。

3)判断后面是否还有工件。若没有，则表示插入到最后位置，结束判断；否则继续下一步。

4)判断是否满足该工序Ojh完工时间不大于k位置后工件的开工时间。如满足，则表示可以插入该工件前，结束判断；否则继续下一步。

5)判断下一个工件间隔是否可以插入，即把插入位置向后移动1位，k=k+1，获得其完工时间Tck，同时该机器空闲时间Tzi=Tck，转至2)，重新计算Tsjh和Tcjh。

4)工序部分染色体的基因是否解码完毕。是则解码过程结束；否则转步骤1继续。

至此，完成FJSP染色体的解码，生成FJSP工件加工的活动调度，并可以排出每台加工机器上加工工件的顺序，从而得到所有工序加工的开始和结束时间。

某例染色体解码后生成活动调度如图3所示。其中，Oef、Ojh、Oml、Ouv表示设备Mi上加工的不同工件的某道工序，TSijh表示设备Mi上加工工件j的h工序需要的调整时间，Tbi表示设备Mi的故障时间。

图3染色体解码生成活动调度Figure 3 The active scheduling of chromesome encoding

3.3 FJSP的初始化

FJSP染色体包含工序排序问题和机器选择问题，其初始化要同时解决这2个问题。随机初始化具有样本多样性的优点，有利于GA初始种群的多样化并且分布于整个解空间。所以本文采用随机初始化染色体方式。

工序染色体生成方法如下。

1)原始代码空间由所有工件的工序组成，工序由工件号表示，空间中工件号数量与其工序数量相同。

2)随机选择代码空间工件号作为工序基因，同时在原始空间去除该代码，直到生成工序部分染色体的全部基因。

机器染色体生成方法：染色体基因位表示工件工序加工机器序号，该数字的选择是可选机器序号随机产生的。

1)从工序染色体第一位基因开始，选出工件的工序。

2)从工序可选机器集随机选出机器代码作为机器染色体基因。

从当年“三天建一层楼”的“深圳速度”，到今天破旧立新的自贸区探索，都是“一个汗珠摔八瓣”拼出来的。不做光说不练的“假把式”，争当脚踏实地的“实干家”，“撸起袖子加油干”就是成就改革事业的“硬道理”。

3)选择工序染色体的下一位基因，重复执行2)，直到所有工序基因选择加工机器，即完成了所有加工机器的选择。

3.4交叉操作

3.4.1工序排序部分

采用POX方法交叉操作，可以保持父代染色体的优良特征[10]。

1)工件集{J1,J2,···,Jn}采用随机方式进行工件抽取，从而得到工件子集set1和set 2；

2)分别对2个工件子集生成其子代C1/C2，如图4(a)所示。

对工件子集set1生成子代C1，依次按父代染色体基因位进行顺序复制。如果父代染色体P1的基因位是set1所包含的工件，则保持位置和顺序不变，复制到子代C1；然后根据C1空白位置，按顺序依次复制父代染色体P2中的非set1工件的基因位到C1。

同样的方式，对工件子集set 2生成子代C2。

3.4.2机器选择部分

1)在染色体长度N0内随机产生整数r表示交叉的基因数目；

2)在长度N0范围内随机产生r个不等的整数表示交叉基因的位置；

3)根据步骤2)产生的交叉基因的位置，复制该位置的父代P1基因到子代C1相应位置，然后根据C1染色体基因的空白位置，把对应位置的父代P2基因复制到子代C1相应基因位置；

4)同样地，复制相应位置的父代P2的基因到子代染色体C2，并把其他位置复制父代染色体P1的对应基因，得到子代染色体C2。

如图4(b)所示，图中随机生成灰色基因位，C1复制相应位置P1中的基因，C1空白位置基因按顺序依次复制P2白色基因位，获得新的染色体C1。

3.5变异操作

工序染色体的变异操作采用随机互换两点基因变异。

对机器选择染色体部分，为较好保持机器顺序信息，本文采用如下的变异方法。

1)随机选择一位基因，设置为加工时间最短的机器号；

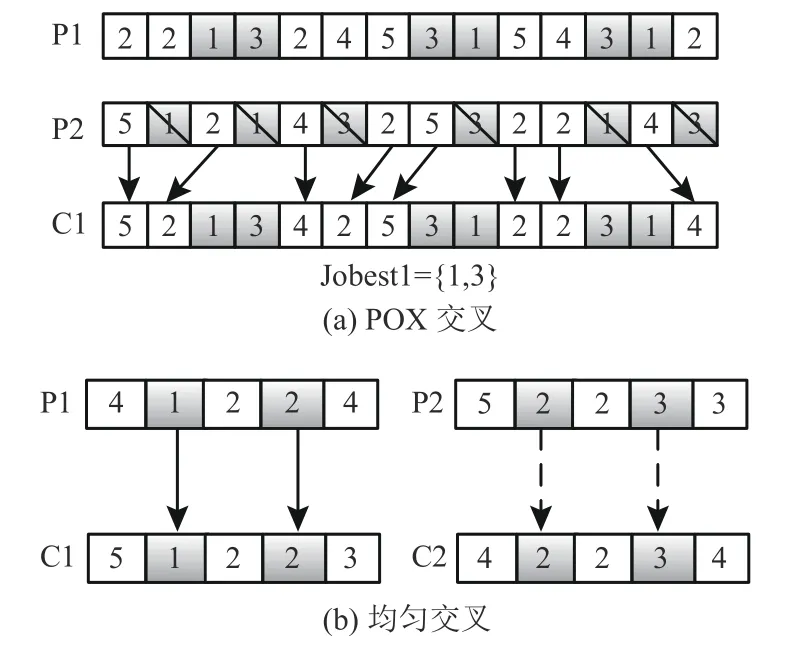
图4交叉操作Figure 4 Crossover operation

2)再随机选择一位基因，设置为可选的随机的机器号。

3.6 局部搜索

采用参考文献[13]中的两级邻域搜索方法，即通过改变工件的可选设备进行跨机器移动工序和移动同机器上工序的前后加工顺序实现两级邻域搜索方法，对适应值前10%的进行局部搜索，提高解的质量。

3.7 选择操作

采用锦标赛方法和精英保留策略，随机选择3个适应度最高的染色体到交叉池中，如果适应值相同，优先选择拥挤距离大的进入交叉池，直到交叉池染色体全部选择完成后，结束选择循环操作。

4测试实例

采用VC++编程，程序在酷睿i7，CPU主频2.8 G，内存32 G的笔记本上运行。初始种群个数为200，交叉概率为0.8，变异率为0.01，迭代100次，采用保优策略。采用上述遗传算法对经典FJSP问题用例MK01、8P和10P问题进行了测试对比。这3个用例中MK01和8P代表部分柔性作业车间，其工件工序数和可加工设备不同。10P代表了完全柔性作业车间，其工件工序数相同且可加工设备相同；而8P和10P的工件工艺加工时间相似，可以采用相同的调整时间、运输时间、故障时间进行性能改进效果对比。参考所选经典用例工件的加工时间，用例的调整时间可以采用小于3的随机数；运输时间中常数Tc假定为1；f(d)直接用设备数间隔表示；设备以10%的概率产生4以内的随机数为故障时间。测试结果如表1所示。表中各列中实例问题表示测试用例；最优解表示仅考虑加工时间的最优完工时间；辅助时间表示考虑了哪些细分辅助时间，改进前数据表示优化时不考虑该辅助时间但实际生产具有辅助时间的情况下的最大完工时间；改进后数据表示优化时考虑辅助时间优化的最大完工时间；优化百分比为改进后完工时间相对改进前完工时间的减少百分比。测试结果显示，相对不考虑辅助时间进行车间调度优化，考虑辅助时间的车间调度优化，其性能有明显差别。以8P为例，存在辅助时间的情况下，6种情况的调度甘特图对比如图5～10所示，可以明显看出调度结果有很大不同，并且完工时间有明显的改进。

表1柔性作业车间调度测试结果Table 1 The test results of flexible job shop

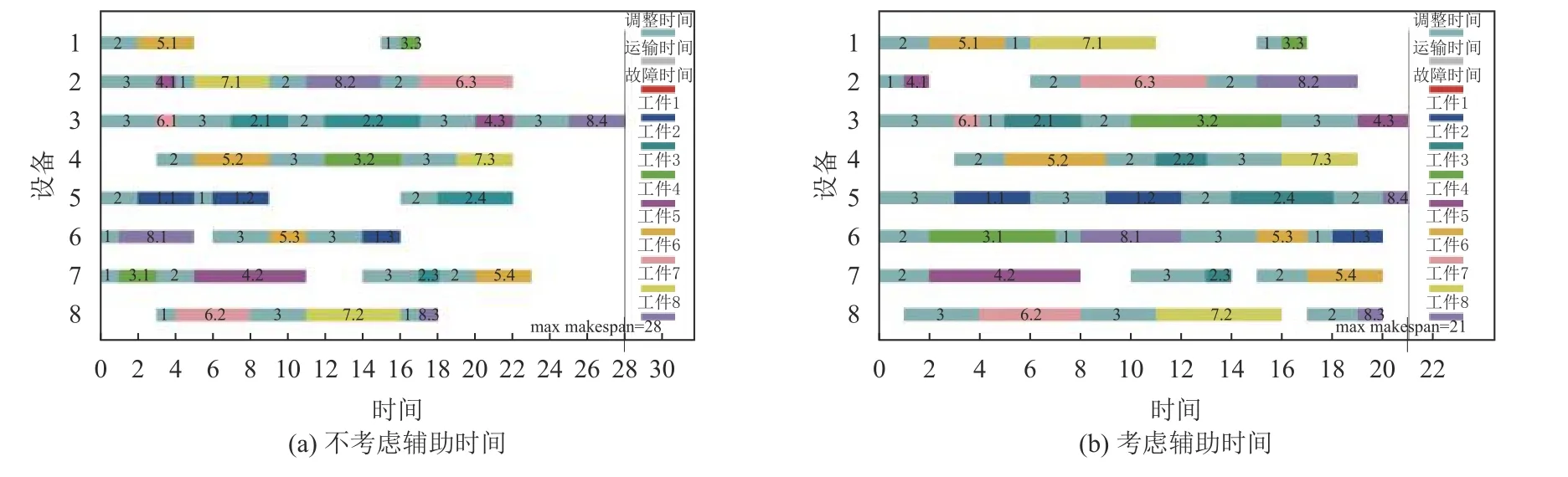
图5是否考虑顺序无关调整时间优化的调度甘特图Figure 5 The Gant chart of scheduling with sequence-independent setup time or not

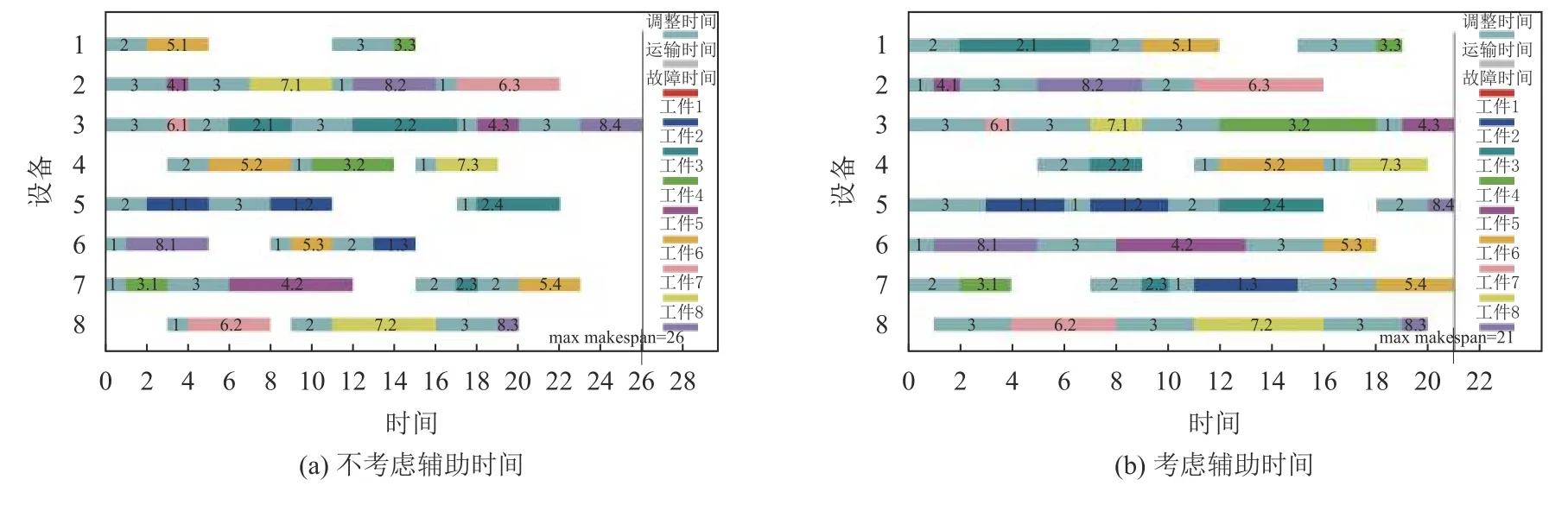
图6是否考虑顺序相关调整时间优化的调度甘特图Figure 6 The Gant chart of scheduling with sequence-dependent setup time or not

图7 是否考虑运输时间优化的调度甘特图Figure 7 The Gant chart of scheduling with transportation time or not

图8 是否考虑故障时间优化的调度甘特图Figure 8 The Gant chart of scheduling with failure time or not

5小结

本文分析了柔性作业车间生产过程中的各个时间段，建立了生产过程时间模型，研究了柔性作业车间调度问题，并设计基于工序整数编码和机器整数编码的混合GA 算法来求解FJSP。最后采用FJSP的典型用例，对考虑调整时间、故障时间以及运输时间因素的柔性作业车间调度问题模型进行了验证、对比、分析和总结。结果显示，辅助时间对优化性能和结果都有明显影响，在进行车间调度优化研究时应该给予充分考虑，从而使得理论调度在实践中得到良好应用。