基于Duffing振子的微弱信号参数估计

冀常鹏，许素娜，冀雯靖

(1.辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105；2.辽宁省露天矿山装备工程研究技术中心，辽宁 阜新 123009；3.辽宁工程技术大学 研究生院，辽宁 葫芦岛 125105；4.香港中文大学(深圳) 理工学院，广东 深圳 518172)

0 引 言

随着信息技术的迅速发展，检测被强噪声覆盖的微弱信号[1]逐渐成为一个很重要的课题。Brix[2]首先提出将混沌理论应用在微弱信号检测方面，之后许多专家开始对其展开研究并获得了诸多成果。在洛伦兹振子、Duffing振子、Rossler振子等混沌振子[3]中，Duffing振子为最典型的一种，因具有初始条件敏感性、零均值噪声免疫性[4-7]等特征被广泛应用在微弱信号检测领域。

文献[8]将待测信号经过预处理后加入到Duffing振子系统进行检测，实验结果表明，此方法能够提高检测效果，但未对微弱信号的参数进行估计；文献[9]所构造的检测系统仿真模型，能够有效检测出淹没在强噪声中的微弱正弦信号，获得相对满意的仿真效果，但临界阈值是通过直接观察相轨迹图获得的，缺乏量化判断依据；文献[10]提出将Duffing振子检测系统中的非线性恢复力用-x5+x7替换，同时提出尺度变换方法，但其所用的单Duffing振子仅能检测出和内置周期驱动力频率非常接近的信号；虽然文献[11]利用Duffing振子阵列能够对任意微弱信号的频率进行估计，但所需振子数量多，增加了复杂度。

针对上述文献不足，提出结合Duffing振子和频谱分析的微弱信号频率检测方法，在得到频率的基础上，给出可以估计微弱信号幅度和初相位的方法，通过Matlab仿真平台对所提方法进行验证并完成对微弱信号的有效检测和高精度参数估计，仿真过程中用Lyapunov指数方法观察检测系统是否发生相变。

1 Duffing振子检测原理和相变判据

1.1 Duffing振子检测原理

用于微弱信号检测的某一Duffing振子[12]为

(1)

(1)式中：k是阻尼系数；-x(t)+x3(t)是非线性恢复力；fcos(ωt)是内置周期驱动力，f和ω分别为其幅值和频率。

经过理论分析和大量的仿真实验可知(1)式所构成的检测系统对微弱方波信号较为敏感，对微弱正弦信号不太敏感，由于我们主要对微弱正弦信号进行检测，因此，改进(1)式的-x(t)+x3(t)由-x3(t)+x5(t)代替，此时动力学方程为Homes-Duffing方程

(2)

固定k值，当f=0时，可知检测系统的相平面有3个奇点，原点(0,0)是其鞍点，(+1,0)，(-1,0)为其2个中心相点，检测系统的相点最终会停留在其中一个，这取决于系统的初始参数；当f≠0时，检测系统会呈现复杂的动力学形态，若f很小，检测系统的相点会围绕(+1,0)或(-1,0)做衰减周期运动，当f增加时，检测系统会依次呈现出同宿轨道、倍周期分叉状态，直到f大于fc(混沌阈值)时，检测系统开始出现混沌状态，检测系统在之后的一段时间都保持混沌状态，直到f即将增加到fd(临界阈值)时，检测系统呈现图1a的临界混沌状态，f≥fd时检测系统呈现图1b的大尺度周期状态。

传统Duffing振子系统检测原理为：首先令内置周期驱动力幅值f=f0(f0略小于fd)，此时检测系统呈现临界混沌状态，若f再增加很小的Δf，检测系统会转为大尺度周期状态；然后将待测信号作为内置周期驱动力的补充加入到检测系统，若待测信号中含有与内置周期驱动力同频的微弱正弦信号且叠加后幅值大于等于fd，则检测系统会发生相变，即待测信号中存在微弱正弦信号，否则不存在；检测过程中常用直接观察法判断系统是否发生相变。

传统Duffing振子检测系统虽然可以有效检测出某些微弱正弦信号，但存在以下缺点。

1)若使用单一Duffing振子，则仅能检测和内置周期驱动力频率非常接近的微弱正弦信号，即微弱正弦信号频率必须事先知道。当微弱正弦信号频率未知时，虽然可以利用Duffing振子阵列完成检测，但增加了复杂度。

2)目前判断检测系统是否产生相变的常用方法为直接观察法，该方法由于是通过肉眼观察，故存在一定的主观性、效率低且容易发生误判，很难满足实际工程的需求。

基于以上相关问题，提出将频谱分析和Duffing振子相结合的方法来估计微弱正弦信号的频率，并利用Lyapunov指数方法[13]作为检测系统产生相变的依据。在该基础上完成了微弱正弦信号幅度和初相位的估计。

1.2 相变判据

混沌检测是通过Duffing振子系统产生相变来检测微弱信号的，因此，准确判断检测系统的状态至关重要。虽然Melnikov方法[14]可以作为产生相变的判据，但精确度不是很高，同时为避免直接观察法的缺点，采用Lyapunov指数方法来判断检测系统是否产生相变。

Lyapunov指数方法判断Duffing振子系统状态的原理为若检测系统的最大Lyapunov指数值Lyapunovmax>0，代表系统呈现混沌状态。若检测系统的Lyapunovmax<0，则代表其呈现大尺度周期状态，因此，当Lyapunovmax>0跳变为Lyapunovmax<0时所对应的内置周期驱动力幅值为检测系统临界阈值fd。

利用Wolf法求时间序列的Lyapunovmax的基本思想是对于混沌时间序列x(t)，对其进行m维的相空间重构，即吸引子上的某点可以由{x(t),x(t+τ),…,x(t+[m-1]τ)}获得，假如选择点{x(t0),x(t0+τ),…,x(t0+[m-1]τ)}作为基准轨道上的初始点，然后再选择距离该点最近一点作为邻近轨道的初始点，用L(t0)表示它们之间的距离。当时间为t1时，距离变为L′(t1)，为避免其溢出，再选择另一数据点，但应满足2个条件：①与基准轨道上的对应演化点距离要非常小；②基准轨道上对应点到新数据点和到旧数据点所构成的2向量夹角也必须非常小。若不存在满足以上2个条件的点，就继续使用原数据点，不进行更新，直到基准轨道取遍全部的数据，因此，最大Lyapunov指数λmax为

(3)

(3)式中，M是替代的总步数。

2 改进方法

2.1 频谱法Duffing振子检测频率

频谱法Duffing振子检测频率的思想是在传统Duffing振子检测系统基础上，摒弃内置周期驱动力，将待测信号直接输入到检测系统，然后对检测系统的输出信号作频谱分析获得微弱正弦信号的频率。

结合传统Duffing振子所构造的检测模型为

(4)

(4)式中，s(t)=acos(ωt)+n(t)是待测信号，其中，n(t)是高斯白噪声。因为没有内置周期驱动力，此时检测系统只由待测信号驱动，所以不用考虑微弱正弦信号与内置周期驱动力是否同频，故可以检测任意频率的微弱正弦信号，避免了利用多振子阵列检测增加复杂度的问题。为满足当仅有待测信号存在时，检测系统能够发生相变，待测信号幅度a需大于临界阈值fd。

在进行频谱分析时，有2种方法可以选择，分别为傅里叶分析方法和小波分析方法[15]。由傅里叶分析方法得到的频谱图，待测信号的幅度和其他谐波分量幅度之间存在明显的差异，因此,能求出待测信号频率(即微弱正弦信号的频率)。

将待测信号输入到Duffing振子检测系统，对输出量作傅里叶变换，得到以频率为横坐标，各谐波幅度值为纵坐标的频谱图，由频谱图能求出待测信号的频率。

对所提方法进行实验验证，(4)式中k值取0.5，ω值取10 rad/s，参数设置完成后开始仿真，傅里叶分析通过编程实现，并以坐标形式给出实验数据，检测系统的输出信号频谱图如图2。

2.2 待测信号幅度和初相位估计方法

由2.1节可完成待测信号频率的估计，在此基础上，继续对待测信号幅度和初相位进行估计，此时Duffing振子检测系统内置周期驱动力不置零，其频率设置为待测信号频率，然后结合Lyapunov指数方法求出临界阈值fd，该方法检测模型为

(5)

(5)式中：f0cos(ωt+θ)为检测系统内置周期驱动力；acos(ωt+φ)+n(t)是待测信号。此时,检测系统呈现临界混沌状态，将含有与内置周期驱动力同频的微弱信号加入到检测系统，检测系统会呈现大尺度周期状态。通过理论研究(5)式的Duffing振子进入大尺度周期状态的条件，若能发生相变，则(5)式中总的周期驱动力幅值应满足

(6)

若用fm代表检测系统刚好发生相变时所对应的内置周期驱动力幅值，则

(7)

(7)式中，fm，fd均可得到，若还可以建立一个有关a和φ的类似(7)式的方程，则通过解二元方程组可完成对待测信号的幅度和初相位的估计。以此为出发点，通过改变检测系统的内置周期驱动力的初相位得到2个方程组。具体思想是首先用频谱法Duffing振子在完成待测信号的频率估计后，然后设置(5)式中的检测系统参数，将待测信号分别输入到内置周期驱动力初相位为0和π的Duffing振子检测系统中，求出这2个系统发生相变时所对应的内置周期驱动力幅值，分别用f1和f2表示。结合(7)式得到的2个方程组为

(8)

解方程组(8)可得

(9)

由(9)式能求出a和φ，至此完成了对待测信号的频率、幅度和初相位的估计。

3 仿真实验和结果分析

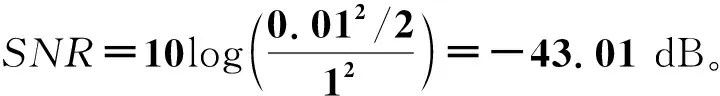
若对系统的输出信号用离散傅里叶变换(discrete Fourier transformation, DFT)算法进行频谱分析，则复杂度为序列长度的平方，即o(n2)。对DFT进行改进，形成一套高效计算方法，即快速傅里叶变换算法(fast Fourier transformation, FFT)。其思想是将长序列分解为若干短序列进行DFT计算，然后通过若干旋转因子的复数乘法和复数加法合成最终的结果。FFT算法中，若序列长度是2的幂次，可将序列长为N的DFT分割为2个长为N/2的子序列的DFT，称为基2-FFT。快速傅里叶变换算法仅需要o(nlogn)的计算复杂度，在此，利用FFT对系统的输出信号进行频谱分析。

将待测信号s1(t)，s2(t)和s3(t)分别加入到内置周期驱动力为0的Duffing振子检测系统，对其输出信号作频谱分析。给出这3组实验利用快速傅里叶变换算法得到频谱图的运行时间，如表1，输出信号的频谱图如图3。

由图3并结合2.1节相关知识对待测信号频率进行估计，同时利用Duffing振子阵列方法对待测信号s1(t)，s2(t)和s3(t)进行检测，根据这3个待测信号的频率范围，将第1个振子频率取1，第2个振子频率取1.03，即后面振子频率为其前一个振子频率的1.03倍，依次类推，因为检测频率在1～5 rad，由1.0354=4.934，1.0355=5.082，故需设置55个振子。

表1 本文算法检测时间Tab.1 Algorithm detection time in this paper

通过观察时序图,发现其中3组间歇混沌周期最长，分别为第1个和第2个振子、第23和24振子和第46和47个振子，如图4。

由于第1个和第2个振子分别所对应的间歇混沌周期大致相等，因此，取它们对应频率的平均值作为待测信号的近似值，同理，计算第23和第24个振子以及第46和第47个振子所对应频率的平均值。最后将频谱法Duffing振子和Duffing振子阵列方法对待测信号频率估计结果进行对比，如表2。

由表2可知，Duffing振子在信噪比为-43.01 dB的条件下仍能有效检测出微弱正弦信号，在对信号频率进行估计时，频谱法Duffing振子和Duffing振子阵列方法相比具有较高的精度，相对误差仅为10-3，复杂度低，易操作等优点。

表2 2种方法频率估计结果Tab.2 Two methods of frequency estimation results

在得到待测信号的频率估计值后，继续对待测信号的幅度和初相位进行估计，以待测信号s1(t)为例，待测信号s2(t)和s3(t)检测原理与s1(t)相同，仅需将检测系统的内置周期驱动力角频率设置为2.000 566 rad/s和3.998 619 rad/s。

具体实现步骤如下。

步骤1 将Duffing振子检测系统的内置周期驱动力角频率设置成1.000 911 rad/s，及其他系统参数设置完成后利用Lyapunov指数方法得到临界阈值fd。

步骤2 将待测信号s1(t)作为内置周期驱动力的补充，输入初相位分别为0和π的Duffing振子检测系统。

步骤3 通过编程达到以下功能：将步骤2中所得到的输出时间序列，利用FFT算法来计算其平均周期；通过C-C方法确定其延迟时间和嵌入维数并进行相空间重构；最后利用重构的相空间，再次计算检测系统的最大Lyapunov指数，若其值大于0，则调整内置周期驱动力的幅值，并重新计算调整后的最大Lyapunov指数，直到最大Lyapunov指数刚好由大于0转变为小于0，记录此时所对应的内置周期驱动力幅值f。

步骤4 初相位为0和π的检测系统发生相变时所对应的内置周期驱动力幅值分别记为f1和f2，代入(9)式后，得到待测信号s1(t)的幅度和初相位的估计值。

先执行步骤1，并给出检测系统未加入待测信号时，最大Lyapunov指数和内置周期驱动力幅值f的关系，如图5，其中，f为归一化值。

由图5可知，内置周期驱动力角频率为1.000 911 rad/s时所对应的fd=0.773，角频率为2.000 566 rad/s时所对应的fd=0.747 1，角频率为3.998 619 rad/s时所对应的fd=0.701。

然后执行步骤2—4，最后求出当待测信号为s1(t)时所对应的f1=0.765 896 5，f2=0.780 038 7；为s2(t)时所对应的f1=0.729 712，f2=0.764 353；为s3(t)时所对应的f1=0.674 66，f2=0.724 66。再结合步骤1的结果，代入(9)式经计算得到待测信号s1(t)，s2(t)和s3(t)的幅度，与采用直接观察法得到的幅度估计值进行对比，结果如表3。对初相位的计算结果如表4。

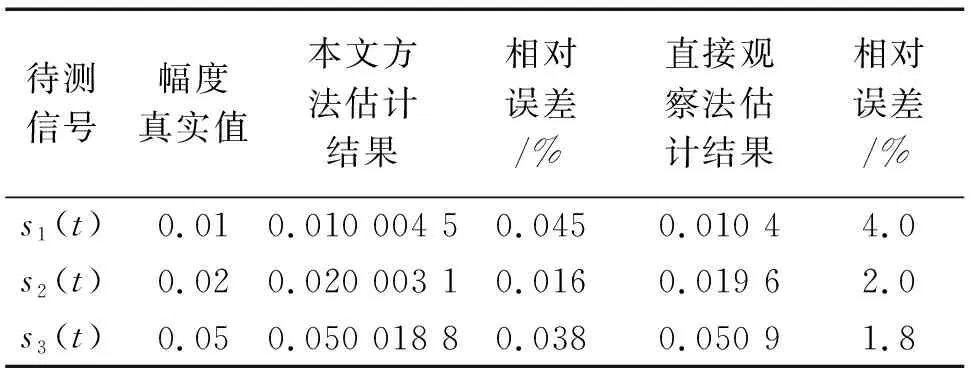
表3 2种方法幅度估计结果Tab.3 Two methods of amplitude estimation results

由表3可看出，本文方法和直接观察法相比，对待测信号幅度的估计误差更小，相对误差仅为10-4。

由表4可看出，本文方法对待测信号初相位的估计误差很小，相对误差仅为10-3。

表4 相位估计结果Tab.4 Phase estimation results

4 结 论

单一Duffing振子仅能检测与内置周期驱动力频率十分接近的微弱信号，本文从这个问题出发，提出频谱式Duffing振子方法，该方法能够只用单个Duffing振子实现未知频率信号的有效检测和频率估计，且精度可以达到10-3；在完成频率估计的基础上，还给出微弱信号幅度和初相位的估计方法，同时为避免直接观察法的主观性、效率低和Melnikov方法的精度低等缺点，采用Lyapunov指数方法作为检测系统相变判据；最后进行3组仿真实验，通过对仿真数据的分析，得出所提方法在信噪比为-43.01 dB的条件下，仍能完成对未知频率且具有任意初相位的正弦信号的检测，并对3项参数具有较高的估计精度。