哈尔滨地铁环境振动噪声测试与降噪处理*

于海英，祝 达，周宝峰，徐 旋，马温喜

(1.中国地震局工程力学研究所，黑龙江 哈尔滨 150080；2.中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

0 引言

20世纪初，Omori(1908)首次使用测震仪器观测地脉动；Kanai等(1954)在20世纪50年代将1 s以下短周期的地脉动观测值作为评估工程场地动力性能的一种方法；Udwadia和Trifunac(1973)通过对美国加州同一场地获得的地脉动与EL Centro地震波进行比较，发现两者没有相关性，并且地脉动在不同的时段亦不稳定；Thompson(2013)认为，与空气噪声类似，不同类型的在轨列车(如地面上和地下隧道内高速运行的列车)引起的振动通过大地传播后，同样会成为附近居民区的重要噪声干扰源，地面振动问题变得日益重要。地下隧道内高速运行的列车引起的振动会传递到上方地面及其周边建筑物，与地面上运行的列车引起的振动相比，其振动具有高频成分(30～250 Hz)。因此，感官上，此类振动噪声会比其它振动噪声更令人烦躁，该现象被称为“地面诱导结构声”。瑞士学者证实该现象的确存在，日本学者对日本新干线的调查结果亦有相似结论(Muller，2008；Yokoshima，Tamura，1999)。20世纪80年代以后，随着我国地震观测技术的不断进步，地脉动观测方法得到广泛应用。彭远黔等(2000)将地脉动卓越周期作为场地类型分类的标准，并给出各种场地土类型所对应的卓越周期。综上所述，国内外学者的研究主要集中在利用地脉动观测值评估工程场地动力性能、铁路环境振动噪声对列车运行线路附近居民的干扰程度，以及如何建立环境振动噪声的评价标准和制定噪声减缓措施等方面。然而，在城市地铁地震紧急处置领域，鲜有针对环境振动噪声对地震紧急处置系统中地震信号识别的影响方面的研究。事实上，在城市地铁采取地震紧急处置时，地震P波预警的效果受实时采集到的地震波的信噪比影响很大，且在P波触发后3 s内的加速度幅值与地铁环境振动噪声(尤其是在轨运行的列车引起的振动噪声)混叠在一起，使得地震P波更难被有效识别。

为了研究地铁环境振动噪声对未来城市地铁地震警报系统中地震信号识别的影响，并分析处理地铁环境振动噪声对地震信号识别的影响，针对修建城市地铁所常见的Ⅱ类和Ⅲ类场地，本文选取哈尔滨地铁1号线的4个地铁站的上行线首部和尾部作为环境振动观测点，采集凌晨安静时段和白昼列车工作时段的地脉动数据以及环境振动噪声数据。基于滑动平均法，提出确定帕曾窗带宽b值的经验方法，对所采集的数据进行分析处理，给出地脉动和地铁列车振动的加速度均方根值统计结果以及相应的频谱，并确定哈尔滨地铁地震P波预警滤波频带范围。

1 地铁环境振动观测

1.1 测试仪器

为了满足哈尔滨市地铁环境振动噪声测试的频率要求，即既要保留地脉动信号(地脉动成分在20 Hz以下的频率段内，长周期地脉动信号的频率甚至低于0.1 Hz)，也要监测到外界振动干扰信号(列车振动成分高于30 Hz)，因此要求测试仪器采样频段的下限要低于所获取信号的频段下限(曾立峰，2012)。在哈尔滨地铁的地脉动信号测量中，测试仪器主要包括2套强震动记录器和加速度传感器，分别采用美国凯尼公司(Kinemetrics Inc.)生产的Basalt型号和FBA ES-T型号。加速度传感器的频率响应范围为0～100 Hz，完全可以满足测试的频率要求。

1.2 测点布设

薄景山(2003)指出，在哈尔滨市地铁1号线(一期)18个车站中，太平桥站、交通学院站、桦树街站和哈尔滨东站所在场地为Ⅱ类场地，其它车站所在场地均为Ⅲ类场地。考虑哈尔滨市地铁环境振动噪声测试观测点应保证包括两种场地类别的车站，因此选取博物馆站、和兴路站、理工大学站和桦树街站作为测试车站。测试车站的场地参数见表1。

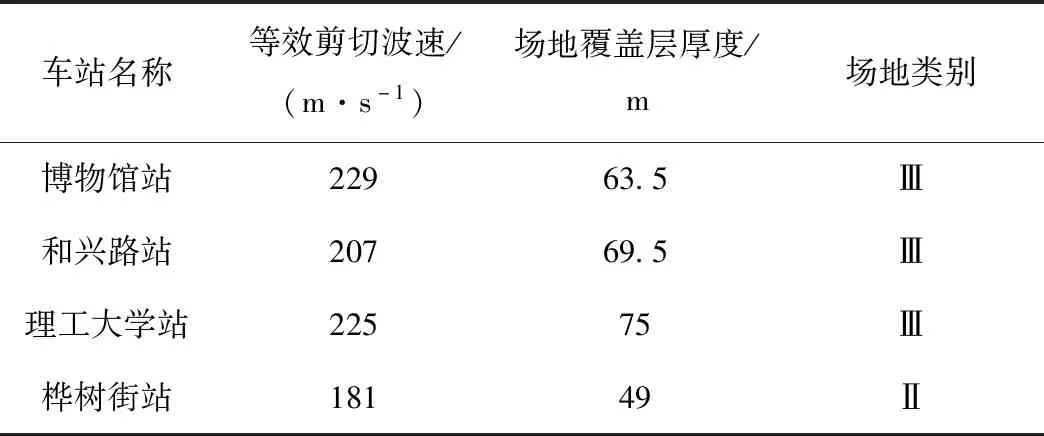
表1 测试车站的场地等效剪切波速、覆盖层厚度和场地类别Tab.1 Site equivalent shear wave velocity，cover thickness and site class of the testing station

由图1可见，加速度传感器LEA和LSA分别布设在各测试车站地铁隧道底部上行线的首部和尾部，各观测点加速度传感器与轨道间的距离见表2。加速度传感器的X轴与地铁上行线(径向)同方向，Y轴与地铁上行线(切向)同方向，Z轴为竖向。

表2 各观测点传感器与地铁轨道的距离Tab.2 The distance between sensors and tracks at all observing sites 单位：m

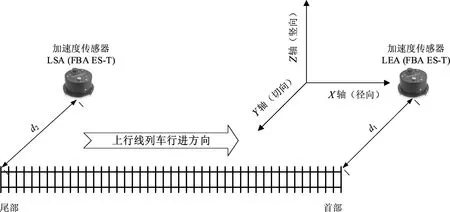
图1 环境振动噪声观测点测试仪器布置示意
Fig.1 Diagram of arrangement of testing instruments at observing sites of environmental noises

2 噪声分析

城市地铁环境振动噪声包括地铁列车振动、地脉动以及市电等产生的干扰。本文分析地铁环境振动中地脉动和列车振动噪声，仅考虑LEA和LSA所获取的加速度波形信号。从连续多天各时段观测采集的数据中提取。虽然是在凌晨进行地脉动信号的测量，但结果仍然受到地面行驶车辆等因素的干扰。干扰信号与地脉动信号相比有明显的区别：干扰信号的振动过程较短，而地脉动信号则会一直存在。这是由于地脉动信号的最大幅值不能代表地脉动的振动幅值，而是代表干扰信号的振幅(李友鹏，邹桂高，2004)。本文利用从各测试车站采集的各时段地脉动数据计算加速度均方根平均值(表3)，结果表明：各测试车站洞体的地脉动加速度均方根平均值为(3.7～8.5)×10-2gal。

表3 各测试车站地脉动加速度均方根平均值Tab.3 Average MSR of ground pulsation acceleration at all testing stations 单位：gal

从采集的各时段地脉动数据中提取加速度均方根平均值最小的、记录长度为1 min的地脉动信号作为典型，并绘制其时程曲线(图2)。从采集的各时段列车振动数据中提取典型的列车振动信号，并绘制其时程曲线(图3)。

(a)上行线首部

(b)上行线尾部

(a)上行线首部

(b)上行线尾部

由各测试车站采集的列车振动数据计算得到列车振动信号峰值加速度平均值由表4可见：与水平向振动相比，各测试车站列车的竖向振动较大；在水平向振动中，轨道切向振动大于径向振动，且水平向合成值为2.1～18.0 gal。

表4 各测试车站列车振动峰值加速度平均值Tab.4 Average peak acceleration of train vibration at all testing stations 单位：gal

根据以上分析，结合地震P波双参数阈值高铁Ⅰ级地震警报预测方法(宋晋东等，2018)，选取地震P波触发后3 s内的速度幅值大于0.05 m/s(相当于加速度幅值2.5 m/s-2)作为信噪比的评价标准对数据进行筛选。警报参数τc的计算结果受地震信号的信噪比影响较大，计算时应选取满足一定信噪比要求的地震信号。虽然地铁地脉动信号的加速度均方根平均值远远小于地震警报系统对地震信号信噪比的要求，但是地铁列车振动信号的加速度幅值(即便采用水平向合成值)与地震P波触发后3 s内的加速度幅值几乎处在同一数量级，若不对其进行降噪处理则无法有效识别地震波。

3 降噪处理

为了使城市地铁地震警报系统在地震发生时能够准确捡拾地震动信息，必须采用滤波技术有效滤除城市地铁环境振动噪声。降噪处理通常采用滑动平均法，但适用于城市地铁P波预警降噪处理的滑动谱窗的选择以及窗口带宽的确定方法尚未统一。本文基于滑动平均法，提出确定帕曾窗(Parzen Window)窗口带宽b值的经验方法。最后，利用滤波技术确定合适的滤波频带，并将列车振动及市电干扰滤除。

3.1 滑动平均法

地震动信号的傅里叶谱、功率谱会出现锯齿状起伏现象，很难确定频谱峰值的准确位置。为了解决该问题，需要对频谱做平滑化处理。基于大崎顺彦(2008)的研究，本文提出一种频谱的滑动平均法，即依次以样本点为中心点，在数据宽度为b的区间内计算中心点的平均值，并将其作为样本点的值(图4)。

图4 滑动平均法示意Fig.4 Diagram of the moving average method

经滑动平均法处理后，列车振动信号频谱的主要频率成分被凸显出来，且该方法能对从测试车站采集的海量列车振动数据进行批量地频谱平滑化处理。

在利用卷积运算对频谱进行平滑化处理时，本文只对功率谱进行平滑化，以保证不改变原频谱的功率。

(1)

3.2 确定帕曾窗带宽b值的经验方法

为保证功率谱平滑后的面积不变，且对某个中心点取值时，能够使中心点两侧数值的处理保持均衡，W(f)需满足以下条件：

(2)

满足式(2)的谱窗W(f)有多种，本文采用帕曾窗(图5)作为谱窗，即

(3)

式中：u称为时滞域上的截断宽度，一般将u当作单纯的常数处理，单位为s(大崎顺彦，2008)。

帕曾窗的带宽b为：

(4)

确定帕曾窗的带宽b值是检验滑动平均法频谱平滑化效果的关键参数。若b值过小，则经平滑化处理的频谱锯齿状现象仍十分明显，难以分辨出主频；若b值过大，经平滑化处理的频谱将过于平缓，导致主频的位置更不明显甚至削去主频。以博物馆站的地脉动信号的傅里叶谱为例，分别选取不同的b值，检验滑动平均法频谱平滑化效果(图6)。结果表明：带宽b值较小或较大均不合适；当带宽b值取0.4 Hz时，平滑化后的频谱能较好地反映地脉动信号的频谱主频。经测试，其它测试车站地脉动信号的频谱亦显示同样的平滑化效果。

图5 帕曾窗示意Fig.5 Diagram of the Parzen Window

(a)上行线首部

(b)上行线尾部

3.3 地脉动及市电干扰

首先，计算各测试车站三轴向地脉动信号的傅里叶谱和功率谱；其次，采用滑动平均法对功率谱进行平滑化处理；然后，由经平滑化处理的功率谱计算傅里叶谱；最后，由水平向(径向和切向)的傅里叶谱计算水平合成向的傅里叶谱。

水平合成向傅里叶谱fh的计算公式为：

(5)

式中：fx和fy分别表示径向和切向的傅里叶谱。

各测试车站未滤波的地脉动信号的傅里叶谱如图7所示，由图可见，各测试车站上行线首部和尾部测点的频率主要集中在2.8～50 Hz，且频率在50 Hz处尤为明显，该频率成分属于市电干扰。市电干扰主要是各观测点周围存在大量电气设备，并且测量时由于测试仪器没有接地条件造成的。为了消除市电干扰造成的影响，本文采用巴特沃斯低通滤波器(高频截止频率为10 Hz)。

(a)上行线首部 (b)上行线尾部

图7 各测试车站未滤波的地脉动傅里叶谱
Fig.7 Unfiltered Fourier spectrum of ground pulsation at all testing stations

Kanai等(1954)认为地脉动和场地土类型存在关系，可以利用地脉动观测值进行场地划分；黄蕾等(2009)则进一步认为场地土类型与地脉动的卓越周期或卓越频率存在明确的对应关系(表5)。为了探究各测试车站观测点地脉动信号的卓越频率与场地土类型之间的相关性，本文分析各测点滤波后的地脉动信号傅里叶谱。而建设部综合勘察研究院(1995)认为，地脉动信号各轴向的卓越周期不同时，应以水平向的卓越周期为主，必要时可分别提出水平向和竖向的卓越周期。因此，本文分别绘制各测点滤波后的地脉动信号竖向和水平合成向的傅里叶谱(图8)，并统计各测点相应的卓越频率(表6)。

表5 按卓越周期或卓越频率划分场地土类型Tab.5 Site soil types categorized by predominant period or predominant frequency

(a)上行线首部

(b)上行线尾部

表6 各测点的卓越频率Tab.6 Predominant frequency at all stations

结合表5、表6可知：水平向卓越频率中，只有桦树街站上行线尾部的观测点不满足场地土类型的要求；而在竖向卓越频率中，桦树街站观测点则完全不满足场地土类型的要求。综上所述，水平向卓越频率和场地土类型的相关性较好，而竖向卓越频率的误差较大。因此，巴特沃斯带通滤波器的高频截止频率选择10 Hz是比较合理的。

3.4 列车振动干扰

为了从地震动信号中有效滤除列车振动干扰，需要对列车振动信号进行傅里叶谱分析，以获得地铁列车振动信号的主要频率成分。

各测试车站观测点采集的地铁列车振动信号的傅里叶谱(图9)表明：各测试车站观测点的上行线首部和尾部的列车振动信号的频率成分均集中在30～90 Hz。由于测试专用的加速度传感器频率响应范围为0～100 Hz，因此本文引言中所提及的“欧洲地铁列车振动噪声具有高频成分(30～250 Hz)”亦得到印证。

(a)上行线首部

(b)上行线尾部

由图9可知，列车振动信号同样存在低频成分，故仍需找出地铁列车振动信号的低频成分所在范围。虽然地铁列车振动信号的低频部分的谱幅值较高，但其频带较窄。徐旋(2018)对大量地震动信号的低频截止频率进行统计分析，发现地震动的低频截止频率主要集中在0.3 Hz附近。因此，巴特沃斯带通滤波器的低频截止频率选择0.3 Hz是比较合理的。

3.5 噪声处理效果比较

为了满足地铁地震警报系统对准确性的要求，需要从各种环境振动噪声中有效提取地震动信号。环境振动噪声主要包括地铁电气设备工作引起的50 Hz市电干扰和列车振动噪声。地震动信号的频率主要集中在10 Hz以下，且列车振动信号的高频成分大于10 Hz，因此，环境振动噪声的高频成分可以较为容易地从地震动信号中被滤除。

日本新干线地震预警采用的是两个级联滤波器，滤波频带为0.05～5 Hz，由于此种滤波器设计难度比较大，因此实际采用0.075～5 Hz的4阶带通滤波器(宋晋东，2013)。在计算仪器地震烈度时，日本气象厅所使用的幅值滤波器的滤波频带为0.5～10 Hz(张红才，2013)。为了尽可能滤除地震动信号中属于地铁环境振动噪声(列车振动以及市电干扰)，本文分别选择0.3 Hz和10 Hz作为巴特沃斯带通滤波器的低频和高频截止频率。日本气象厅仪器烈度、日本新干线地震预警以及本文所采用的滤波器的频率响应如图10所示。

综上所述，本节首先基于频谱滑动平均法计算确定各测试车站地脉动信号和列车振动信号的频谱滤波频带范围为0.3～10 Hz，然后采用巴特沃斯带通滤波器滤除地震动信号中环境振动噪声，最后计算得到各测试车站经滤波处理后的列车振动信号的峰值加速度均方根平均值(表7)。

图10 滤波器频率响应示意Fig.10 Diagram of filter frequency response

表7 各测试车站滤波后的列车振动的峰值加速度均方根平均值Tab.7 Average MSR peak acceleration of filtered train vibration at all testing stations 单位：gal

对比表3和表7可知，经滤波处理后的列车振动(3.8～7.6)×10-2gal与地脉动信号的峰值加速度均方根平均值(3.7～8.5)×10-2gal处于相同数量级，且被包含在地脉动信号的峰值加速度均方根平均值区间内。

考虑博物馆站观测点列车振动信号的滤波前后效果，从图11可以看出：经过滤波处理后，市电干扰以及列车振动干扰均被滤除。因此，本文确定的巴特沃斯带通滤波器的滤波频带(0.3～10 Hz)是合理的，其对哈尔滨地铁环境振动噪声的滤波处理效果是明显的。

(a)上行线首部 (b)上行线尾部

图11 博物馆站观测点列车振动滤波前后的时程曲线
Fig.11 Time-series curves of filtered and unfiltered train vibration at the Museum Station

经过以上降噪处理后，地铁地脉动信号和列车振动信号的峰值加速度均方根平均值远远小于地震警报系统对地震信号信噪比的要求，可更容易识别出地震P波信号。

4 结论

本文以哈尔滨地铁1号线包含Ⅱ类和Ⅲ类2种场地土类型的4个地铁站的上行线首部和尾部作为观测点，展开地铁环境振动噪声的测试、分析以及降噪处理研究，得出以下结论：

(1)各测试车站观测点洞体的地脉动信号的加速度均方根平均值在(3.7～8.5)×10-2gal。三轴向地铁列车振动信号中，与水平向振动相比，各测试车站列车的竖向振动较大；在水平向振动中，轨道切向振动较大于径向振动，且水平向合成值在2.1～18.0 gal。

(2)各测试车站观测点凌晨安静时段的地脉动信号受地铁环境工作的电气设备引起的频率为50 Hz的市电干扰的影响较大。经高频截止频率为10 Hz的巴特沃斯低通滤波器进行滤波处理后的地脉动信号的卓越频率和场地土类型有明显的对应关系，即：水平向卓越频率和场地土类型的相关性较好，而竖向卓越频率的误差较大。

(3)基于滑动平均法的经验方法确定帕曾窗带宽b值为0.4 Hz，平滑化后的频谱能较好地反映地脉动信号的频谱主频。确定各测试车站地脉动信号和列车振动信号的频谱滤波频带为0.3～10 Hz时，能较好地滤除地脉动信号中地铁环境振动噪声(列车振动以及市电干扰)的频率成分。并与日本气象厅仪器地震烈度以及新干线地震预警系统的滤波频带进行对比。经过该频带滤波处理后的列车振动信号与地脉动信号的峰值加速度均方根平均值处于同一数量级上，且被包含在地脉动信号的峰值加速度均方根平均值区间内，而且远远小于地震警报系统对地震信号信噪比的要求。

本文所得到的从各测试车站观测点采集的凌晨安静时段的地脉动数据以及列车工作时段的过车振动数据的分析结果可为今后城市地铁紧急处置技术研究提供参考依据，测试数据本身亦可为今后城市地铁的地震安全性评价和设计提供极具价值的科学数据支撑。

本课题组在对哈尔滨地铁1号线进行环境振动噪声测试的过程中得到了哈尔滨地铁集团有限公司的宝贵支持与配合，在此表示衷心感谢！