非价格数据中的价格信息——对中国价格指数的动态分析

贾卢魁

（中国人民银行 清算总中心，北京100800）

一、引言

在宏观经济研究中，对各种价格指数的分析始终处于核心位置。从理论上看，价格指数的动态变化反映了市场的出清情况；在实践中，价格的波动直接影响了私人部门和公共部门特别是中央银行的经济行为和决策。在众多价格指数中，最受关注也是最为重要的就是消费者价格指数（Consumer PriceIndex，CPI）。这一综合价格指标不但与社会经济活动息息相关，同时还被政策制定者视为反映实体经济运行状态和市场出清情况的重要指标。

基于CPI 的重要性，众多研究人员进行了大量相关研究，并取得了丰硕的成果。但是，传统结构模型分析方法的一个主要挑战在于无法在一个统一自洽的模型框架中将时效性（Timeliness）和准确性（Accuracy）同时实现，特别是在输入数据的维度很高时。这就是典型的“维度咒诅”（Curse of Dimensionality）问题：当输入变量数量增多时，模型所需要刻画的各变量间的结构关系急剧上升，对应模型中的参数个数也快速增加。这就使得当模型使用的输入变量数量众多时，模型识别（Model Identification）将变得十分困难，甚至基本是不可能的。即使在某些特殊情况下可以求得所有参数的估计值，模型的稳定性也根本无法保证。由于现代社会中经济体内各参与者的经济活动频度更高也更加复杂，为了得到精确的宏观经济分析结果，需要从众多的数据指标中获取尽可能多的有效信息。因此，“维度咒诅”问题在宏观经济分析中显得尤为突出。

针对理论和实证分析中遇到的挑战，已经有很多宏观经济研究人员将目光投向了降维（Dimensionality Reduction）分析中的主成分分析（Principal-Component Analysis，PCA）方法，使用该方法将大量数据指标中隐含的、不可观测的共同动态因子信息提取出来用以描述经济体的宏观指标（主要是GDP增长率和通货膨胀率等）的趋势性变动。这种方法在机器学习、模式识别和气象预测领域被广泛使用，并取得了巨大成功，有效解决了“维度咒诅”问题，实现了高维数据的自洽动态模型。本研究也将理论框架和实证分析模型建立在主成分分析和动态因子模型（Dynamic Factor Model，DFM）之上。与之前的研究不同，在本文中，我们试图从非价格指标中提取动态共同因子用以研究价格指标的动态特征。这些非价格指标表征了经济体中各个部门的运行状态，因此通过本研究可以从一个全新的角度进一步分析价格指标与经济活动的动态关系。本研究的另一个主要贡献在于建立了一个完整的基于监督学习（Supervised Learning）的动态跟踪和实时预测（Nowcasting）平台，该平台可以根据输入数据的不断更新实现对价格指标的实时预测。

本文的结构如下：在简介之后，第二部分主要总结了本文的研究背景和对主要的相关文献进行了综述；第三部分重点讨论了本文使用的研究方法，即基于主成分分析的动态因子模型；第四部分详细介绍了实证分析阶段使用的数据信息集合以及实证研究结果；第五部分给出了对本研究的总结与讨论。

二、文献综述和研究背景

在几乎所有现代宏观经济分析中，对价格的研究始终处于重要的核心位置，对于货币政策制定者而言尤其如此。随着经济和金融市场的发展，货币当局需要什么样的政策框架是一个不断演化的课题，在不同时期不同历史背景下有着不同的侧重。从20 世纪80 年代以来，通胀定标（Inflation Targeting，IT）逐渐被越来越多的经济体采用。各主要经济体的央行在制定货币政策过程中都将价格水平纳入政策制定和评估模型中，其中的代表就是基于新主流宏观经济学（New Consensus Macroeconomics，NCM①在学界，关于现代主流宏观经济学还存有一定的争论。有一大批学者将其称为新凯恩斯经济学（New Keynesian Economics，NKE），因为其包含了凯恩斯经济学关于价格黏性的特征；另一些学者则将其称为NNS(New Neoclassical Synthesis)以体现其对新古典经济学的发展和融合。这里，我们使用NCM 这一更加宽泛的概念，以体现这一框架同时继承了凯恩斯经济学与古典经济学的重要属性。或者New Wicksellian Macroeconomics, NWM）框架②关于现代主流宏观经济学的更具体内容尤其是NCM 理论框架，可以参见Goodfriend、King（1997）[1]以及Arestis（2009）[2]的研究。的动态随机一般均衡（Dynamic Stochastic General Equilibrium，DSGE）模型。通货膨胀在这种通胀定标的货币政策框架下得到了较好的控制③学术界对于通胀定标的货币政策及其效果仍然存在争论，例如Arestis（2006）[3]就认为低通胀并非因为央行实施通胀定标政策；Cecchetti（2000）[4]批判了央行单一关注通货膨胀率的货币政策而忽略资产价格的政策框架，指出央行在制定和执行货币政策时还应该考虑通货膨胀率之外的其他因素。：从20世纪90年代开始，西方主要经济体的通货膨胀处于比较低的相对稳定水平，凸显了中央银行对价格指数动态特征研究的重要性。

前期的成果包括基于回归算法并使用各种价格指数和金融经济变量（包括资产价格、货币发行量增速、信贷扩张率）作为研究整体通胀水平的指标（Inflation Indicators）。具有代表性的研究包括Engle（1982）[5]使用ARCH 向量自回归模型对英国通货膨胀走势的动态特性进行研究，取得了重要成果；Blundell-Wignall 等（1990）[6]基于通货膨胀的自身惯性（Inflation Inertia），提出通胀具有强顺周期性且对货币政策变化以及实体经济冲击的反应体现出明显的滞后性（6 个季度）。这是由于外生冲击对经济体的影响首先体现在经济活动中，然后才会影响到整体价格水平。因此，表征这些经济活动情况的指标可以作为研究通货膨胀未来变动趋势的先行指标（Leading Indicator）。基于以上分析，Blundell-Wignall 等（1990）将利率变动对通胀影响的先行指标分为三类：汇率、信贷、资产价格。Cecchetti（1995）[7]在通胀定标框架下分析了货币政策传导机制以及相应的通货膨胀先行指标，得到了与之前相似的结果，即通胀对外生冲击的反应有较长的时滞。因此，可以通过对经济变量的变化预测通货膨胀的未来走势。但是，由于经济变量与通胀之间关系会随时间发生变化，所以这项工作极具挑战性。

还有一批学者试图从微观层面研究整体价格水平的动态特征。例如，Caballero 和Engel（1993）[8]基于微观主体价格调整的行为特征构建模型研究了二战后美国的整体价格波动；Perazzo 等（1997）[9]也建立了相似的动态模型研究厂商调整价格和产量的行为对整体价格水平的影响。Gupta（2017）[10]比较了基于经济学理论基础的模型（DSGE Models）和基于统计回归分析（Non-structural Models，主要是向量自回归模型）的模型在预测通胀走势方面的差异，得到了这样的结论：在预测短期走势方面，非结构模型具有优势；而在长期通胀水平的估计方面，基于经济学理论的模型表现更好。相似的结果可以在Gupta 等（2011）[11]对美国房地产市场价格的分析中得到。总之，预测和分析通货膨胀水平的未来变化对中央银行具有重要的意义，同时也是一项艰巨而复杂的任务。

本文使用基于主成分分析的动态因子模型PCA/DFM 对高维度时间序列进行动态分析，从中提取隐含的反映实体经济运行情况的动态因子。与之前的研究不同，我们试图从直接反映实体经济运行状态的非价格指标数据集合中提取共同因子。通过计算这些动态因子与价格指标的动态联系，可以得到如何从非价格指标中解读价格指标的动态特征，进而解读外生冲击如何通过影响具体的经济活动并最终传导至价格水平。此外，本文引入监督学习下的自动化方法，构建价格总水平实时预测分析平台，为政策分析、制定与执行提供有效的参考信息。

三、研究方法

（一）主成分分析

计量分析中一个关键的挑战在于模型的参数识别问题：为了获得更精确的分析结果，往往需要尽可能多地考虑相关的变量，但是随着变量的增多，模型所需要估计的参数数量快速增加，模型的稳定性和可识别性都急剧下降。这一问题被称为“维度咒诅”。随着信息技术和人工智能的发展，特别是降维分析算法的成熟，研究人员具备了从高维度信息中提取隐含的决定性共同因子（Salient Common Factors），并以此获得经济体运行的趋势性信息。在众多降维分析算法中，被广泛使用的是主成分分析（Principal Component Analysis，PCA）方法。这一方法在机器学习领域和高维度分析领域取得了丰富的研究成果。

在本研究中，我们构建了基于主成分分析的动态因子模型（PCA/DFM），在降维分析的同时有效提取高维度经济变量中隐含的宏观趋势变动因子，并以此作为研究整体价格水平动态特征的基础。假定模型的输入数据为XT×N∶xt,i，t=1,2,…,T，i=1,2,…,N，即N 个变量在T 个时期的面板数据集合。首先将输入变量变换为去均值离差的形式，则MN×N(XT×N)为样本相关矩阵，即

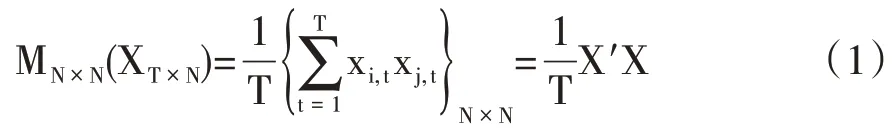
PCA 降维算法等价于寻找到一个从N 维空间到P 维空间的最优降维映射从数学角度讲，建立这种最优映射即在N 维空间中寻找一组归一化正交基使得原数据在这v→1上的投影长度最大，在上的投影长度次之，以此类推寻找到的前P个基第一步是求解向量v→1，即：

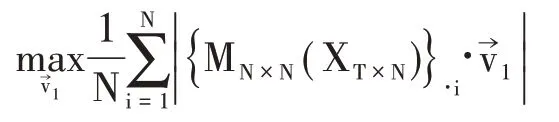
这就等价于①算符{ }·i 和{} j·分别返回括号中矩阵的第i行和第j列。：

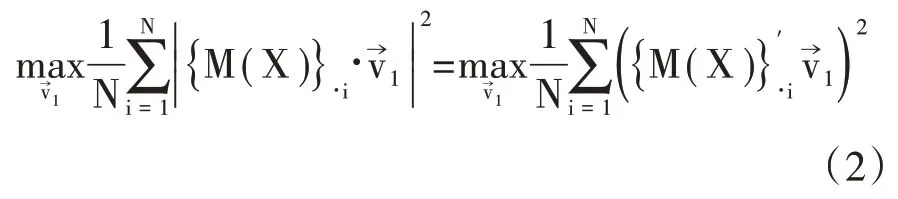
且

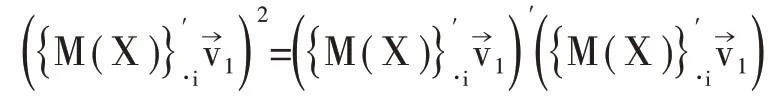
结合式（1），可以将式（2）转化为：

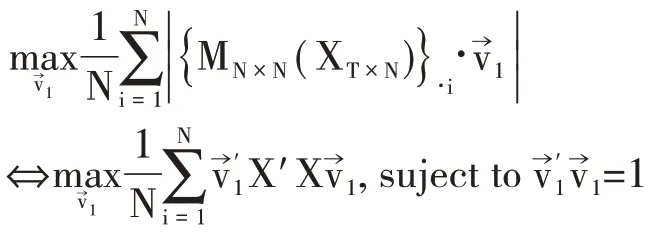
对应的拉格朗日方程为：

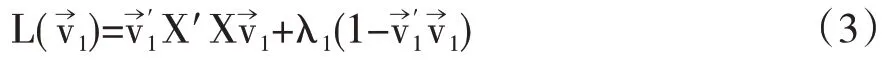
对式（3）求导可得一阶条件为：

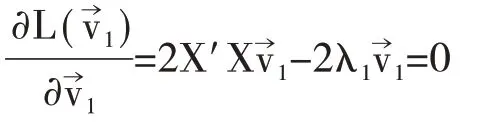
式（4）说明，满足式（2）的向量v→1即为样本相关矩阵X′X 最大特征值λ1所对应的特征向量。因此，求解PCA 最优降维映射的过程等价于求解样本相关矩阵的所有特征值及特征向量的过程，并按照特征值从大到小的顺序排列，选取前P 个特征值和对应的特征向量，即可求得样本所包含的主成分。由于样本相关矩阵MN×N(XT×N)是实对称矩阵，因此一定可以将其分解为特征向量矩阵VN×N和特征值对角矩阵的形式：

将式（4）和式（5）合并可得：

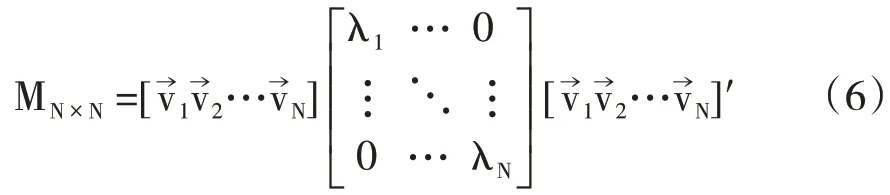
其中对角矩阵按照λ1至λN从大到小的顺序排列。这样，就可以使用PCA 最优降维映射求得样本中蕴含的主成分̂T×P为：

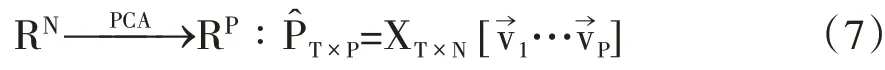
从PCA 算法可见，每个主成分对解释样本相关性的贡献程度正比于该主成分对应的特征值。我们进而定义前P 个主成分的累计解释贡献度（Accumulated Explaining Power,AEPP）：

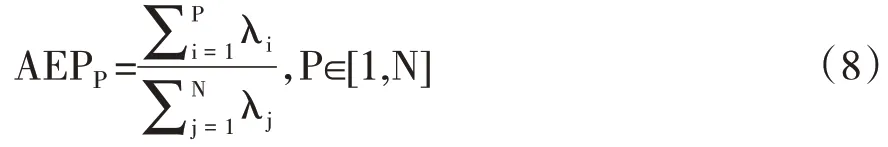
易见，AEPP≤1且等号只在P=N时成立。

（二）动态因子模型

在数据降维提取公共因子之后，通过构建这些公共因子的动态特性，就可以得到动态因子模型。本研究采用Giannone 等（2008）[12]、Bok 等（2018）[13]以 及Yiu 和Chow（2010）[14]提 出的框 架建设 模型PCA/DFM。PCA 分析得到的样本隐含的主成分序列P̂T×P可以使用状态空间表示为,t∈[1,T]，且进一步假定该状态空间时间序列满足一阶自回归AR(1)过程：

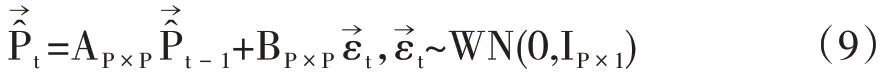
其中AP×P为P维状态转换矩阵。

使用最小二乘法对式（9）进行拟合计算可以得到状态转换矩阵的样本估计值：

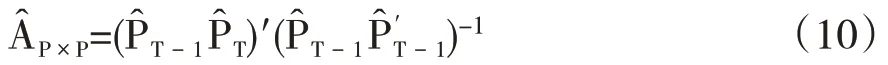
其中：

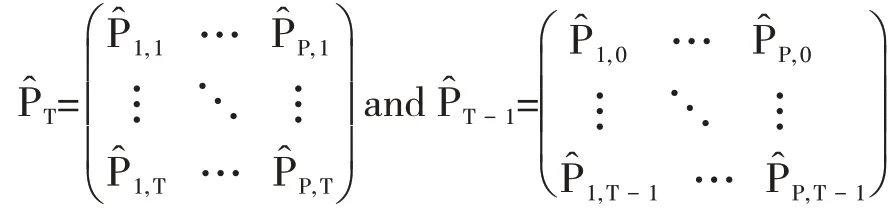
使用状态空间对主成分动态因子进行描述的一个重要便利性在于，可以使用Kalman 滤波对样本内涵主成分序列进行动态优化，得到最优的样本主成分时间序列

PCA/DFM 的核心思想在于高维度数据输入中的每个时间序列都包含了系统整体趋势性运动的信息以及该变量自身对整体趋势性变动的反应。具体而言，每个变量随时间的波动变化都可以被分为两个正交的部分：第一部分是整体趋势性变动［对应式（11）中的第二部分是整体趋势性变动

在该变量空间中的扩散效应，该效应只与变量自身的属性相关［对应式（11）中的U］。因此，可以建立起样本主成分时间序列与被解释变量时间序列YT×1之间的最优映射等价于求解最大似然条件下的参数向量

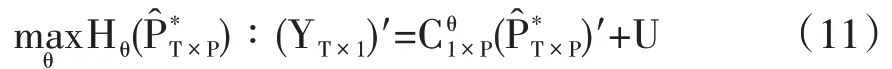
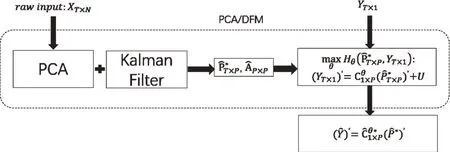
图1 包含Kalman滤波的PCA/DFM模型架构图

基于参数向量Cθ1×P（亦被称为因子载荷，Factor Loading 向量）可以得到动态因子描述的被解释变量时间序列YT×1所对应的整体趋势性变动时间序列如图1 所示，至此我们已经构建了包含Kalman滤波的PCA/DFM模型。

四、数据信息集合与实证分析

（一）数据信息集合

如前所述，包括各种外生冲击对经济体的作用首先反映在经济活动中，之后体现在通货膨胀的变动中。Giannone 等（2008）和Bok 等（2018）的研究从理论和实证方面说明，表征经济活动的每个个体指标中都包含了关于宏观经济整体运行状况的信息。因此，从高维度指标中提取共同因子可以反映宏观经济的趋势性运行状态。本研究试图从非价格指标中提取共同因子用以分析通货膨胀的动态特征，这样就避免了通货膨胀分别作为解释变量和被解释变量同时出现在方程中①正如Bok等（2018）所述，这一做法提升了模型的自洽性和一致性。。因此，需要这些非价格指标充分反映经济活动的各个方面。综合考虑数据可得性和内容充实性，我们选取了65 个经济指标时间序列②理论上，对于输入变量的维度并无限制。因此，在实践中可以根据需要灵活调整输入变量的维度。，涵盖投资、消费、生产、财政、金融等多个方面③具体而言，本文所采用数据来自国家统计局经济月度数据的官方分组，共包括除价格指数之外的11 组月度数据：工业、能源、固定资产投资（不含农户）、房地产、国内贸易、对外经济、交通运输、邮电通信、采购经理指数、财政、金融。综合考虑数据质量、数据长度、数据相关性，并参考已有的宏观实时预测分析模型［Bok等（2018）以及Yiu和Chow（2010）］所使用的数据集合，本文重点选取了这11组月度数据的65个指标作为本模型的输入。如前所述，由于FCA/DFM模型的自洽性，数据指标的选取具有很强的灵活性，可以根据实际需要灵活调整、缩减或者扩充，同时保持好的精确性和一致性。。对应的时间区间为2008 年1 月至2019 年12月，数据频率为月度，即式（1）中N=65，T=144。主要数据来源为国家统计局和CEIC数据库。

（二）实证分析结果

将数据输入图1 所描述的PCA/DFM 模型，其中65 组反映实体经济运行状况的非价格指标数据对应XT×N，同期的CPI 数据对应YT×1。实证分析的第一步是确定动态因子的数量，即式（7）中的P 值。如Yiu 和Chow（2010）以及Bai 和Ng（2002）[15]的研究所示，有多种方法可以确定模型所需的最优因子数量，很多研究直接将该值刻度为2。目前被广泛接受的判定标准是：当新增动态因子所带来的边际解释率的提升在10%左右时停止增加，即式（8）定义的AEPp+1-AEPp≤10%。

图2显示了提取的主成分因子对XT×N波动的解释度情况。前3 个主成分因子的累计解释度超过60%，这充分表明了主成分因子提取的正确性，通过提取少量的几个共同因子就可以精确描述由该维度数据描述的复杂经济系统的整体变动趋势。图2的右图显示，按照边际解释增加小于10%的标准，本模型的动态因子个数P=2。由于第3 个共同因子的边际解释贡献为8.54%，非常接近10%，而第4 个共同因子的边际解释贡献率仅为5.88%，因此我们在模型中假定P=3。

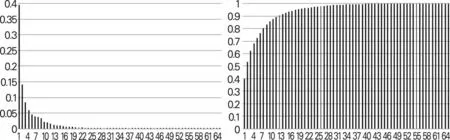
图2 单个因子的边际解释度（左图）和因子的累计解释度（右图）

在确定模型中动态因子的个数之后，使用将数据代入式（7）至式（10）所表示的PCA/DFM 模型进行实证分析，建立起从原始数据XT×N到主成分动态因子 的 映 射通 过Kalman 滤波后得到最优动态因子时间序列。进而，计算可得最优动态因子到通货膨胀水平YT×1的映射

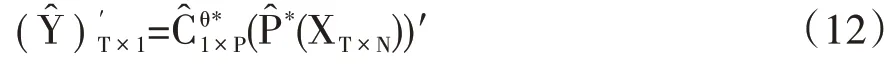
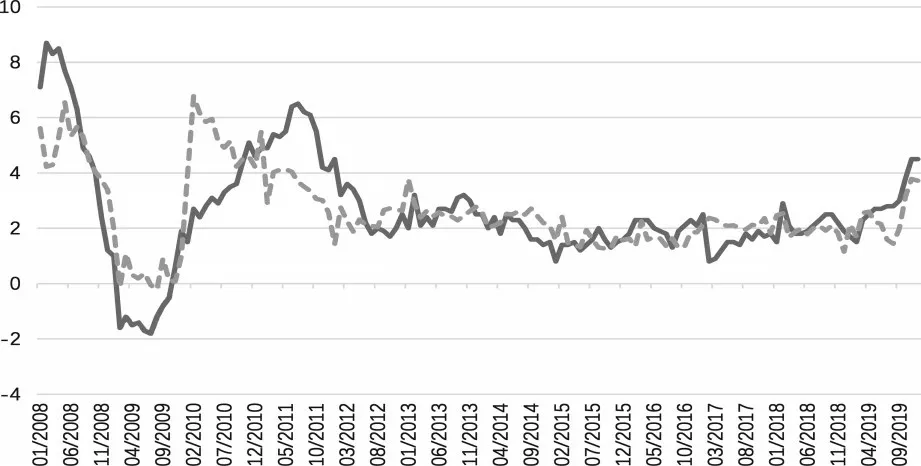
图3 通货膨胀实际观测值YT ×（1黑色，实线）与PCA/DFM模型提取的主成分动态因子所表征的通货膨胀变动趋势( ̂)（灰色，虚线）

图3 给出了通货膨胀实际观测值与PCA/DFM模型提取的主成分动态因子所表征的价格变动趋势

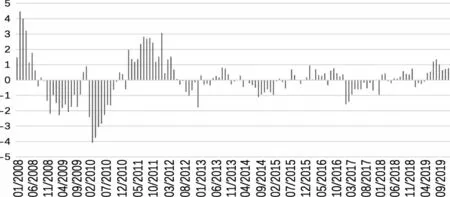
图4 通货膨胀实际观测值与PCA/DFM模型提取的主成分动态因子所表征的价格变动趋势(̂)的差

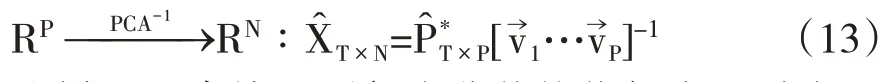
这样可以直接观测每个非价格指标变量随宏观动态因子的变化情况。图5 显示了原始的65 组输入变量时间序列和̂T×N的3D 视图。可以发现，主成分因子对各个收入指标的影响不尽相同。亦即，每个指标中包含的关于经济体整体特征的信息量与其在主成分因子向量上的投影长度成正比。因此，可以定义第i，i∈[1,N]个非价格指标与通货膨胀基础性变化的联系强度pi为相关性矩阵的第i 行在3 维基向量上的加权投影长度。

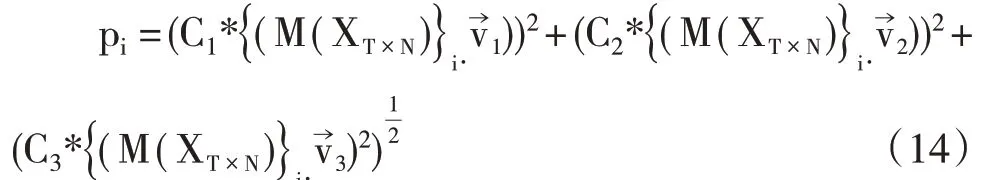
根据定义，pi的值越大对应第i个指标对通货膨胀趋势性变动的影响（联系）越显著。

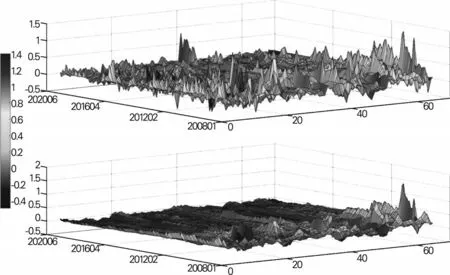
图5 原始输入变量时间序列（上图）与使用主成分重建的输入变量的趋势性变动（下图）

通过对所有65 个输入指标进行式（14）的计算，可以得到每个指标对通货膨胀趋势性变动的联系（贡献）强度。如表1 所示，我们总结了对通胀水平趋势性变动联系最为显著的15个变量。

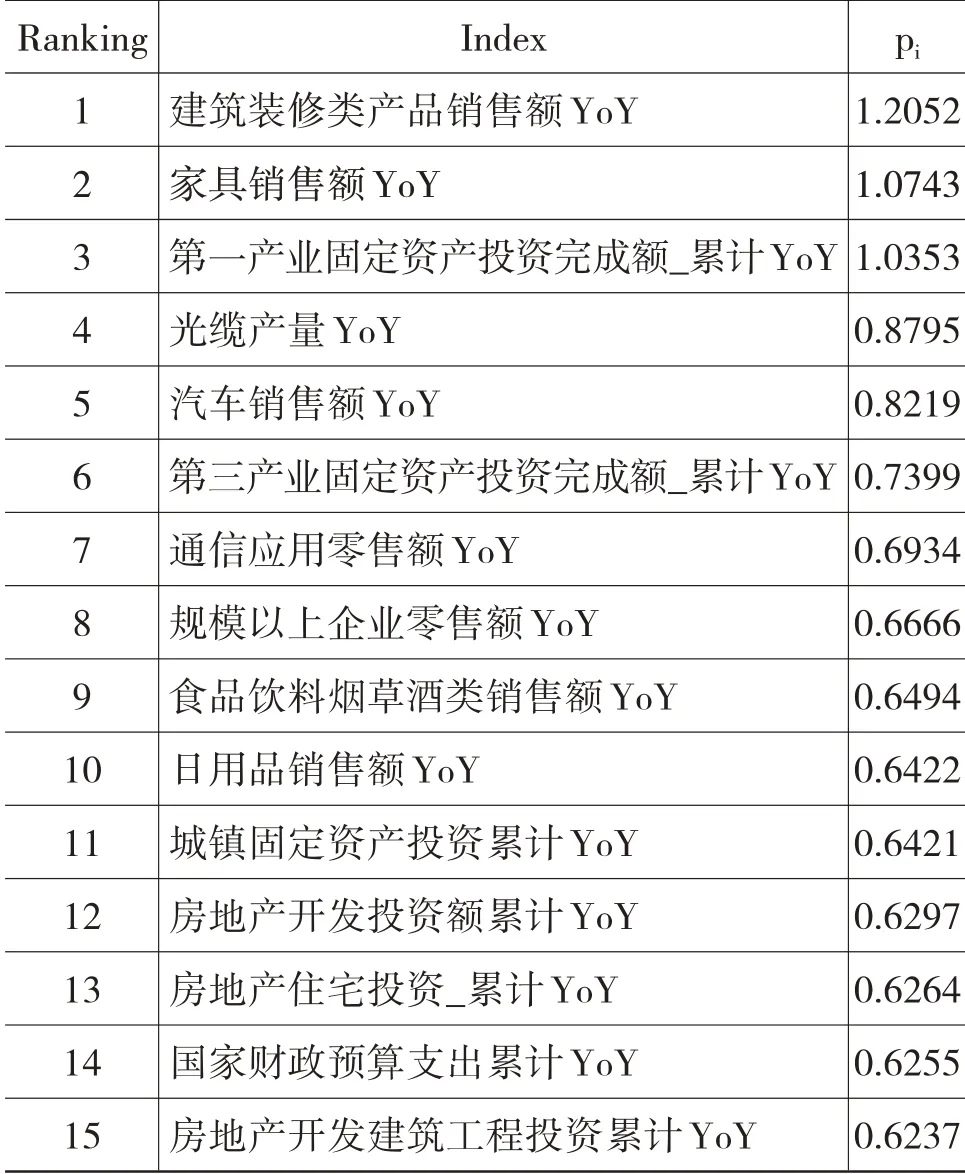
表1 输入指标与通货膨胀基础性变化的联系强度pi（前15个）

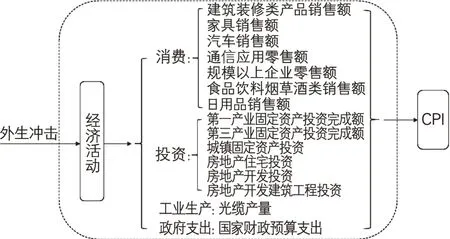
图6 实证分析得到的外生冲击对通货膨胀水平的影响机制（选取前15个关键指标）

通过对这些变量的分析可以发现，对我国通货膨胀水平的趋势性变动影响较大的经济活动主要包括各种与房地产和住房相关的指标（建筑装饰、家具以及房地产开发投资）、日用消费产品的销售额、固定资产投资额、通信及汽车销售额、政府预算支出等。图6总结了实证分析得到的外生冲击对通货膨胀水平趋势性变化的主要影响机制：外生冲击主要通过影响消费、投资、工业产出和政府支出这4 大类经济活动影响通货膨胀。通过分析这4大类15个关键指标的变动情况及其背后所代表的经济活动，可以帮助我们更好地理解经济体对外生冲击的反应机理和通货膨胀形成机制。

（三）监督学习自动化机制

为了实现对通货膨胀情况的实时分析预测，需要将PCA/DFM 动态化，这也是本文的重要贡献。基于主成分分析的动态因子模型提供了良好的自动更新动态机制，我们将监督学习引入该自动化实时分析预测机制中。如图7 所示，这是对原有由图1 表示的PCA/DFM 机制（对应黑色箭头连接的流程）的拓展，使其可以根据输入数据指标的更新计算新的通胀水平预测值（对应灰色箭头连接的流程），实现了数据驱动的动态实时分析预测。

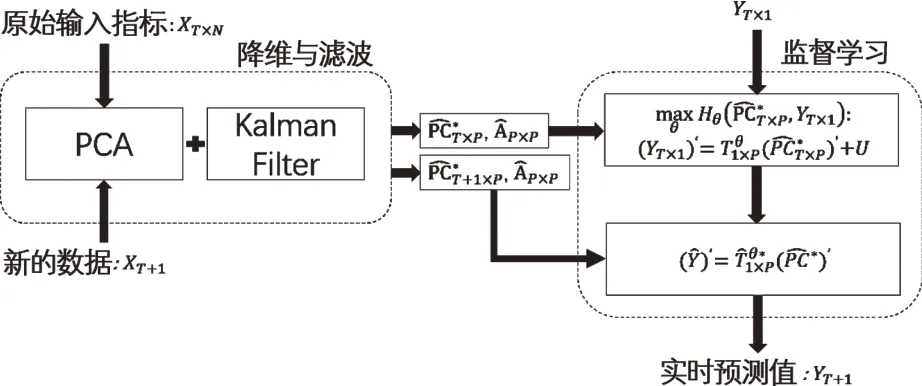
图7 基于PCA/DFM的监督学习自动化实时分析预测机制

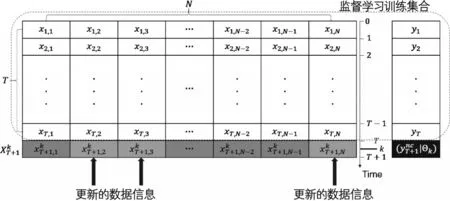
图8 输入数据更新驱动的实时分析预测

这种由输入数据更新驱动的实时分析预测机制的具体实现如图8所示。已有的XT×N和对应的YT×1构成完整的监督学习学习集，由此计算得到最优主成分因子序列最优映射参数向量以及主成分因子序列的AR(1)动态变换矩阵ÂP×P。在T 至T+1之间的k时刻（由于本研究使用的是月度数据，k可为T月末至T+1月末间的任意一天），当65个输入变量中的任何一个或几个数据更新时，将更新的观测数值代入对应的输入队列中（如图8 中灰色的位置未更新数值则使用̂P×P和

五、总结与讨论

对通货膨胀的研究在宏观经济理论和实践中都处于非常重要的位置，特别是对于各中央银行而言，更需要及时、准确的通胀预测。本文通过构建基于主成分分析的动态因子模型PCA/DFM，使用高维度（65 个）的直接反映实体经济活动的非价格指标变量集合对我国通货膨胀变化的动态特征进行了实证研究。

结果显示，外生冲击主要通过影响消费、投资、工业产出和政府支出这4 大类经济活动影响通货膨胀。其中对通货膨胀变化影响最为显著的指标是建筑装修类产品销售额、家具销售额、汽车销售额、通信应用零售额、食品饮料烟草酒类销售额、日用品销售额、第一产业固定资产投资完成额、第三产业固定资产投资完成额、城镇固定资产投资、房地产住宅投资、房地产开发投资、光缆产量和国家财政预算支出等。通过分析这4大类15个关键指标的变动情况及其背后所代表的经济活动，可以帮助我们更好地理解经济体对外生冲击的反应机理和通货膨胀形成机制。

此外，本研究将PCA/DFM 和监督学习结合起来构建了一个数据驱动的自动化实时分析预测模型，可以实现对通货膨胀变化的实时分析与预测。该模型具有很强的可移植性和拓展性，通过调整输入参数可以用于其他综合性变量的分析中。