基于双稀疏模型和非局部自相似约束的超分辨率算法研究

朱 晨,杨 欣,谢堂鑫,周大可

(南京航空航天大学 自动化学院，江苏 南京 210000)

数字图像作为网络时代信息的重要载体，其地位日益凸显.高分辨率(high resolution，HR)图像能够提供比低分辨率(low resolution，LR)图像更多的信息，在安防、医疗、探测等诸多领域HR图像具有重要的应用价值.由于环境、硬件、成本等因素制约，直接获取场景HR图像往往难以实现，为满足对HR图像的需求，我们有必要研究从LR图像恢复HR图像的方法.超分辨率(super resolution，SR)方法从早期的基于频域方法到后来的基于空域方法，逐渐发展出三类方法[5]，分别是基于插值方法[1-2]，基于重建方法[3-4]以及基于学习的方法.在基于学习的方法中，基于稀疏理论的方法由于其对图像特征的学习能力和表征能力，成为研究的热点.Yang等[9]首先提出了基于块稀疏的SR模型，Zeyde等[11]在此基础上引入K-SVD[17]字典及PCA降维，取得了效果和效率的提升.Dong等[12]通过引入图像的非局部自相似性特性以降低稀疏编码噪声，提出了非局部集中超分辨率方法.Timofte等[14-15]引入岭回归模型将重建过程放在训练阶段，提出锚定邻域回归模型(anchored neighborhood regression，ANR)及改进方法A+，大幅降低了重建时间消耗并取得效果提升.Zhang等[16]在基于稀疏表示模型中引入低秩约束，进一步恢复了重建图像的自然结构特性.国内，针对高效保持图像几何及纹理结构问题，孙宝玉等[10]提出基于多形态稀疏正则的多帧SR凸变分模型，彭真明等[13]使用多尺度字典对图像不同区域分别重建再融合，获得更好的效果.

本文针对高维信号在K-SVD字典上表示误差大，图像重建时缺少结构约束等问题，提出引入一种双稀疏字典模型[18-19]，通过结构化字典和非结构化字典结合，有效保证高维信号训练过程的进行，同时保持对样本空间表征能力.重建阶段引入图像非局部自相似性约束，约束模型解空间，使重建图像结构更接近自然图像.实验结果表明，本文算法在客观评价指标及视觉感知效果上均获得一定提升.

1 本文算法

传统的基于稀疏表示的超分辨率方法中，图像超分辨率问题可以转换为输入图像在先验过冗余字典上的最优稀疏解求解问题.设同一场景下x∈Rn表示为原始HR图像块，y∈Rm表示为降质后的LR图像块，S∈Rm×n为下采样矩阵，H∈Rn×n为模糊算子，n为加性高斯白噪声，图像的退化过程可以表示为：

y=SHx+n

(1)

超分辨率问题可以看作是求解式(1)的病态逆问题，如下所示

(2)

在基于稀疏表示的图像超分辨率方法中，我们假设输入及输出信号y，x可被稀疏表示，即x=Dhαh，y=Dlαl，Dh和Dl分别为一对协同训练的高、低分辨率过冗余字典，αh和αl分别为x和y在对应过冗余字典上的稀疏表示系数.由于字典Dh和Dl在同分布训练集上协同训练，对于稀疏表示系数有如下关系αh≈αl，因此我们可以用α指代αh和αl.结合式(2)，SR问题可以转换为最优稀疏表示系数求解问题，如式(3)所示

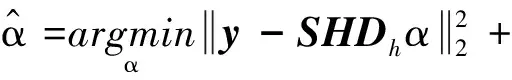
(3)

式(3)中，λ表示正则化项平衡因子，α0为L0范数约束项.由于L0范数约束会导致式(3)变成一个NP难问题，因此一般将其松弛到L1范数约束作为其最优凸近似，从而可使用凸优化方法求解，式(3)可变为

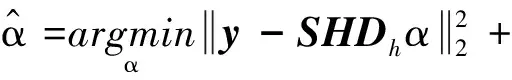
(4)

1.1 双稀疏字典模型

在字典训练阶段，我们基于已有的HR图片集{Xi}生成LR图片集{Yi}.使用双三次插值法对{Xi}作下采样和上采样，放大因子为s，生成尺寸相同但高频细节信息丢失的LR 图片集{Yi}.基于稀疏表示SR方法普遍采用K-SVD字典作为重建过程的过冗余字典[11,14-15]，训练过程通过在{Xi}和{Yi}上协同训练高低分辨率字典对保证稀疏表示系数的一致性.由于字典误差随信号维度增大而增大，上述方法通常对信号降维来减小误差，但这会导致原本信号信息丢失.考虑上述问题，我们引入文献[19]中的双稀疏字典模型：

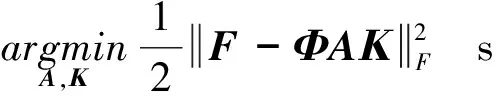
(5)

其中，F∈Rn×N表示包含N个n维向量的样本矩阵，Φ∈Rn×l表示给定的隐式结构化字典如DCT，小波字典等，我们称之为基字典，A∈Rl×m表示学习到的显式非结构化稀疏字典，Κ表示稀疏系数矩阵，q控制Κ中原子的稀疏度.

通过引入式(5)描述的双稀疏字典模型，稀疏字典可以表示结构化字典和非结构化字典的乘积，即D=ΦA，D的每一个原子为基字典Φ的有限t个原子的线性组合表示.结构化字典具有快速实现的优点，但对于复杂的图像数据缺乏自适应性，对信号的表示能力较差，非结构化字典则往往在样本空间上具有很好的适应性，但计算消耗大.通过在字典训练过程引入上述双稀疏字典模型并融合考虑结构化和非结构化字典，使得该模型在保持快速性的同时也能够有效适应样本空间，为处理更大维度的信号输入提供了有效计算条件.

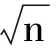
Fh≈DhK

(6)

由式(6)可计算得到Dh≈FhK+.因此，公式(4)在引入上述模型后可以写成如下形式

(7)

1.2 非局部自相似性

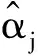
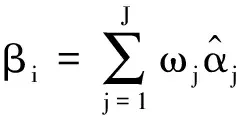
(8)

其中ωj为高斯权重系数，计算方式如下

(9)

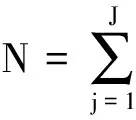
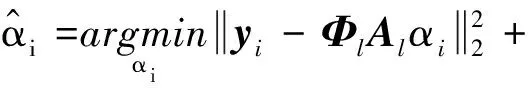
(10)

其中τ为非相似性约束项平衡因子.

1.3 整体算法

本文提出通过引入一种双稀疏字典模型作为图像SR重建的稀疏编码字典，并在重建阶段利用自然图像的非局部相似性对问题求解作进一步约束，迭代求解获得最终的SR图像.图1为本文算法流程图.

本文算法步骤如下.

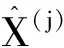
2 实验结果与分析

本文实验环境CPU为Intel Core i7-8700K，内存为 32 GB，所有实验均在Matlab2016b环境下完成.为验证本文算法有效性，设置对比方法为Bicubic，ANR[14]，A+[15]及LRANR[20].ANR，A+，LRANR使用相同参数的K-SVD字典，字典冗余度设为1024，采样窗口大小为3×3，并使用PCA对输入样本降维，双稀疏字典采样窗口大小3×3，直接使用未降维的样本训练，正则化参数λ设置为0.001，τ设置为0.005，迭代次数J设为10次，放大系数s设为3倍.由于人眼对自然图像的亮度敏感性，实验过程中RGB图片均转换到YCbCr颜色空间，并在亮度通道Y上进行实验，其它2个通道仅使用双三次插值放大.训练集选择Yang91[9]，并选择6张常用图片作为测试图片验证算法效果.我们使用PSNR和SSIM作为最终重建质量评价指标.

表1为本文方法和选取的对比方法在亮度通道上PSNR和SSIM指标对比情况.从表1可以看出，在放大系数为3的情况下，本文方法在六张测试图片上的客观评价指标均有一定提升，平均PSNR值比ANR，A+及LRANR分别提高了0.96，0.28以及0.16，平均SSIM值比ANR，A+及LRANR分别提高了0.013 5，0.003 2以及 0.001 9.

表2为双稀疏模型和K-SVD方法的误差比较情况.两者均在Yang91训练集上进行训练，字典训练参数设置与上述实验参数设置一致，分别在 10 000，20 000，30 000，40 000样本上计算误差并比较.误差计算公式如下：

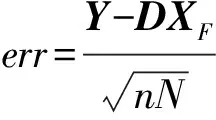
(11)

其中Y表示样本矩阵，D表示字典，双稀疏模型中D=ΦA，X表示表示系数矩阵，n表示样本维数，N表示样本总数.根据表2我们可以看出，相同字典训练参数设置下，相同样本数量下双稀疏模型表示误差均比K-SVD小，说明双稀疏模型对样本的表示能力更好.

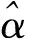
表1 各方法PSNR和SSIM比较

表2 不同样本数下双稀疏模型和K-SVD误差比较 (×10-3)

如表3所示，我们选择Lenna图片对本文算法引入的双稀疏字典模型以及非局部自相似性分别比较对最终重建结果的数值影响，结合表2可以看出，双稀疏字典相比于K-SVD字典重建误差更小，重建图像的PSNR指标也更高，同时图片的非局部自相似性约束也有利于重建质量的提升.

表3 Lenna各因素影响比较

图2到图4为各个方法放大3倍时在主观视觉效果上的对比，其中图(a)到(f)分别为原始HR图像，Bicubic重建SR图像，ANR重建SR图像，A+重建SR图像，LRANR重建SR图像以及本文算法重建SR图像.由图可以看出，Bicubic重建效果最模糊，ANR方法虽然较Bicubic图像质量有所提高，但仍存在比较明显的锯齿效应，A+及LRANR消除了锯齿效应，但边缘细节过于平滑，本文算法通过引入非局部自相似性约束，保留了图像的结构化信息，克服了上述边缘平滑问题，使重建细节信息得到了较好的保留，边缘更加清晰，且锯齿效应基本消除.

3 结语

本文提出了基于一种双稀疏模型和非局部自相似性约束的图像超分辨率方法，通过引入双稀疏字典模型，避免了信号降维过程的信息损失，同时重建阶段引入图像非局部自相似性约束，迭代求解最佳重构图像.实验结果表明，该算法对比多种超分辨率方法在客观评价指标上获得了一定提升，并且在主观视觉效果上，该算法获得了更好的边缘清晰度及细节信息.