采用稀疏表示和小波变换的超分辨率重建算法

张健， 黄德天， 林炎明

(华侨大学 工学院， 福建 泉州 362021)

超分辨率重建是根据给定的低分辨率(LR)图像及其先验知识恢复出高频细节.基于稀疏表示的超分辨率(SR)算法涉及两个阶段，即字典学习和稀疏编码.Yang等[1]开创性地将压缩感知运用到超分辨率算法中，首先，从LR和高分辨率(HR)图像块中学习联合字典；然后，计算LR图像块的稀疏系数；最后，将HR字典和稀疏系数线性组合来表示重建的HR图像块.Zeyde等[2]在文献[1]的基础上进行改进，利用主成分分析法(PCA)对提取的特征进行降维，采用不同的方法训练字典，并用正交匹配追踪(OMP)算法[3]求解稀疏编码模型,从而获得更好的重建效果，并在一定程度上提高了重建速度.

由于小波变换具有多方向性、多尺度性等特性，能分离出图像的高频和低频信息，Nazzal等[4]把小波变换运用到字典训练和图像重建中.Chang等[5]把流形学习中的局部线性嵌入(LLE)方法引入SR算法中，得到的重建图像较好地保留了原始图像的流形结构.Dong等[6]利用图像的局部与非局部信息，在稀疏编码阶段分别引入自回归(AR)与非局部(NL)自相似正则化项，提升了重建图像的边缘细节.图像的非局部相似性最早由Efros等[7]提出，随后被广泛应用于图像去噪和复原.Chen等[8]将非局部自相似和局部光滑先验同时加入超分辨率算法中，并用分裂Bregman迭代优化算法求解目标函数，取得较好的重建效果.Dong等[9]综合考虑图像的非局部相似性和多尺度相似性，并将其融入压缩感知模型，取得了良好的重建效果.Huang等[10]改进了稀疏自动编码器，将其应用于超分辨率算法，该算法能有效地重建真实的医疗图像，恢复出更精细的边缘和纹理等细节.Wu等[11]利用PCA训练4组子字典，分别描述低频子图和3幅高频子图之间的关系.Ayas等[12]提出一种新型超分辨率重建算法，通过构建包含小波域中重要信息的字典恢复重建图像中的高频信息.考虑到在图像经小波分解后，边缘和纹理信息主要集中在3个HF子图上，王相海等[13]通过所提出的多角度模板对每个细节子图进行插值.上述3种算法重建的边缘和纹理信息更准确.对于磁共振成像，图像的分辨率、信噪比和扫描时间是3个相互制约的因素，它们不可能同时达到最优的状态.因此，磁共振设备捕获到的磁共振图像(MRI)通常是低分辨率的.Plenge 等[14]比较了6种SR方法与直接采集高分辨率MRI方法的性能，结果表明，SR方法能有效地平衡上述3个制约因素，比以增加扫描时间或降低图像分辨率为代价采集MRI更具优越性.因此，SR重建能经济有效地提高MRI的分辨率.

近年来，大量基于学习的MRI SR方法[15-22]利用学习的图像先验知识作为约束，解决图像重建的不适定逆问题.受上述文献的启发，结合小波变换的多尺度特性、多方向性与稀疏表示的灵活性，本文提出一种基于稀疏表示和小波变换的超分辨率算法.

1 超分辨率重建算法

借鉴Nazzal等[4]提出的SR方法，先对待重建图像进行小波分解;然后，对3个不同方向特性的高频子图分别进行超分辨率重建;最后，对重建得到的高频子图进行逆小波变换，得到最终的HR重建图像.此外，为了充分利用图像的高频信息，将小波变换运用于字典训练中，分别训练水平、垂直、对角方向的字典对(Dil，Dih)，i=h，v，d代表水平、竖直和对角线3个方向.

1.1 稀疏编码模型

为了提升超分辨率算法的性能，在对冗余字典下的图像系数进行稀疏约束的同时，对重建的高频子图像也进行稀疏约束，从而建立一种双稀疏编码模型.考虑到自然图像通常具有复杂的结构特征，仅使用单一的稀疏性作为约束条件无法重建出高质量的图像.因此，为了保留图像的流形结构，在双稀疏编码模型中加入局部线性嵌入正则化项(LLER).

1.1.1 双稀疏编码(DSC)模型 除了图像在学习字典下的系数必须是稀疏的，考虑到重建后的高频图像同样具有稀疏性，在稀疏编码的阶段，不仅对冗余字典的系数进行稀疏约束，同时对重建得到的高频信息也进行稀疏约束，并由此建立双稀疏编码模型，即

(1)

式(1)中：αmh，αml分别是HR和LR子图的稀疏系数；Dmh，Dml分别是HR和LR的子字典；Dhα是重建得到的高频图像；wm(m=h，v，d)代表水平、竖直和对角线3个方向的LR细节子图；λ是正则化参数，用于平衡稀疏系数的稀疏性和wm的保真度；β是正则化参数，用于平衡小波域的稀疏性权重，并且对噪声具有鲁棒性.

根据HR细节子图的稀疏系数与LR细节子图的稀疏系数相同的假设[9]，令αmh=αml=αm，那么DSC模型可改写为

(2)

图1 重建流程Fig.1 Flowchart of reconstruction

将待重建的图像经小波分解得到1幅低频子图与3幅高频子图，由于高频子图对应的高频信息具有稀疏性，所以，通过式(1)分别对3个高频信息进行重建.对重建后的3幅高频子图(LH，HL，HH)和LR低分辨图像再进行逆小波变换，得到最后的高分辨率图像，其重建流程，如图1所示.

1.1.2 局部线性嵌入正则化 在基于稀疏表示的SR算法中，图像结构信息的丢失或不足将导致重建后的图像缺乏明显的结构特征，且若图像的流形结构能够被保留，则可以为后续的图像重建提供足够的结构信息.因此，为了更好地保留图像原有的流形结构，在稀疏编码过程中加入LLE正则化项.LLE是流形学习中的经典算法，在处于同一流形的前提下，该方法假设LR图像能够由其最近邻线性表示，那么，相应的稀疏系数也能通过相应的近邻点使用相同的权值线性表示.重构权值qmi，j可表示为

(3)

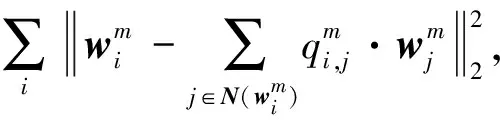
‖(I-Qm)Wm‖22.

(4)

在双稀疏模型中加入流形学习正则化项(式(3))，即

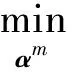
(5)

式(5)中：η是正则化参数.

(6)

式(6)等价于

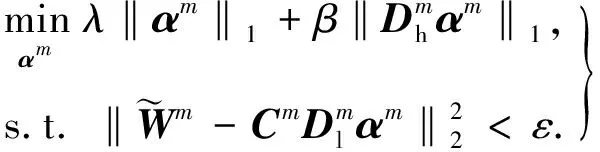
(7)

式(7)可优化为

(8)

通过分裂Bregman算法[23]将式(8)转化为

(9)

算法1用于求解LLER-DSC模型的分裂Bregman算法步骤如下.

输入:LR字典Dml，HR 字典Dmh和小波细节子图wm.初始化λ，β，η，μ1，μ2，f0，m=0，b0，m=0.

输出:稀疏表示系数αm.

如果没有收敛，则

fk+1，m=fk，m+(Dmlαk+1，m-wm)；

结束.

1.2 基于小波域的字典训练

小波变换对图像进行多尺度分解，它可以聚焦到图像的任意细节.将小波变换运用到字典训练阶段有两个原因:1) 因为小波本身具有多尺度和多方向等特性，所以使用经小波分解得到的子图进行字典训练，得到的字典同样具有这些特性，从而使重建图像具有更清晰的边缘；2) 由压缩感知理论可知，图像本身或其在某个变换域内的表示越稀疏，经超分辨率算法得到的重建图像质量就越好.

对每一幅图像进行小波分解，得到LL1，LH1，HL1和HH14组子图，其中，LL1是和原图相似的低频子图;LH1,HL1和HH1分别代表水平、竖直和对角线方向的高频子图，这些高频子图具有稀疏性.将其中的3组高频子图用于训练高分辨率的字典;然后，对LL1进行二级小波分解，并将得到的3组高频子图LH2，HL2和HH2作为低频部分，用于训练低分辨率的字典.

借鉴文献[2]分别训练高、低分辨率字典的思想，但没有使用高通滤波器进行特征提取.这是因为经过小波变换后的图像已经提取了高频特征，不需要再单独进行特征提取.低分辨率字典的训练有以下5个步骤.

步骤1分别对每组子图LH2,HL2和HH2进行逆小波变换(保留其中1幅高频子图，同时将其他3幅子图置零)得到3组子图LH′2,HL′2和HH′2，这样就能保证在求解稀疏系数时图像维度一致.

步骤2对3组子图LH′2,HL′2和HH′2重叠分块.

步骤3对这些图像块进行列向量化，得到Pil(i=LH，HL，HH).

步骤4为了减少字典训练量，采用PCA对Pil进行降维处理.

步骤5使用K-SVD算法进行字典训练，有

(10)

式(10)中：αi是高频子图的稀疏系数；S是最大稀疏度.

相应的高分辨率字典的计算式为

Dih=PihαiT(αi(αi)T)-1.

(11)

式(11)中：上标T代表转置；上标-1代表逆运算.

最后，得到3对高、低分辨率字典(Dil，Dih)，i=h，v，d.其中，(Dhl，Dhh)，(Dvl，Dvh)，(Ddl，Ddh)分别是水平方向、垂直方向、对角线和反对角线方向的高、低分辨率字典.

1.3 算法的具体步骤

在文中算法中，对于给定的一幅低分辨率图像，其超分辨率的问题就转换成对小波变换得到的3幅高频子图进行重建(图1).相对于传统的基于稀疏表示的超分辨率算法，文中算法利用小波变换在分析图像细节方面的优势，使最终得到的重建图像包含更多的细节信息.文中算法有以下4个具体步骤.

步骤1对待重建的图像进行一级小波分解得到LL,LH,HL和HH 4幅子图.

步骤2分别对LH,HL和HH 3幅高频子图进行逆小波变换(保留其中1幅高频子图，同时将其他3幅子图置零),得到LH′,HL′和HH′，这样有助于维持每个小波子带的相同方向性.

步骤3采用式(6)对应的稀疏编码模型对LH′,HL′和HH′子图进行重建.先对这3幅子图进行重叠分块，并将其列向量化;然后，根据不同特征的图像块，自适应地选择训练好的字典，并求出对应的图像块稀疏系数.假设高频子带的稀疏系数和低频子带的稀疏系数相同，那么，高频子带对应的重建图像块计算式为Pih=Dilαi.最后，将具有相同方向特征的重建图像块(重叠区域取平均)分别融合成一幅子图(LH″，HL″和HH″).

步骤4对重建得到的3幅子图和LR图像进行逆小波操作，得到最终的HR重建图像.

2 实验结果与分析

2.1 实验环境及数据准备

采用的硬件平台为Intel(R) Core(TM)i7-7700K CPU@4.20 GHz，内存24.0 GB，软件平台为Windows 64位操作系统，仿真软件为MATLAB 2016b.在重建图像过程中，选取图像块大小为6 px×6 px，在邻近块之间的重叠区为1个像素；在算法1中，λ=3.25，β=0.01，μ1=0.001，μ2=0.010.

用于字典训练的图像集采用文献[1，24-26]中均使用的含有91张高分辨率图像的训练集.为了保证实验的客观性，采用的测试图像库为Set5[27]，Set14[2]，B100(BSDS300[28]中取100张)，这些测试图像专门用于评价超分辨率重建算法.同时，还将文中算法运用到磁共振图像中，为了保证用于MRI图像实验的客观性，训练图像来源于TCIA[29]，测试图像也从中随机挑选.为了验证文中算法的有效性，主要与双三次插值(Bicubic)、L1SR[1]算法、SISR[2]算法、ANR[25]算法、LLE[30]算法、文献[31]算法和SRISAE[32]算法进行比较.重建图像的评价主要包括主观和客观评价两个方面.客观评价主要采用峰值信噪比(RPSN)[33]和结构相似度(MSSI)[34]两个指标.峰值信噪比和结构相似度的分别定义为

2.2 结果分析

为了方便定量评价重建图像的质量，将测试图像经过小波变换得到的LL子图作为待重建的LR图像，并将原始的HR图像作为参考图像.实验分为3组:1) 验证改进算法的有效性；2) 对自然图像进行超分辨率重建；3) 将文中算法运用于磁共振图像.

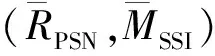
表1 4种SR算法的RPSN和MSSI的平均值比较Tab.1 Comparison of average RPSN and MSSI values obtained by four different SR algorithms

由表1可知：2种改进算法的RPSN平均值都优于SRWD算法，其中，LLER-DSC算法得到了最好的重建结果.由此可知，基于双稀疏改进的SR算法是有效的.

2) 第2组实验.该实验的目的是验证文中算法(LLER-DSC)对自然图像重建的有效性.将文中算法与Bicubic，SRISAE,SISR，ANR，NE_LLE，文献[31]，SRISAE算法进行比较.上述7种SR算法在Set5，Set14和B100中的RPSN和MSSI的平均值比较，如表2所示.由表2可知：在量化结果上，文中算法都优于其他比较算法.由此可看出，文中算法重建效果高于其他比较算法.

表2 7种SR算法的RPSN和MSSI的平均值比较Tab.2 Comparison of average RPSN and MSSI values obtained by seven different SR algorithms

不同SR算法获得的重建Butterfly和Barbara的主观比较结果，如图2，3所示.图2,3中：除了列出原始HR参考图像和上述7种对比算法重建结果在同一区域的细节放大图外，还列出SRWD和DSC算法的重建结果.

图2 不同SR算法获得的重建Butterfly的主观比较结果Fig.2 Visual comparison results of reconstructed images obtained by different SR algorithms for Butterfly

图3 不同SR算法获得的重建Barbara的主观比较结果Fig.3 Visual comparison results of reconstructed images obtained by different SR algorithms for Barbara

由图2,3可知：Bicubic不能重建出清晰的图像；SISR,NE_LLE,文献[31]和SRISAE算法的重建图像边缘过于平滑，丢失了部分信息；6种对比算法中，ANR的重建结果最好，但仍然不够清晰；相比SRWD和DSC算法，LLER-DSC算法的重建图像更清晰，LLER-DSC算法能有效地减少重建图像的失真并且生成更精确的细节信息，重建出更接近于原始HR的图像.该组实验进一步说明了文中算法的鲁棒性和有效性.

3) 第3组实验.由于MRI的分辨率通常受到许多因素的限制，如信噪比、硬件条件、扫描时间及患者的舒适度等，导致采集到的图像都是低分辨率图像.然而，在许多医学应用中，通常需要清晰的高分辨率MRI来辅助医生，以提高临床诊断的准确性.所以，该组实验将文中算法应用到MRI图像的超分辨率重建中，从而验证文中算法的实用性.从癌症影像档案(TCIA)[29]中随机选取91幅高分辨率MRI图像作为训练图像，测试图像也从TCIA中随机挑选.不同SR算法对MRI重建图像的RPSN和MSSI值的比较，如表3所示.由表3可知：文中算法的RPSN和MSSI值总体上优于其他算法，并且两个评价指标的平均值都最高.

表3 不同SR算法对MRI重建图像的RPSN和MSSI值的比较Tab.3 Comparison of RPSN and MSSI of reconstructed MRI images obtained by different SR algorithms

不同SR算法获得的重建MRI图像Prostate-11,Prostate-02的主观比较结果，如图4,5所示.由图4,5可知：NE_LLE算法得到的图像在边缘细节方面恢复不明显，且出现严重的混叠现象；与其他SR算法相比，SISR算法重建的图像不够清晰；ANR算法在边缘锐化方面优于SISR算法，但是其重建图像出现了许多虚假细节；相比于ANR算法，文献[31]算法重建的图像具有较少的虚假细节，且其恢复的边缘细节更好；相比于文献[31]算法，SRISAE算法重建图像的边缘细节有进一步提升；LLER-DSC算法在边缘细节的恢复方面略优于SRISAE算法，尤其是水平、垂直和对角方向的边缘较为明显，得到的重建图像也更为清晰.因此，文中算法在MRI图像超分辨率重建中取得了令人满意的结果.

图4 不同SR算法获得的重建MRI图像Prostate-11的主观比较结果Fig.4 Visual comparison results of reconstructed MRI images obtained by different SR algorithms for Prostate-11

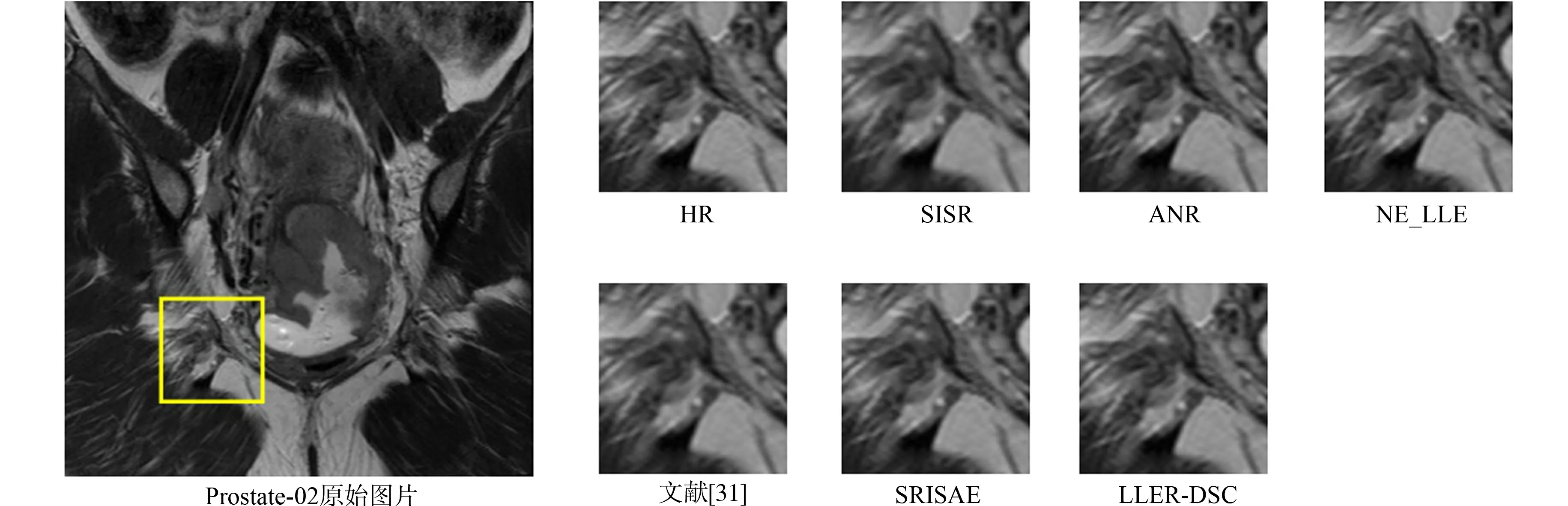
图5 不同SR算法获得的重建MRI图像Prostate-02的主观比较Fig.5 Visual comparison results of reconstructed MRI images obtained by different SR algorithms for Prostate-02

3 结论

将小波变换运用到字典训练和稀疏编码阶段，提出一种基于稀疏表示和小波变换的图像超分辨率算法.通过结合小波分解得到的高频信息的稀疏性与图像在冗余字典下的系数的稀疏性，提出一种双稀疏编码模型，从而提高超分辨率算法的性能.为了保留图像的流形结构，在双稀疏编码模型中引入LLE正则化项.同时，为了充分利用图像的高频信息，将小波变换运用于字典训练的阶段，并分别对待重建图像经小波分解得到的3幅高频子图进行重建.

从主观和客观两个方面对重建结果进行分析，结果表明，文中方法的重建效果优于其他用于比较的方法.同时，还将文中算法运用于MRI图像的重建，同样获得了良好的效果.在实际应用中，文中算法有利于需要MRI快速成像的情况.由于对3幅高频子图的重建都采用相同的SR算法，并没有考虑每幅子图的差异性，因此，如何根据每幅高频子图的特征分别设计特定的SR算法，是将来工作的研究重点.