改进分析型嵌入原子法在W(100)表面声子谱中的应用*

张晓军 王安祥 严祥安 陈长乐

1) (西安工程大学理学院, 西安 710048)

2) (西北工业大学理学院, 西安 710072)

在表面晶格动力学理论的框架下, 采用改进分析型嵌入原子法模型模拟W(100)表面沿对称方向上的声子色散频谱, 并计算不同对称点处的极化矢量.按照表面模的判定依据和标记方法绘制不同对称方向上的表面模, 并讨论表面模的分布范围和模式耦合现象.基于计算所得的极化矢量, 构建近表面原子层的振动态分布, 分析不同对称方向上表面模的局域特征和极化方式.以极化矢量为考察对象, 直观、形象地展示了表面模色散支之间的避免交叉现象和独立性实交叉现象.

1 引 言

表面声子色散关系是获取固体表面相变、表面吸附、原子结构、原子间相互作用以及电子结构信息的重要手段[1].同时, 表面声子色散频率也是数值计算固体表面比热、自由能、态密度等固体表面热力学量的重要输入参数[2,3].鉴于此, 众多科研工作者一直致力于表面声子色散的实验和理论研究[4−9].实验测量技术, 如电子能量损失谱 (electron energy loss spectroscopy, EELS)和氦原子非弹性散射 (Helium atom scattering, HAS), 以及它们的衍生方法已被广泛应用于测量各种表面(如清洁表面、吸附表面、重构表面等)的声子色散关系[4−7].然而, 在实验中受探测方位的限制, 一些表面模却很难探测到, 如Cu(100)表面中的S6和S7表面模以及沿方向的 S1表面模[10,11].此外, 实验测量仅能给出不同波矢对应的色散频率, 却不能提供表面模极化和局域的相关信息.对于表面晶格振动的全面理解不仅需要声子色散频率和波矢之间的变化关系, 而且需要振动模极化方式和局域特征[12].这些信息均可通过对表面晶格振动的理论描述而获得.近十余年来, 在表面晶格动力学理论的框架下, 人们用各种相互作用势来描述表面晶格振动,如 Yndurain 等[13]和Łażewski等[14]曾利用第 1 原理 (First Principles, FP)分别计算了 Pb(111)薄膜以及 Fe(100)、Fe(110)表面的声子谱, Benedek等[15]采用密度泛函微扰理论(density functional perturbation theory, DFPT)研 究 了 Al(100)和Cu(111)表面色散关系.Rusina 等[16]应用原始的嵌入原子法 (Embedded Atom Method, EAM)在考虑弛豫的情况下研究了Ni/Cu(100)薄膜的声子频谱.这些文献中均获得了不同对称方向上的声子色散关系, 通过与实验结果比较, 一方面检验了所用相互作用势模型的普适性, 另一方面验证了计算方法的正确性.同时, 这些计算结果全面展现了二维体系的声子色散关系, 弥补了实验探测的不足(尤其是弱表面模).然而, 在这些报道中并没有全面讨论振动模的极化方式和局域特征.分析原子的极化方式和局域特征, 能反映出原子间作用的更多信息, 进一步明确原子的振动状态.这些微观机制,为进一步研究固体表面材料的物理和化学性质提供数值依据.本文把改进分析型嵌入原子法模型势和表面晶格动力学理论相结合, 应用数值计算的方法, 模拟了 W(100)表面沿3 个高对称方向上的声子色散曲线, 构建了近表面原子层的振动态分布, 通过考察振动模的极化矢量和穿透深度, 讨论了表面模极化方式和局域振动的特点.

2 基本理论和模型

2.1 表面晶格动力学理论

在金属钨(W)晶体结构中抽取N层(100)取向的原子薄板, 以薄板晶面作为二维原子平面, 如图1(a)所示.图中实心圆表示第1层原子, 空心圆表示第 2层原子, 分别选取 [001]、[010]和 [100]方向作为W(100)表面结构的x、y和z方向.在选定的x-y二维坐标系中,是二维正格基矢.图1(b)是相应的二维倒格点阵, 其中是二维倒格基矢, 细实线表示W(100)表面的第一布里渊区, 粗实线表示布里渊区的最小重复单元.以为单位(a为晶格常数), 则二维布里渊区中对称点的倒格坐标依次为 ( 0,0) 、 ( 1,0) 和 ( 1,1).表示对称方向(波传播方向或波矢方向), 对应的群论符号依次为

在简谐近似下, 薄板中第 l原子层 (l = 1, 2, 3,···,N )的运动方程表示为[17]

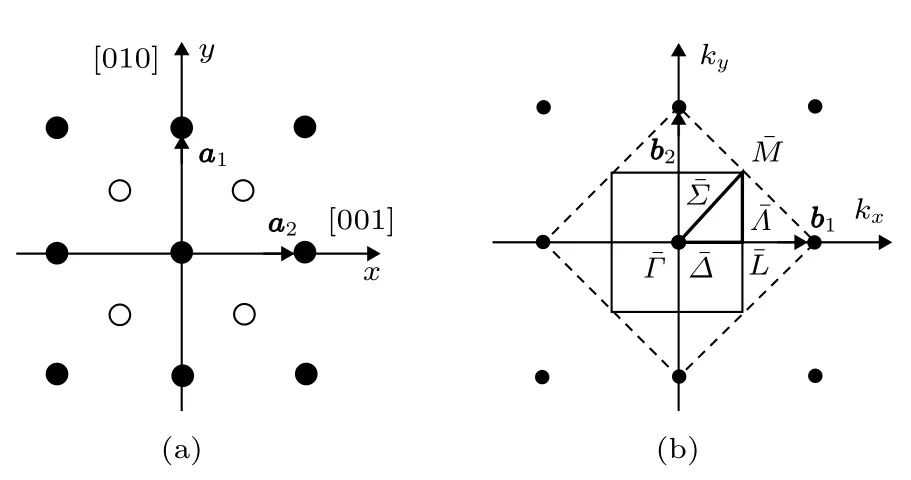
图1 W(100)表面结构 (a)正格点阵; (b)倒格点阵Fig.1.Surface structure of W (100): (a) Crystal lattice;(b) reciprocal lattice.

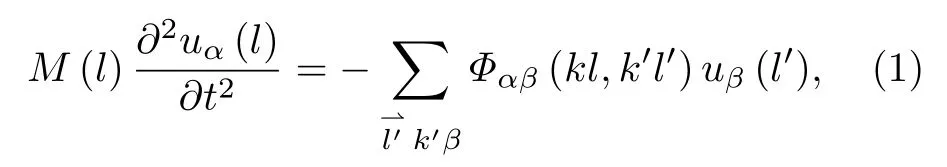
式中: M (l) 为第 l原子层中原子的质量; uα(l) 为第 l原子层沿 α 方向的瞬时位移; Φαβ(kl,k′l′) 是第l原子层和第 l′原子层间的力常数, 它的物理意义为当第 l′原子层中第 k′个原子在 β 方向上移动单位距离时, 第l原子层中第k个原子在 α 方向上所受的力, 其表达式为

在薄板体系中, 设定平行于表面的平移满足周期性边界条件, 因而薄板体系对二维波矢的平移保持不变, 则原子层的位移具有布洛赫函数形式[17]

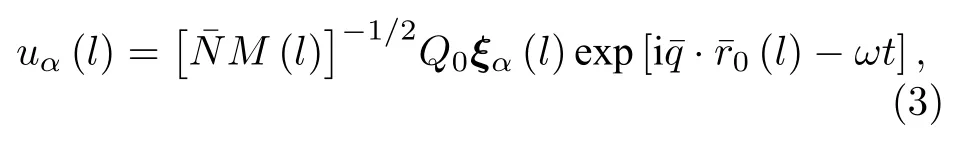
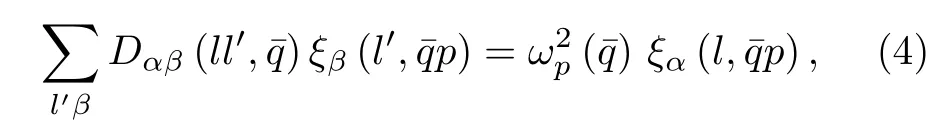
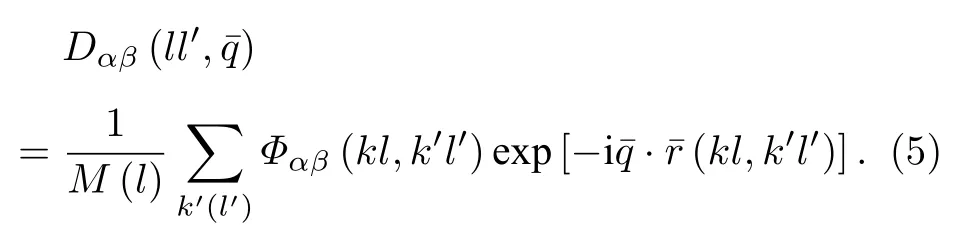
金属钨属于布拉菲晶格, 每一原胞含有一个原子, 则在 (4) 式中, 模式指标 p =1,2,···,3N , 于是具有 3 N 个分量, 对于确定的, 将有 3 N 个振动模式.显然, (4) 式是 ξ (l,p) 的 3N 个线性齐次方程, 因为晶格振动总是存在的, 故 ξ (l,p) 有非零解得条件是

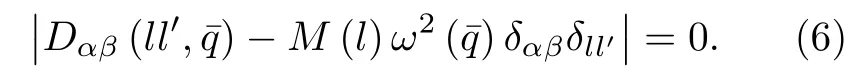
通过求解(6)式可获得表面振动频率随波矢的变化关系.

2.2 改进分析型嵌入原子法模型

张邦维、欧阳义芳和胡望宇等[19−21]在嵌入原子法(EAM)的基础上增加了非球对称能量修正项, 构建了具有解析形式的原子间相互作用势模型, 即改进分析型嵌入原子法(modified analytic embedded atom method, MAEAM)多体势模型,该模型已在原子层次材料设计方面得到广泛的应用[22−24].MAEAM 的基本公式为[19],

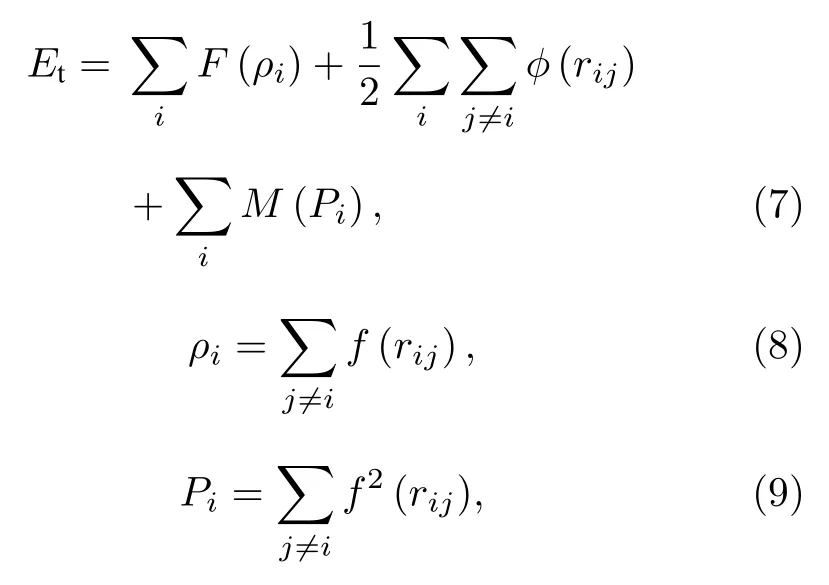
式中, Et是体系的总能量, F (ρi) 是在系体中嵌入原子i的嵌入能, ρi和 Pi是其他原子分别在原子i位置处产生的球形电子密度和非球形电子密度,f(rij)是原子j在原子i位置处产生的电子密度,rij和 ϕ (rij) 分别是原子i和原子j之间的相互作用距离和相互作用能, M (Pi) 是修正能, 表示原子电子密度非球形对称分布所引起的系统总能量的变化.嵌入函数 F (ρi) 、相互作用势 ϕ (rij) 、修正项函数 M (Pi) 和电子密度函数 f (rij) 的解析表达式可参看文献[21,22].

3 结果和讨论

3.1 表面弛豫

根据能量最小原理, 用改进分析型嵌入原子势模型计算了W(100)表面多层对称弛豫, 结果发现,原子层间变化呈现出振荡现象.相对于完整晶格(层间距为1.5825 Å), 第1原子层和第2原子层之间处于膨胀状态, 膨胀比为 ∆12=3.08% , 第 2原子层和第3原子层之间的压缩比为 ∆23=−0.90% ,而第3原子层和第4原子层之间也处于膨胀状态,膨胀比为 ∆34=0.76%.对于W(100)表面弛豫的实验研究和理论研究较少, 我们没有找到可行的实验资料进行比较, 在理论计算方面, 我们仅发现Fasolino等[25]曾利用有效两体势计算得到第1原子层和第2原子层之间的膨胀了0.01 Å, 这与我们的计算结果(0.048 Å)相差甚远.由于我们考虑多体相互作用, 因此计算结果大于Fasolino等[25]的计算值是合理的.

3.2 W(100)表面声子谱

选取61层(100)取向的W原子薄板, 应用MAEAM计算弛豫后W(100)表面的面间力常数[26],以此为输入参数, 建立了 183 × 183维动力学矩阵.在第一布里渊区最小重复单元的范围内, 分别模 拟 W(100) 沿对 称 方 向 的 表 面声子谱, 结果如图2所示.图中, 纵坐标表示原子的振动频率, 横坐标表示二维约化波矢约化波矢分量其中 qαm是对称方向上波矢在 α 分量上的最大值, 横向箭头表示波传播方向或约化波矢增大的方向.

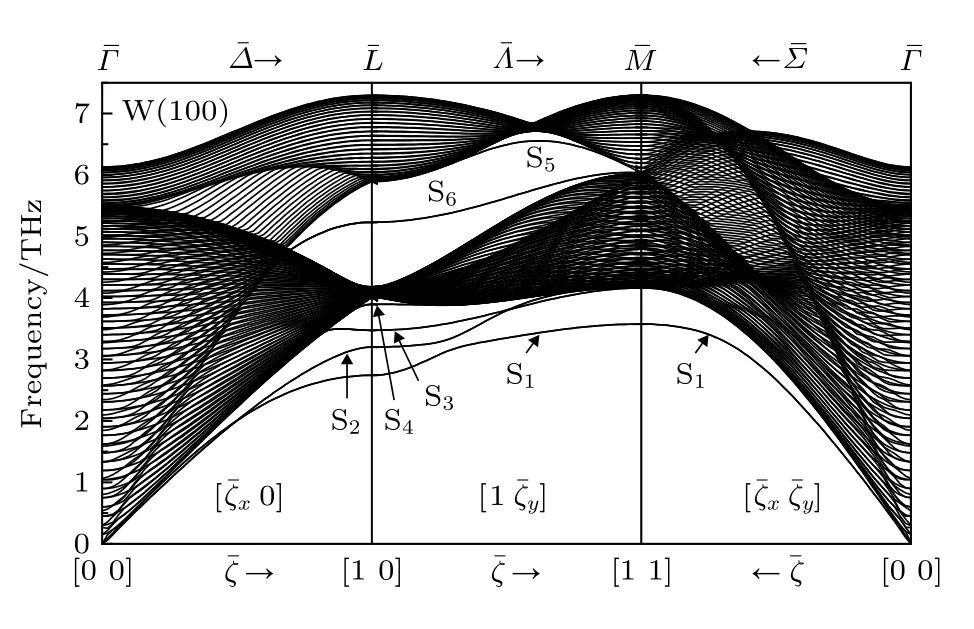
图2 W(100)表面声子谱Fig.2.Surface phonon spectrum of W(100).

当波矢确定时, W(100)原子薄板(61层)有183个振动频率, 对应183种振动模.根据振动模的极化方式、色散支的分布以及振幅的穿透深度,振动模可分为体振动模(简称体模)和表面振动模(简称表面模).振动能量或振幅分布于整个薄板内且极化方式与周围模式一致的振动模称为体模[18].当波矢一定时, 所有体模对应的频率形成一个频带, 称为体子模带.随着波矢的增加或减小, 体子模带横向扩展形成体模带(图2中黑色阴影区域),体模带以外的空白区域称为禁带, 被体模带包围的禁带称为带隙或带沟(如图2).体模带是准连续的,随着原子层数的增加, 体模逐渐增多, 准连续的体模带逐渐趋于连续.与体模不同, 表面模局域在表面附近, 其振幅会随原子层数的增加而减弱.具有以下任一特征的振动模均可判定为表面模[12,17]:1)从体模带的最下边缘或最上边缘剥离出来, 位于禁带中的振动模; 2)从带隙的边缘处分离出来,位于带隙中的振动模; 3)位于体模带内, 但其极化方式与周围体模极化方式不同的振动模; 4)位于体模带内, 且极化方式与周围体模的极化方式相同, 但振幅会随原子层数的增加而衰减.具有第4种特征的表面模因受到体模的扰动而杂化[18], 其极化方式与体模没有区别, 这类表面模又称为混合模或伪表面模.

按照表面模的判定依据和Allen等[18]的标记方法, 绘制了W(100)表面沿对称方向上的表面模分布, 如图3 所示.沿方向存在 7 种表面模, 分别为 S1、S2、S3、S4、S6、S7和 MS8表面模.S1, S2,S3和S4表面模从体模带的下边缘剥离出来, 位于体模带的下方.其中S1表面模和S2表面模存在于整 个方 向, 当时, S1表面 模色 散支 和S2表面模色散支相互交叉, 频率简并为2.01 THz,随着波矢的增大, S1和S2表面模色散支相互分离,这种现象称为独立性实交叉(将在3.3节中详细说明).S3表面模和S4表面模分布于点附近较小的波矢范围内, 随着波矢不断减小, S3和S4表面模分别在约化波矢等于0.84和0.93处进入体模带并同化为体模, 不再具有表面模的特征.在点附近狭小的波矢范围内存在S7表面模, 它位于体模带的下方并紧挨着体模带的边缘(图3).在W(100)表面的振动频谱中仅有一个带隙, 即S1(100)带隙,一部分S1(100)带隙落在方向上.S6表面模分布在带隙内(即带隙模), 其对应的约化波矢范围为 0.7—1.0.当时, S6表面模进入体模带后丧失了表面特性而演变成体模.点附近, 靠近带隙下边缘的体模带中存在伪表面模MS8, 其分布范围很小且完全淹没在体模带中(如图3).

图3 W(100)表面模分布Fig.3.Surface mode distribution of W(100).

图4 S1 表面模的计算结果和实验值的比较Fig.4.Comparison of calculated S1 surface mode and experimental value.

实验中, Ernst等[28]曾采用氦原子散射法测量了W(100)表面声子色散关系, 得到S1表面模(瑞利模) 沿方向的部分测量值, 其结果连同现在的计算结果一并绘制在图4中.图中实心圆点表示实验数据, 实线表示计算所得的表面模, 点线表示体模带边界.从图4可以看出, 计算所得的S1表面模与实验结果基本一致, 特别沿方向约化波矢范围内以及 沿方向约化波矢范围内, 声子频率很好地再现了实验结果.其他约化波矢范围内, 计算的声子频率整体上低于实验结果, 但相应的声子色散曲线与实验点线具有相似的形状.计算结果和实验值的偏差可能是由于现在的计算值是在简谐近似下所得, 而且没有考虑表面电子态对动力学矩阵的贡献[12], 而实验测量中并没有忽略这些效应.

除了S1表面模外, 没有可行的实验结果与计算值进行比较, 幸运的是, Joubert[29]和 Fasolino等[25]曾分别采用紧束缚法 (tight binding method,TBM)和有效哈密顿法 (Effective Hamiltonian Approach, EHA)计算了W(100)表面的声子谱.表1中列出由3种模型所得到的高对称点(和)处表面模的振动频率.从表中可以看出,MAEAM的计算结果普遍偏小, 最大偏差为0.58 THz (S1表面模).考虑到由 MAEAM 得到的膨胀比( ∆12=3.08% )大于EHA和TBM的计算值(EHA中 ∆12=0.67% , TBM中未考虑表面弛豫), 而膨胀比越大, 面间力常数越小[27], 会导致振动频率变小, 因此MAEAM计算的结果更加合理.

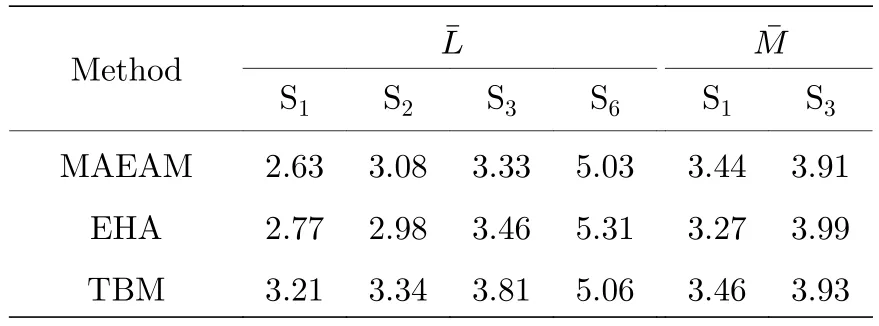
表1 高对称点处 W(100)表面模振动频率的比较 (单位: THz)Table 1.Comparison of vibration frequencies of surface modes for W(100) at high symmetry points(in units of THz).

3.3 W(100)表面模的振动特征

为了讨论W(100)表面模的局域特征和极化方式, 在W(100)表面声子谱的基础上, 计算了W(100) 表面沿对称方向上不同对称点的极化矢量, 构建了近表面原子层的振动态分布.图5是W(100)近表面原子层沿对称方向的局域振动态密度.图中z轴表示极化矢量的平方[18,30]|ξ(l)|2=|ξx(l)|2+|ξy(l)|2+|ξy(l)|2, 其中 l是原子层指数, l =1,2,3,··· 分别对应第 1原子层、第2原子层、第3原子层…, x轴表示原子层振动频率, y轴表示约化波矢.

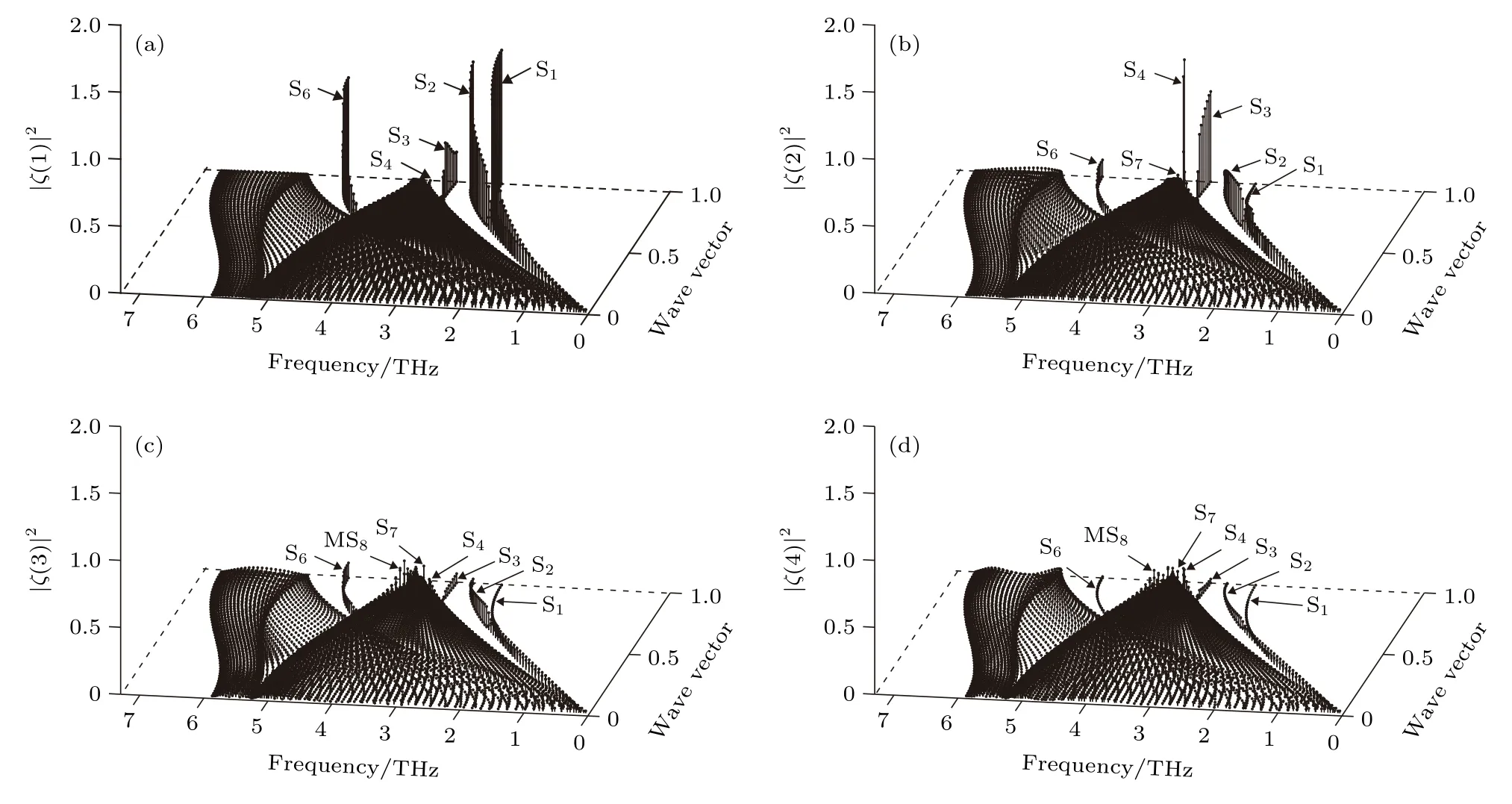
图5 W(100)近表面原子层沿对称方向的局域振动态密度 (a)第 1 原子层; (b)第 2 原子层; (c)第 3 原子层; (d)第 4 原子层Fig.5.Local vibrational state density of atomic layers in the vicinity of the W (100) surface along symmetry direction:(a) First atomic layer; (b) second atomic layer; (c) third atomic layer; (d) fourth atomic layer.

图6 W(100)近表面原子层沿 对称方向的极化态密度 (a)第 1 原子层沿 x 方向极化; (b)第 1 原子层沿 y 方向极化; (c)第1原子层沿z方向极化; (d)第2原子层沿x方向极化; (e)第2原子层沿y方向极化; (f)第2原子层沿z方向极化Fig.6.Polarizing state density of atomic layers in the vicinity of the W (100) surface along symmetry direction: (a) x polarization for first atomic layer; (b) y polarization for first atomic layer; (c) z polarization for first atomic layer; (d) x polarization for second atomic layer; (e) y polarization for second atomic layer; (f) z polarization for second atomic layer.

图7 W(100)近表面原子层沿 方向上的局域振动态密度 (a)第 1 原子层; (b)第 2 原子层; (c)第 3 原子层; (d)第 4 原子层Fig.7.Local vibrational state density of atomic layers in the vicinity of the W (100) surface along symmetry direction:(a) First atomic layer; (b) second atomic layer; (c) third atomic layer; (d) fourth atomic layer.

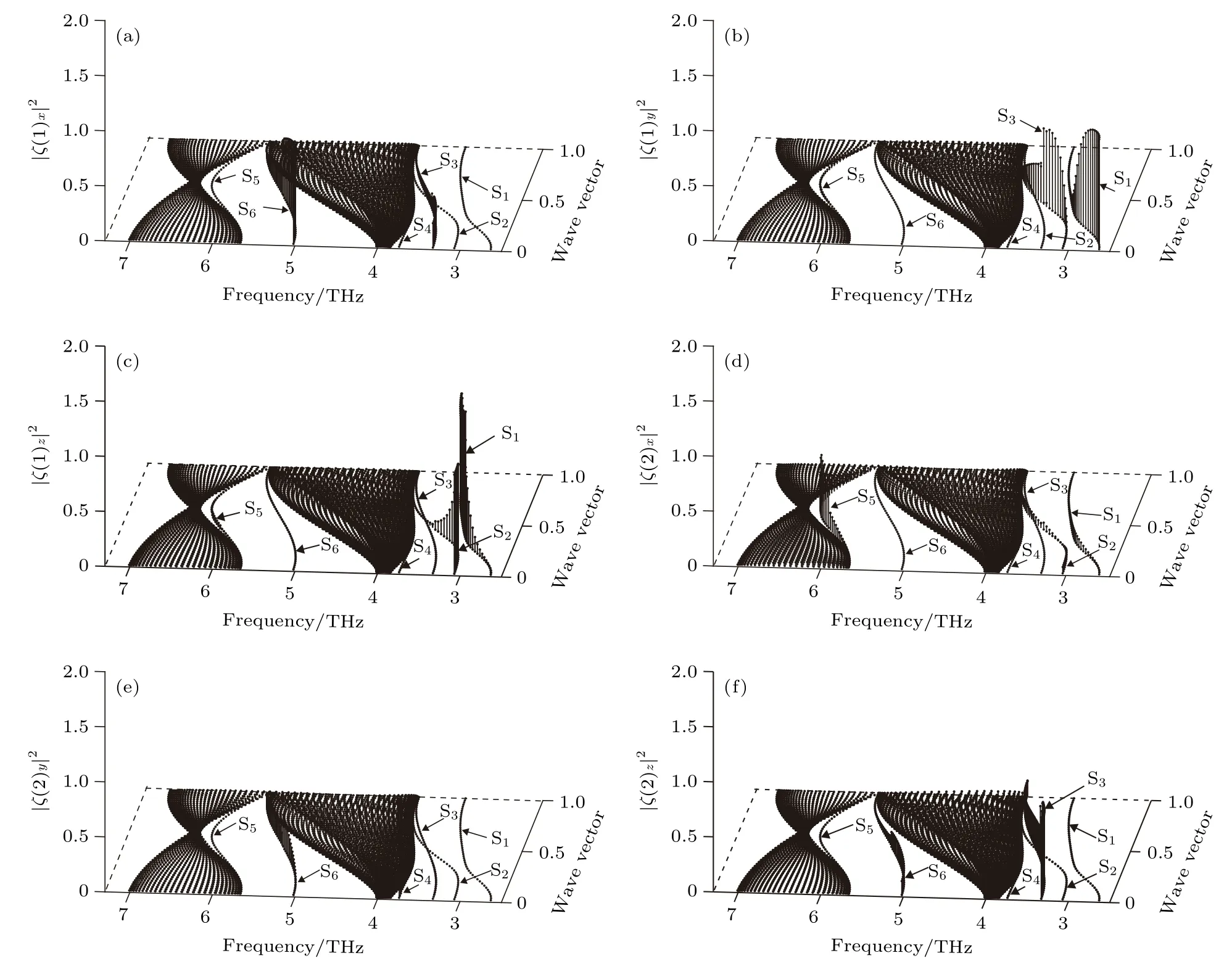
图8 W(100)近表面原子层沿 方向的极化态密度 (a)第 1 原子层沿 x 方向极化; (b)第 1 原子层沿 y 方向极化; (c)第 1 原子层沿z方向极化; (d)第2原子层沿x方向极化; (e)第2原子层沿y方向极化; (f)第2原子层沿z方向极化Fig.8.Polarizing state density of atomic layers in the vicinity of the W (100) surface along symmetry direction: (a) x polarization for first atomic layer; (b) y polarization for first atomic layer; (c) z polarization for first atomic layer; (d) x polarization for second atomic layer; (e) y polarization for second atomic layer; (f) z polarization for second atomic layer.

图9 W(100)近表面原子层沿 方向上的局域振动态密度 (a)第 1 原子层; (b)第 2 原子层Fig.9.Local vibration state density of atomic layers in the vicinity of the W (100) surface along symmetry direction: (a) First atomic layer; (b) second atomic layer.

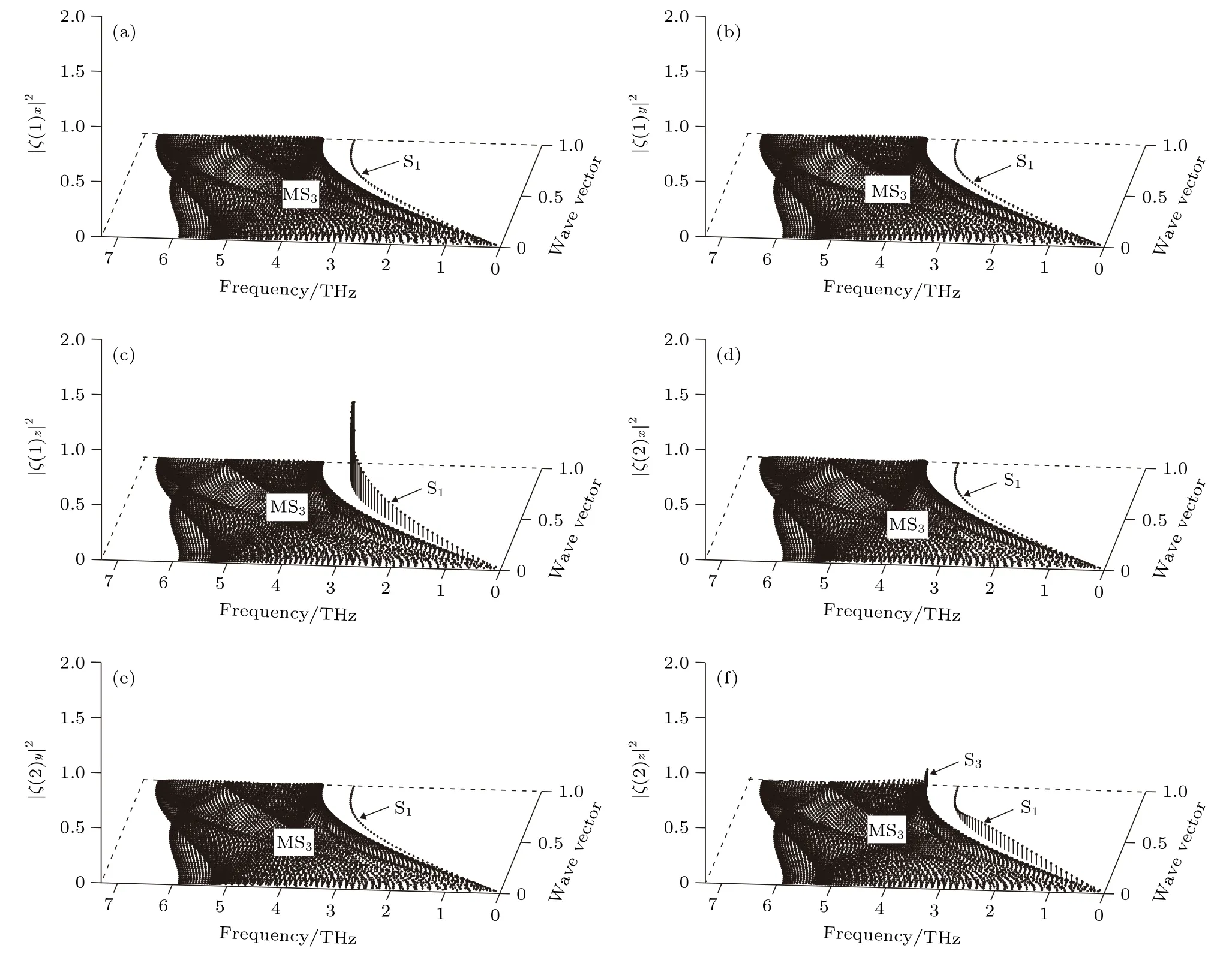
图10 W(100)近表面原子层沿方向的极化态密度 (a)第1原子层沿x方向极化; (b)第1原子层沿y方向极化; (c)第1原子层沿z方向极化; (d)第2原子层沿x方向极化; (e)第2原子层沿y方向极化; (f)第2原子层沿z方向极化Fig.10.Polarizing state density of atomic layers in the vicinity of the W (100) surface along symmetry direction: (a) x polarization for first atomic layer; (b) y polarization for first atomic layer; (c) z polarization for first atomic layer; (d) x polarization for second atomic layer; (e) y polarization for second atomic layer; (f) z polarization for second atomic layer.

4 结 论

表面声子谱是表面振动的量化表现, 是研究表面振动和表面物理性质的桥梁.因此要得到表面性质的微观机理和物理图景, 必须先细致研究表面声子谱.本文在表面晶格动力学理论的框架下, 采用改进分析型嵌入原子法模型模拟了W(100)表面沿对称方向上的声子谱, 绘制了表面模的分布图, 构建了近表面原子层的振动态分布, 讨论了不同对称方向上表面模的极化方式和局域特征.结果表明: 1) 沿对称方向上分别存在 7种、8种和 3种表面模.2)沿方向, 当约化波矢等于0.5时, S1表面模色散支和S2表面模色散支之间存在独立性实交叉, 简并频率为2.01 THz.交叉前后S1表面模和S2表面模的极化方式和局域特征没有发生改变.3)沿方向, S1表面模色散支和S2表面模色散支在约化波矢等于0.32附近存在避免交叉现象, 在避免交叉位置处, S1表面模和S2表面模的极化方式进行了交换, S1表面模由y方向极化变为z方向极化,S2表面模由z方向极化变为y方向极化.4)沿方向, S2表面模色散支和S3表面模色散支在约化波矢等于0.5处发生独立性实交叉, 交叉前后两表面模的极化方式和局域特征不受影响.5)在和方向存在MS8伪表面模, 而在方向存在MS3伪表面模, 这些伪表面模通常在各原子层的能量较小, 穿透深度较大, 属于弱表面模.