基于自适应转动惯量VSG 的微电网稳定控制

朱作滨 黄绍平

(1. 江西工程学院人工智能学院 新余 338000； 2. 湖南工程学院电气与信息工程学院 湘潭 411100)

1 引言

微电网由分布式电源、储能装置、控制装置、逆变装置、保护装置和负荷等组成，可运行于并网和孤岛两种模式。并网运行时，微网系统频率稳定由大电网提供支撑；孤岛运行时，系统频率的稳定完全依靠自身来维持。随着大量分布式电源接入电网，引入大量的电力电子变流器，由于电力电子装置本身不具备调频及调压特性，将会导致电网系统的不稳定性[1]。由于虚拟同步机(Virtual synchronous generator，VSG)控制技术能够模拟同步发电机的调频及调压特性，可以改善系统的稳定性而成为研究热点，受到广泛关注。

研究人员对VSG 控制技术进行了大量研究。文献[2]提出一种基于锁相环的虚拟同步发电机离/并网无缝切换控制策略，可模拟同步发电机的准同期并列装置，实现了一次调频以及离/并的平滑切换。文献[3]提出了VSG 构成的自主电力系统。文献[4]在VSG 的基础上，增加了原动机组和伺服机构，提出一种柔性虚拟调速器模型。与实际同步发电机并联运行时实现了功率均分。文献[5]将VSG技术应用于风电机组控制，实现了风电机组的调频特性，提高了系统频率的稳定性。文献[6]将VSG技术应用于光储并网系统中，实现了最大功率跟踪与调频特性的协调控制，提升了系统频率的稳定性。文献[7-8]提出一种自适应阻尼VSG 控制策略，抑制了系统输出频率及功率的振荡，提升了系统的稳定性。文献[9]对阻尼系数对VSG 系统稳定性机理进行了分析，得出阻尼系数对输出频率及功率振荡具有抑制作用。文献[10]提出一种孤岛型微网自适应转动惯量VSG 控制策略，提升了孤岛运行时微网系统频率的稳定性，但未对并网运行进行研究。文献[11]研究VSG 控制策略在自治和并网两种模式下的小信号模型，分析了VSG 控制参数对系统稳定性和动态响应性的影响。文献[12]将VSG应用于储能系统，并建立其小信号模型，总结得出VSG 关键参数整定方法。文献[13]通过对基于指数惯量的灵活VSG 控制技术进行小信号建模、灵敏度计算及根轨迹分析，得出主要控制参数对系统频率稳定性的影响规律，为控制参数的选择提供了依据。文献[14]提出一套完整的VSG 参数设计方法及其优化策略，通过应用控制变量法,分别改变阻尼系数、转动惯量、电压下垂系数和积分系数的值进行仿真和试验，验证了该方法具有较好的实用性。文献[15-16]研究了VSG 的小信号模型，利用根轨迹法对其进行稳定性分析，为VSG 参数设计提供理论依据。文献[17]提出基于储能型准Z 源逆变器的VSG 并网控制策略，不仅保留了准Z 源逆变器的优点还实现了频率的调节，大大提升了光储系统频率的稳定性。文献[18]将VSG 技术运用于混合储能的光伏并网系统中，实现了一次调频，提高了并网系统的稳定性。

针对采用固定参数VSG 控制技术，在负荷扰动下，频率调整不足，依然会导致系统不稳定，本文提出一种自适应转动惯量VSG 控制策略。为深入分析自适应转动惯量VSG 控制对微网频率稳定性作用机理，本文在常规VSG 的数学模型的基础上，利用同步发电机的功角特性曲线及转子角速度振荡周期曲线，分析了自适应转动惯量对微电网频率稳定作用机理，并对自适应转动惯量VSG 控制策略的稳定性分析及关键参数进行整定设计。最后，通过Matlab 仿真验证了该控制策略的有效性。

2 VSG 基本原理

VSG 控制策略由虚拟调速器、虚拟励磁控制器和双环控制器三部分组成，如图1 所示。

图中，L 为滤波电感，C 为滤波电容，P、Q分别为变流器输出的有功、无功功率；I 、U 分别为VSG 经LC 滤波后输出电流和电压。

(1) VSG 虚拟调速器的控制方程。

式中，J 为转动惯量；D 为阻尼；mP 、eP 分别为机械功率和电磁功率；ω、nω 分别为VSG、额定角速度；δ 为虚拟功角；m 为下垂系数；refP 为有功功率参考值； +1sτ 为低通滤波器。

(2) 虚拟励磁控制器。

式中，Q 表示输出的有功功率和无功功率；n 表示无功下垂系数；mU 为VSG 输出三相电压的有效值；ku为积分系数；Un为额定电压幅值； Qref为无功功率参考值。

由式(2)可得VSG 控制原理框图如图2 所示。

3 自适应转动惯量VSG 控制策略频率影响作用机理分析

结合同步发电机功角特性曲线和转子角速度振荡曲线，如图3～4 所示，进一步分析自适应转动惯量VSG 控制策略对频率影响作用机理。

[t1，t2]区间：在t1处减负载，ΔP 突然增加，对应于a 点向b 点运动。由转子运动方程及图4 可知，在t1瞬间，Δω 保持恒定，将导致J(dω/dt)急剧增大。因为J 为固定常数，所以dω/dt 增大。当达到t2时刻，Δω 增加至最大值，与此同时dω/dt 为零。在t1～t2区间，可以适当增大J，来限制dω/dt 的值，减少Δω 的最大值。

[t2，t3]区间：对应于由b 点到c 点，转子角速度仍然大于ωn，且dω/dt＜0，单调递减，即ω 减速向ωn靠近，此时应适当减少J，增大dω/dt，使得ω更快ωn向靠扰。

同理[t3，t4]和[t4，t5]区间分别类似于[t1，t2]、[t2，t3]区间。只有适当调整转动惯量才能使得系统频率响应特性更好。调整转动惯量规律如表1所示。

表1 转动惯量J 的选取原则

根据表1 选取原则，提出一种由角速度变化率和角速度变化量共同决定的自适应转动惯量其表达式为

式中，J0为VSG 稳态时的转动惯量；Δω 为角速度变化率；kj为转动惯量的调节系数。

4 稳定性分析及参数整定

4.1 稳定性分析

建立VSG 单机并网P-f 小信号模型对系统稳定性进行分析。VSG 单机并网等效电路图如图5 所示。

图5 中δ 为U 和 nU 的相角差，Z 为逆变器等效输出阻抗及线路阻抗之和，一般为感性。

同步发电机的功角方程

对eP 求导可得

则VSG 的转子方程可以改写为

由式(6)式可得

由式(7)可得VSG单机并网时小信号模型如图6所示。

根据式(7)，利用广义参数根轨迹法，对转动惯量J 进行稳定性分析影响，当D=20，m=20，J 取值0.01～15.00 的根轨迹图，如图7 所示。

由图7 可知，当D 和m 恒定时，J 越大，开环极点离原点越近，系统的稳定性逐渐变差，因此转动惯量不能取值过大。

4.2 参数整定

传统下垂控制P-f/Q-V 特性表达式

由式(8)可得

由式(9)可知，常规的VSG 转动惯量和阻尼系数为

将式(3)代入转子方程可得

将式(12)代入式(11)，自适应转动惯量表达式中不含角速度变化量的微分项，在算法实现上可以避免由于微分项引入的系统噪声干扰，更有利于系统的稳定。

对式(11)进一步简化可得

逆变器输出端等效输出功率为

由式(13)和(14)可得

忽略自适应转动惯量的正阻尼项，对式(15)线性化可得

式(16)是一个典型的二阶系统模型，由经典控制理论可知系统的自然振荡频率及阻尼比必须满足

由式(17)可得转动惯量 J0为

根据 ξ ∈[ 0 .1,0.8]、参数X 和阻尼系数D，求出转动惯量 0J 的取值范围为

稳态时，由式(20)可知

两种极端情况下，式(21)需要满足

系统稳态运行时，需要满足

由式(22)、(23)可得

则转动惯量调节系数jk 为

5 仿真分析

在Matlab 中搭建自适应转动惯量VSG 控制策略仿真模型，如图8 所示。表2 为给出的仿真参数列表。

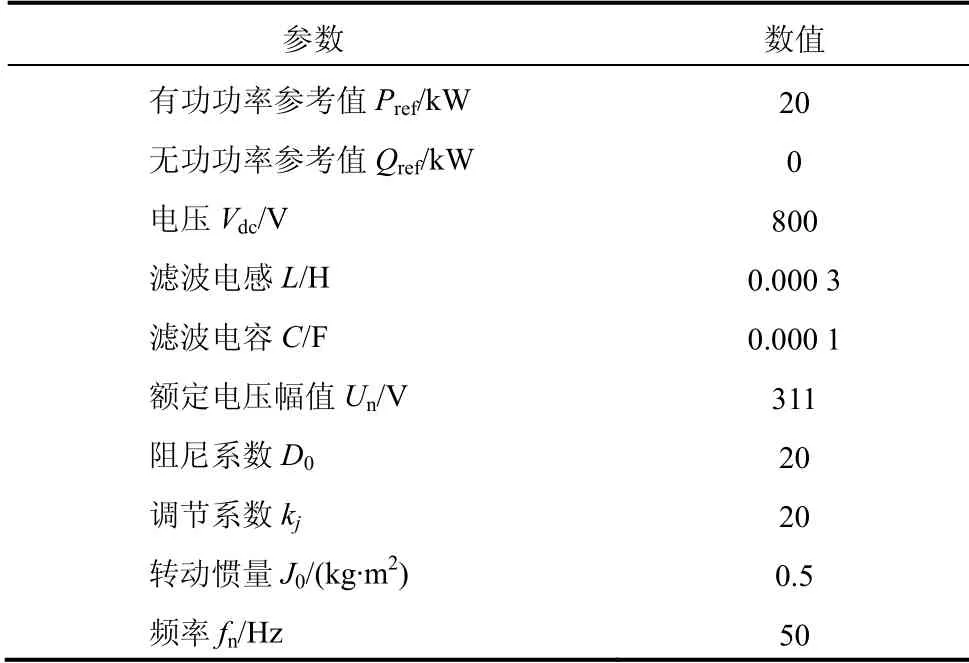
表2 仿真参数

(1) 孤岛运行时，设置t=0 s 时，系统负荷为10 kW；在t=0.4 s 时，系统加入10 kW 负荷；在t=0.7 s 时，再切除负荷。仿真波形如图9～11 所示。

由图9、10 可知，微网系统孤岛运行时，系统内部负荷发生变化时，自适应转动惯量使得系统频率幅度变化下降减少，保持系统的稳定性。而非自适应转动惯量的系统输出频率随负荷波动而变化幅度较大，系统频率的稳定性能更差。

(2) 并网运行，设置t=0 s 时，系统负荷为10 kW；在t=0.4 s 时，系统加入10 kW 负荷；在t=0.7 s 时，再切除负荷。仿真波形如图12～13 所示。

当微网系统并网运行时，由图11、12 可知，采用自适应转动惯量J 时，系统频率在负荷扰动时下降或上升的幅度明显减少。相对于采用固定转动惯量时，频率的稳定性得到提升。受外界负荷扰动时，自适应转动惯量使系统维持在50 Hz 与电网频率同步。

6 结论

为揭示自适应转动惯量虚拟同步机控制策略对微电网频率稳定性的作用机理，本文在常规VSG 的数学模型的基础上，研究了自适应转动惯量对微电网频率稳定作用机理，并对自适应转动惯量VSG 控制策略的稳定性分析及关键参数进行整定设计。进而提出自适应转动惯量VSG 控制策略，以提升系统频率和功率的稳定性。分别从离网运行和并网运行两种模式进行了仿真验证，通过对比分析可以得出以下结论。

(1) 在负荷扰动情况下，采用自适应转动惯量的VSG 控制策略系统的稳定性和动态性能较好。

(2) 相比常规的VSG 控制策略，采用自适应转动惯量VSG 控制策略系统的频率波动及输出功率的振荡明显得到抑制。

有关自适应转动惯量VSG 控制策略对频率的稳定性研究，可以结合自适应阻尼参数形成综合控制策略，进一步改进优化提升频率的稳定性和动态性。