测量不确定度在食品检验检测中的应用探究

（贺州市产品质量检验所，广西 贺州 542827）

食品检验检测在保障食品安全方面具有重要的作用，此项工作是由不同的测量项目组合而成，由于测量过程会受到多方面因素的影响，导致得出的结果与真值存在误差。为了有效地解决这一问题，可在食品检验检测的过程中，引入测量不确定度，保证测量结果的准确性。下面就测量不确定度在食品检验检测中的应用展开探究。

1 测量不确定度的原理及特点分析

1.1 基本原理

测量不确定度是一种能够对测量误差进行有效应对的方法。同时，还能对检验检测中应用方法理论的缺陷进行弥补，对整个实践过程具有指导作用。在检验检测过程中，检验人员的专业技术水平和操作能力均具有可提升的空间，随着水平和能力的不断提高，会使每次检验检测所得的结果及相关数据存在差异，需要指出的是，差异通常都是在允许范围内进行分散，这种分散性能够作为检验的参考依据。

1.2 主要特点

误差理论是开展数学研究中不可或缺的基础理论之一，对误差进行分析时，通常会运用到实验标准差，它是不确定度的重要理论依据，基于这一前提，可以认为测量不确定度是以误差理论为依托发展起来的，二者的分析与计算方法相同，只是在概念上存在区别。由于检验检测过程会受到诸多因素的影响，从而导致测量误差的出现，它是测量结果偏离真值的差值。

2 测量不确定度在食品检验检测中的应用

2.1 评定步骤

在测量不确定度的评定步骤中，数学模型的构建是一个较为重要的环节。在通常情况下，可以用相应的计算公式对被测量值进行表示，此时需要注意的一点是，在计算公式中，为了简化计算过程，将一些影响比较小的输入量忽略不计[2]。例如，在对标准溶液的浓度进行不确定度评定时，相关的计算公式为：

式中：C 表示溶液中物质的量浓度（单位：mol/L）。m 表示溶液中溶质的质量（单位：g）。M 表示溶液中溶质的摩尔质量（单位：g/mol）。

式（1）中并未对试剂本身的纯度P 加以考虑，这是因为P 的影响非常小，因此一般不会将其加入到计算公式中。为了确保不确定度评定结果的准确性及可信性，在构建数学模式时，应当将该因素考虑在内，由此所得的模型为C=mP/M。

2.2 不确定度的主要来源

在食品检验检测中，对测量不确定度进行应用时，所有可能对测量造成影响的因素，都会在一定程度上影响测量不确定度，所以，需要对不确定度的来源进行分析。

2.2.1 标准物质

国家现行的标准样品工作导则中，明确给出标准物质的定值原则及相关的统计方法。如果食品检验检测中，使用的标准物质本身存在误差，则会对不确定度评定造成影响，进而影响到检验检测结果的准确性[3]。

2.2.2 仪器设备

食品检验检测中需要使用天平进行称重，因不同型号的天平精度存在差异，由此产生的测量不确定度也会有所区别。精度为十万分之一的天平，其不确定度有2 个来源。1）示值。2）称量重复性。除了天平之外，还有分光光度计等仪器。

3 应用实例

为了验证测量不确定度在食品检验检测中的应用效果，以食品中的奶粉为例，将菌落总数作为检验对象，据此对测量不确定度进行评定。

3.1 奶粉菌落总数的检验检测方法

对奶粉样品进行称量，制作成相应倍数的稀释液，选取2～3 个稀释度的样品1.0 mL，分别加入到灭菌器皿中，并做空白对照，随后向每个器皿内加入适量的平板技术琼脂，放入恒温培养箱内进行培养，培养箱的温度控制在36℃±1℃，培养时间控制在48h±2h。将器皿从培养箱中取出，观察各个器皿内的菌落群数，做好相关记录，最后，对相同稀释度的器皿内试样的平均菌落总数进行求取，以此为依据出具检验检测报告。

3.2 检验检测中不确定度的来源分析

在奶粉检验检测中，对不确定度的来源进行分析前，需要先构建起奶粉菌落总数的数学模型，可将奶粉的菌落总数设定为A，用X 对检测结果进行表示，由此可得到如下数学模型：A=X CFU/g。在检验检测中，测量不确定度的主要来源如图1 所示。

图1 测量不确定来源示意图

3.2.1 样品的培养温度与时间

在该次检验检测中，样品为均一样品，实验过程为单一重复测试，鉴于此，样品培养阶段的温度基本上不会对测量不确定度造成影响，所以可将培养温度忽略不计。同理，培养时间也可忽略。

3.2.2 培养基

通过选用已知的菌种，对培养基的可用性进行验证，根据验证结果，在检验检测中选用统一培养基。

3.2.3 计量

通过对相关标准进行查询后得知，1 mL±0.007 mL 移液管的不确定度为0.0028 mL。同时，因菌落总数检测中称量并不需要细称，所以由此引起的不确定度可以忽略不计。

3.3 确定分量

该次检验检测是在某检测机构内进行的，是一次质量合格的测试。因此，可将测量不确定度的分量忽略。由于重复测量产生的不确定度在合成不确定度中的占比较大，所以需要对此予以重点考虑。不确定度的分量构成情况如图2 所示。

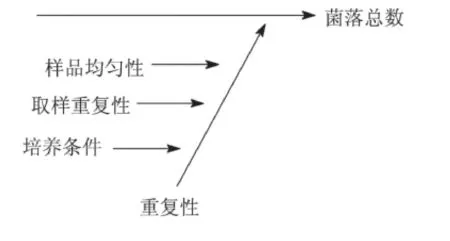
图2 不确定度的分量构成示意图

3.4 评定过程

在对奶粉样品的菌落总数进行测定时，由于需要重复测试，因此会得到多个不同的结果，并且这些结果之间存在一定的差异。对这些结果进行平均后，会产生不合理的偏差，且该偏差以102为单位，因此可用log 平均值，对测量结果进行表示[4]。该次检验检测所得的结果经log 处理后的平均值为2.7693（限于篇幅，计算过程省略）。

利用标准差公式，带入相关数值后，得到标准不确定度为0.02246，经查表得知，P 为95%时，扩展不确定度为0.0458。由此可得出奶粉菌落总数为2.7693±0.0458，取反对数值，可得出如下结论：该次检验检测中，奶粉的菌落总数在529～653 分布，引入测量不确定度后，奶粉的菌落总数在530～650 分布。据此可出具相应的检测报告，即该奶粉的菌落总数为（590±60）CFU/g，其不确定度为60 CFU/g。可见，测量不确定度在食品检验检测中具有良好的应用效果，能够显著提升测量结果的准确性。

4 结论

综上所述，食品检验检测是确保食品安全的重要工作，在此项工作的开展中，可以对测量不确定度进行合理应用，由此能够进一步提升食品检验检测结果的准确性。在具体应用时，要根据检验检测对象，构建起相应的数学模型，并对不确定度的来源进行分析，确定相关分量，最终完成不确定度评定，出具报告。