基于故障树的永磁直驱风力发电机组故障分析
2020-04-30
(1.湘电风能有限公司, 湖南 湘潭 411101;2.海上风力发电技术与检测国家重点实验室(湘潭电机股份有限公司),湖南 湘潭 411101)
0 引言
随着全球化石能源的紧缺,大力发展可再生能源已经成为世界各国的共同目标,其中风力发电作为可再生的清洁能源之一,技术日趋成熟,具有商业化发展的可能性,能够在全世界范围内进行大规模的推广[1]。
作为一个大型复杂的机电系统,对风力发电机组的可靠性进行研究不是易事,仅从设计角度出发,正向分析风力发电机组的可靠性不仅困难,而且也可能不符合风力发电机组的实际运行状况。因此,该文针风电场的实际运行情况,利用其运行过程中产生的数据,结合相关的可靠性方法,对风力发电机组进行运行故障分析,并提出切实可行的维修措施,以此来缩短风力发电机组的维修时间,提高风力发电机组的维修效率,进而提升风力发电机组的发电量,提高风场的运营效率[2]。
1 永磁直驱风力发电机组的基本结构及运行数据统计
1.1 永磁直驱风力发电机组的基本结构
该文研究的风场安装的风力发动机组(以下简称风机)为水平轴永磁直驱风机,发电机采用多极电机与叶轮直接连接进行驱动的方式,免去齿轮箱这一传统部件。其具有发电效率高、运行及维护成本低等特点,但对发电机的要求很高,发电机的结构复杂且体积庞大,不方便吊装[3]。
风机作为复杂的机电一体化系统,其组成部分主要分为机械和电气2 类,涉及的具体部件及元器件繁多,主要包括叶片、轮毂、回转支撑轴承、发电机、机舱、塔筒、变流器、偏航系统、制动系统和变桨系统等[4]。为了简化分析,将风机运行时产生的相关故障进行归类处理,结合风机自身的结构特点,将风机系统分为6 个部分,即叶片、轮毂、机舱、偏航、塔筒及变流器,图1 为直驱型风机结构的关系示意图。
1.2 目标风机的故障数据处理
由于风机运行时容易受外界环境的影响,因此选择具有代表性风电场的风机进行分析,这样不仅能够更加准确地分析出风机自身的可靠性,而且分析结果也具有代表性,能够对相关风场的风机运维提供指导性建议。该文选择的风场位于南方某中部省份,是一个的典型的南方山地风场,其地形特点和气候条件都具有代表性,对其进行分析能够起到举一反三的效果。选择的风场共有24 台机组,统计时间为365 d,经过对运行数据的处理,得知24 台风机在统计时间段的故障次数及累计故障停机时间,见表1。
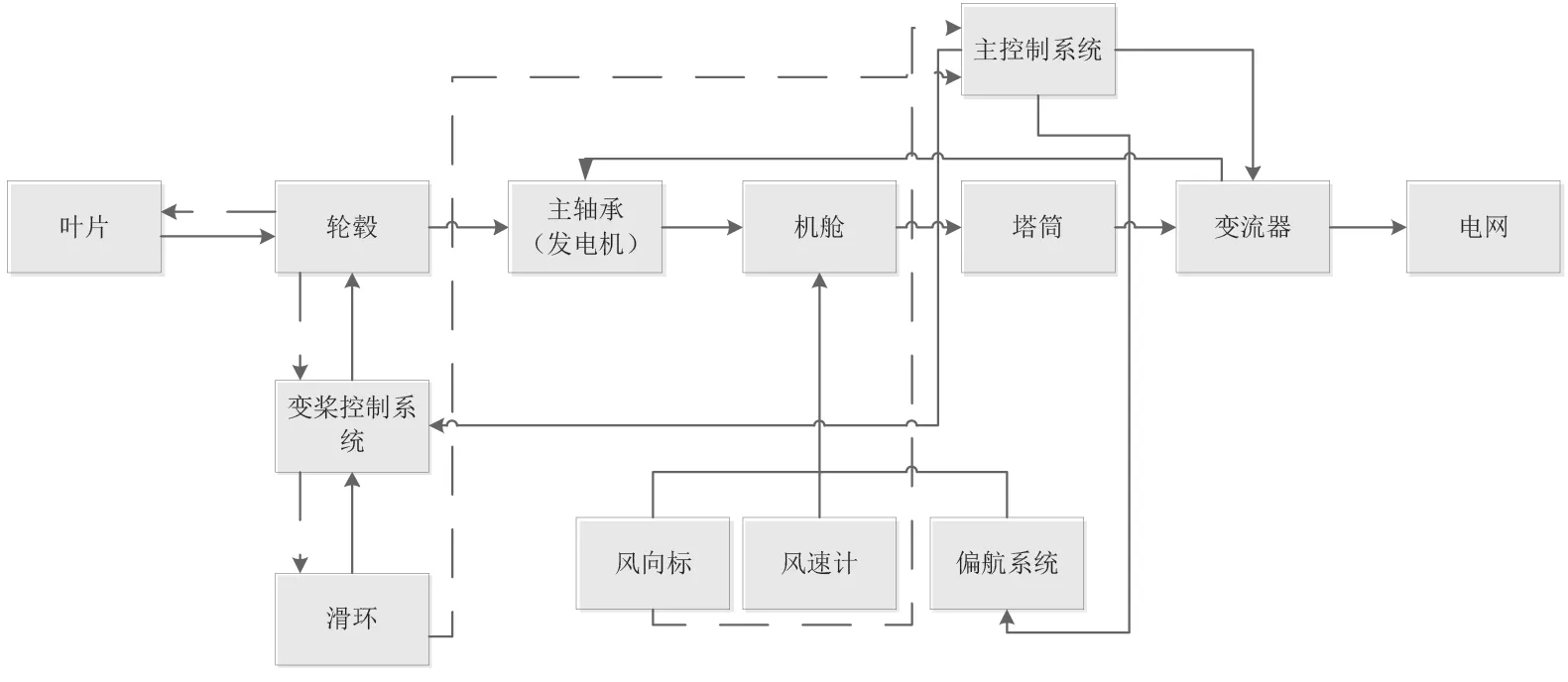
图1 风机结构关系示意图

表1 24 台风机统计周期内故障次数
已知风机在统计周期内的故障次数和累计停机时间,结合风场的风机在统计周期内发生的基本故障,可以求出风机发生的每一个基本故障的平均故障修复事件(MTTR)和平均故障前时间(MTTF)。为了消除偶然性,真实客观地反应出风机的运行性能,对整个风场所有风机发生的某一个故障求取MTTR和MTTF,风场统计周期内发生故障的类别及其MTTR 和MTTF占比前10 的故障事件,见表2。
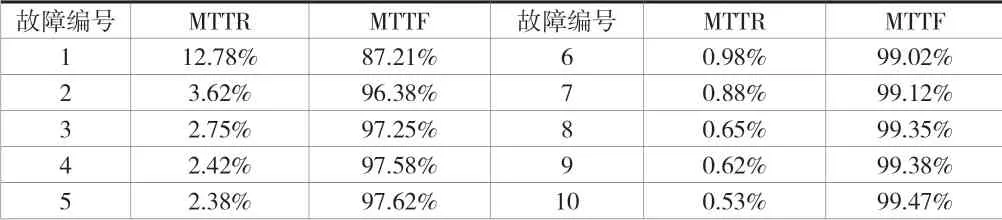
表2 风机基本故障事件MTTR 和MTTF 占比
2 大型永磁直驱风力发电机组故障分析方法
2.1 基于故障树的可靠性分析
故障树分析方法(FTA)是自上而下的演绎式失效分析法,利用布林逻辑组合低阶事件,分析系统中不希望出现的事件或者状态[6]。进行故障树定性和定量分析时,需要做出2 个假设。1)故障树各底事件之间相互独立。2)底事件和顶事件都只有2 种状态,即正常或故障。
在得到顶事件的最小割集之后,顶事件发生的概率可以通过最小割集计算:系统的所有最小割集为K1,K2,…,Ki,…,Kj,…,Kj,…,Kk,…,KR,其中i,j,k 为1 至R 中任意数字且1 ≤i<j<k ≤R,R 为最小割集的个数,最小割集发生的概率为P(K),P(Ki)表示的是第i 个底事件发生的概率,则顶事件T发生的概率P(T)(不可靠度Fs(t))发生的概率为:

式中:R 为最小割集的个数。
当各个最小割集中没有重复出现的底事件时,公式(1)可以变化为:

由公式(2)可知,此时顶事件的发生概率等于所有最小割集的发生概率之和,而最小割集的发生概率由其所包含的底事件发生概率相乘得到。当最小割集彼此具有的底事件有一部分相同时,顶事件的发生概率为:

在故障树分析中,不仅需要关注最小割集和顶事件的发生概率,还需要分析底层事件对于顶层事件的重要度,底事件或者最小割集对顶事件的发生的贡献定义就是其重要度。通常情况下,各个底事件或最小割集不是同等重要的,有的底层事件发生必然导致顶事件发生,有的则不然。因此,正确分析底事件对顶事件发生的重要度,对于确定系统薄弱环节及改进设计方案具有重大的意义。结合风机运行和故障维修的特点,选择关键重要度进行底事件或最小割集重要度的计算。
故障树的关键重要度Ic(i)指的是故障树第i 个底事件发生概率的相对变化,导致顶事件发生概率变化的相对变化率,其公式为:

i=1,2,…n,n 为底事件个数
式中:qi为底事件发生的概率,为故障树的故障概率函数, 为求导数。
2.2 风力发电机组故障树分析
根据风机实际运行情况,结合上文收集的数据,利用故障树分析法对风机在运行过程中因故障导致的停机问题进行分析,以风机故障停机为顶事件,结合风机的结构特点,将风机FTA 的模块划分为变桨、偏航、控制、变流器系统和其他部分组成[7-8],在该基础上,根据风机各个组成系统的特点再进行更底层次的划分,直至划分至底事件为止,各个系统底层划分如图2 所示。
将表2 中风机在统计周期内发生的基本故障事件的相关故障数据信息导入后,可得到故障树的定量分析结果,如图3所示。由图3 可知顶事件发生概率(不可用度)为0.02184,则其可用度为0.97816,在风机的运行过程中,MTTF 为0.1 年,即36.5 天,在风机的全寿命期间总停工时间为0.4367 年(总寿命为20 年)即接近160 天,GT1、GT2、GT3 和GT14 分别代表控制系统、偏航系统、变桨系统和变流器系统,其重要度分别为0.2957、0.008997、0.6663 和0.02901,这说明变桨系统对于风机的重要度较其他系统更高,符合风机的实际运行规律。求取故障树的最小割集和最小割集的关键重要度,见表3(列出重要度前10 的最小割集)。

表3 最小割集及关键重要度
通过分析故障树的最小割集及其关键重要度可知,基本故障事件6、12、1 和8 的关键重要度最大,这说明顶事件对这4 个基本故障事件的故障发生概率比较敏感,提高这4 个基本故障事件的可靠性,能够显著降低顶事件的发生概率,进而提高风机的可靠性。
3 结论

图2 风机故障停机故障树
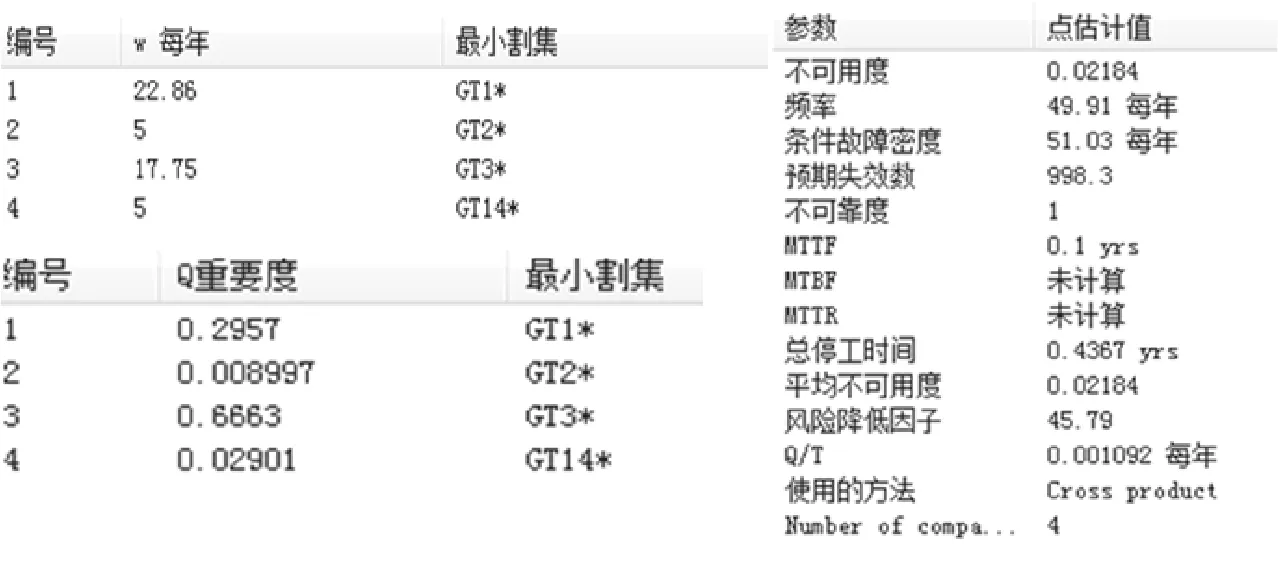
图3 故障树分析结果
该文以某型永磁直驱发电机组为例,结合该型号风机运行过程中产生的故障事件数据,基于故障树可靠性分析方法对其进行可靠性分析,建立以风机故障停机为顶事件的故障树模型,并将故障事件数据代入模型中,进行定性和定量分析,得出影响风机故障停机发生概率主要的基本故障事件,风机在维修期间应该重点修复该类事件,提高其可靠性,从而降低风机故障停机的发生概率,提高风机的可靠性,同时也为后续机型设计过程中的可靠性分析和优化提供了切入点。
