基于三通道2D-CNN的逆变器功率管开路故障诊断方法
2020-04-30
(1.武汉理工大学 能源与动力工程学院,武汉 430063;2.中国船舶重工集团第七一一研究所,上海 200000)
变频器是船舶电力推进系统中的核心设备。有资料统计表明,变频器中主电路的开关装置失效所引起的故障约占变频器故障的80%[1]。开路故障是开关装置的典型故障形式,精确找到开关装置的开路故障点可极大程度地缩短检修时间。关于变频器开路故障诊断的方法大多可分为基于模型[2]和基于数据驱动[3-6]两种方法。基于模型的方法必须分析电力系统中的电气物理过程和组件之间的相互作用,在实际应用过程中很难建立精确的数学模型表达式,因此,大多研究采用基于数据驱动的机器学习算法来解决该问题。常见的机器学习算法主要有支持向量机(SVM)、K-最近邻(KNN)和深度神经网络(DNN)。这些方法在变频器故障诊断领域应用较为广泛且技术相对成熟。但是,上述方法存在学习能力差、需要复杂的人工特征提取过程、易引起模型过拟合等问题,难以满足变频器故障诊断的精度要求。因此,卷积神经网络被越来越多的引入故障诊断领域[7]。本文拟采用卷积神经网络来解决三相电压源型逆变器功率管开路故障诊断精度较低问题。
1 诊断模型的理论基础
1.1 卷积神经网络
卷积神经网络在识别任务方面有优异的性能。一般来说,每层神经网络包括两部分:卷积层和池化层,一个常规的卷积神经网络模型是通过叠加一层或多层神经网络,外加一个分类层,见图1。

图1 卷积神经网络结构
1.1.1 卷积层
卷积层是CNN模型的核心构件。通过卷积核对输入图片进行特征提取,然后利用激活函数生成特征图,通常为RELU函数。过滤器使用相同的内核,即权重共享。Wi和bi分别用来表示第i层Li的权重和偏置,Li-1用来表示第(i-1)层特征图。卷积过程定义如下:
Li=f(Wi⊗Li-1+bi)
(1)
f(·)是非线性的激活函数。利用RELU函数作为模型的激活函数,加速CNN模型收敛。
1.1.2 池化层
卷积层后的池化层也称为分样层,层的功能是减少模型中的参数和计算量。
(2)
式中:Pi(k)为i层中的第k像素值,k∈[(j-1)W+1,jW];W为池区域的大小。
1.1.3 softmax分类器
softmax函数为
(3)
当输入数据集有m样本时,CNN模型的损失函数为交叉熵函数。
(4)
式中:I{·}为指标函数,如果y(i)等于J则返回1,如果不等于则返回0。通过在训练过程中将损失函数J(θ)最小化,对参数进行更新。
1.1.4 优化算法
所用Adam学习算法不再更新所有训练数据集的权重,而是更新一小批训练数据集的权重,可在满足权重更新的基础上极大程度地减轻计算负担。
过去梯度的衰变平均值mt和过去平方梯度的衰变平均值vt计算如下。
(5)
式中:β1=0.9,β2=0.999(参数β1、β2取值接近1时,估计值偏差接近0)。
1.2 过拟合问题的解决方法
模型训练优化参数时,为了避免CNN模型的过度拟合,采用Dropout和自适应学习速率的学习技巧[8]。
Dropout在训练过程中,随机的丢弃一部分输入,丢弃率通常为0.5,此时丢弃部分对应的参数不会更新,通过随机丢弃可以得到各种子网络,然后将所有子网络结果进行合并[9]。假设有l层隐藏的神经网络,用d(l)和y(l)表示输入和输出的向量,用w(l)和b(l)表示第l层的权重和偏差,正常神经网络的前馈计算(见图2a))定义如下。

(6)
式中:f(·)为激活函数,f(x)=1/(1+exp(-x))。
加入Dropout的神经网络前馈操作(图2b))。
(7)
式中:s(l)为具有概率p的伯努利随机变量的向量。
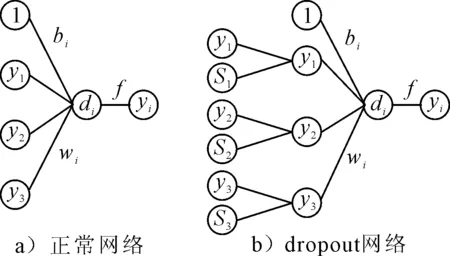
图2 正常网络与加入Dropout网络对比
学习速率参数的设置对模型精度有很大的影响。不适当的学习速度会降低神经网络模型的性能。针对这一问题,提出一种自适应学习速率法,根据训练迭代次数调整学习速度。学习速率lr设定为

(8)
式中:n为迭代次数;niter为迭代次数的设定值。
2 逆变器开路故障仿真模型
2.1 模型搭建
通过Matlab/Simulink建立三相电压源型逆变器的仿真模型。三相电压源型逆变器由3个单相半桥的DC-AC拓扑组成,三相拓扑以120°的交联方式工作,核心器件是I1~I6 6个IGBT功率管,负载为三相永磁同步电动机。仿真模型见图3。所需数据从Scope Iabc获得,模型中相关参数设置见表1。

图3 三相电压源型逆变器仿真模型
2.2 故障模拟
分析三相电压源型逆变器可能出现的开路故障,选择单管开路故障为诊断目标,加上无故障情况,7种状态见表2。
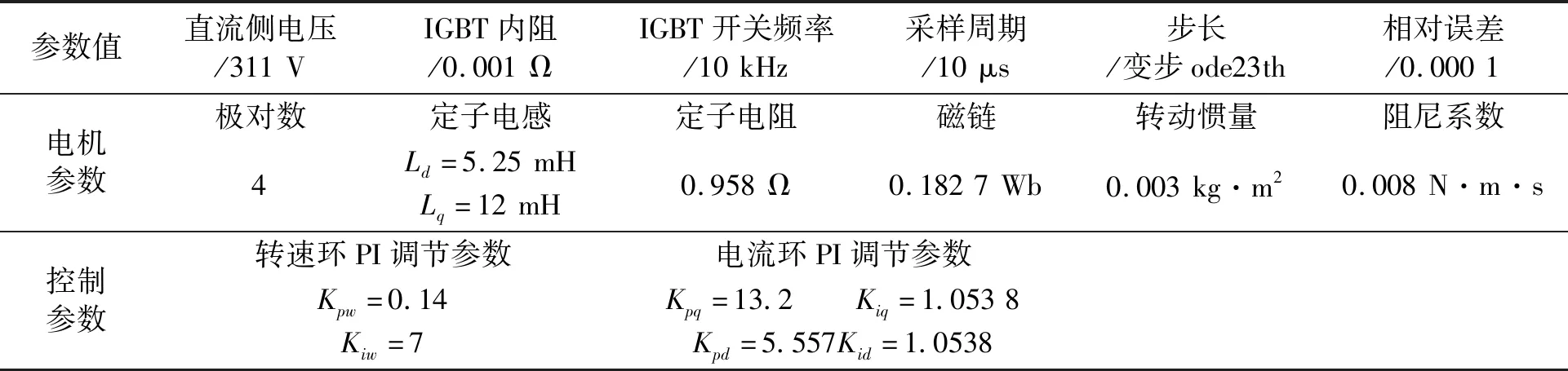
表1 仿真模型参数

表2 故障类别标签设置
3 故障诊断过程
故障诊断过程见图4。
首先从仿真模型中的Scope Iabc以24 kHz的频率采集数据为7种不同状态分别收集864 000组数据,每组数据包括a、b、c三相电流值。然后对数据进行预处理,按照下式对数据进行归一化处理。
考虑三相电流值作为3个指标,构建输入格式为三通道的CNN模型。经过反复尝试,样本数据被划分为12 600个格式为(480,3)的样本,即每个样本包括480组三相电流值,样本数据(480,3)被重塑成维度为(24,20,3)的样本数据集,见图5。
(9)

图4 故障诊断过程

图5 数据重塑过程
数据集被随机分为3个子集,包括训练数据集、验证数据集和测试数据集,将三者比例分别设置为65%、15%和20%。训练数据集用于训练故障诊断方法。验证数据集是为了防止训练过程中过度拟合,当验证数据集错误增加时中断训练过程。测试数据集用于评估诊断模型的性能。
最后,构建CNN模型,将预处理后的数据集输入到该模型中进行训练及测试。采用CNN模型参数,通道数设为3,不同通道采用相同的结构参数见表3,诊断结果见图6。
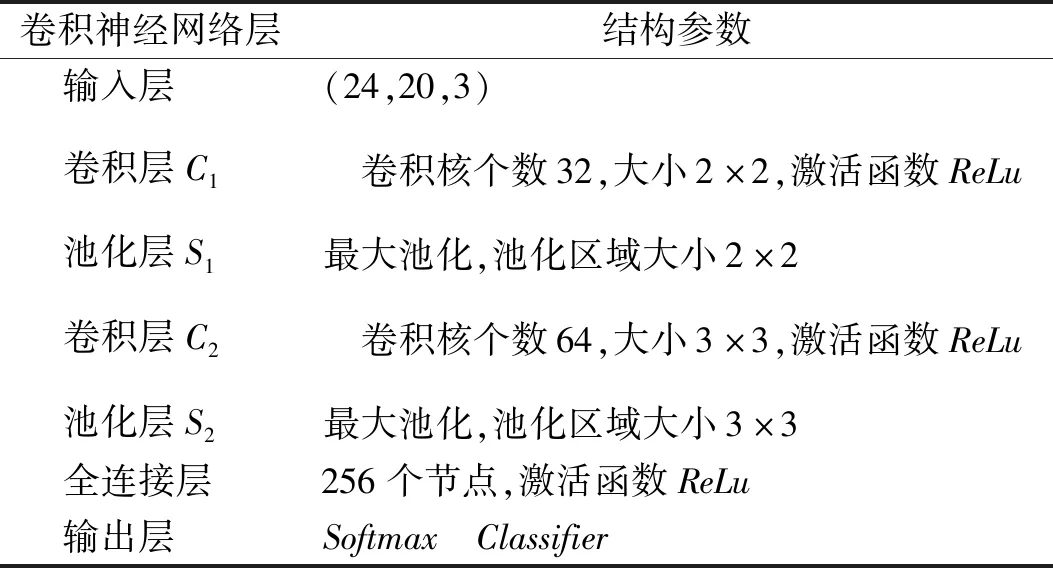
表3 CNN模型参数
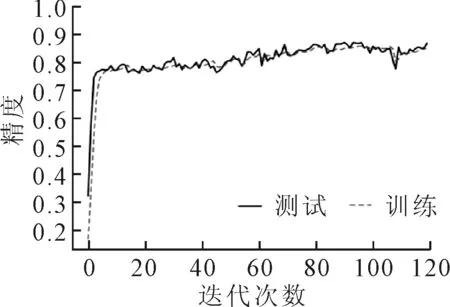
图6 三通道CNN模型训练结果
训练后的三通道CNN模型诊断精度可达99.66%,召回率可达99.66%。
4 不同诊断方法的性能比较
4.1 单通道2D-CNN模型
使用与三通道2D-CNN模型相同的原始数据,在归一化处理后将18 144 000个数据划分成37 800个维度为(24,20,1)的样本。将通道数设为1,除输入层结构与三通道CNN模型不同,其他参数不变。训练后的单通道CNN模型诊断精度仅达到91.52%,召回率89.63%,训练结果见图7。单通道CNN模型相比于三通道CNN模型诊断结果相差很大,说明三通道结构的数据输入格式更易于CNN模型挖掘本文数据结构的特征。
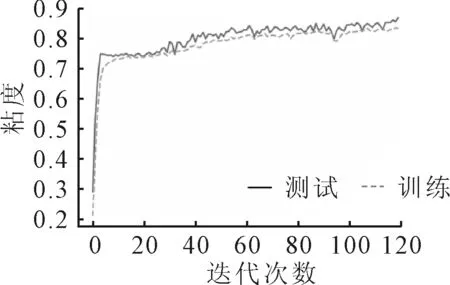
图7 单通道CNN模型训练结果
4.2 传统数据驱动方法及DNN
在传统的故障识别算法中,多采用特征工程方法。本文收集文献中所使用的统计特征,即表4中频率的4个特征和时间域的10个特征。每种状态的数据被划分成5 400个大小为480的样本,计算得到每个样本的14种特征,共计5 400×14×7条特征数据并作为KNN和SVM模型的训练数据集。
此外,DNN也被用来与所提出的方法进行比较,用于比较的DNN模型有5个神经网络层(输入层,3个隐藏层,输出层),使用相同数据预处理方法及深度学习技巧。

表4 在时间和频率域中选择的特性
不同方法比较结果见表5。本文所提方法与KNN和SVM相比,精度分别提高了29.85%和30.9%,召回率分别提高了31.91%和58.8%。与DNN诊断结果相比,提高了2.1%、2.54%。

表5 不同方法结果对比 %
5 结论
1)所提出的诊断方法相对于DNN、KNN及SVM等常用方法,数据处理过程简单,自主学习能力强,能够有效提高逆变器功率管开路的故障诊断精度。
2)在数据预处理时将三相电流数据值划分为3个维度的输入格式可提高模型的学习能力。
3)只考虑了单管开路故障,逆变器还存在双管开路等更多复杂故障类别,后续将使用该方法做进一步研究。
