结合KNN和图标签传播的密度峰值聚类算法
2020-04-29吴辰文蒋雨璠马宁
吴辰文 蒋雨璠 马宁


摘要:密度峰值聚类算法(DPC)是一种基于密度的高效聚类算法,该算法指定参数少、聚类速度快、能发现非球形簇状等优点,但传统DPC算法截断距离参数的选取需要人工干预,且剩余数据点的标签分配易受“多米诺”连锁效应影响。针对这些问题,提出了结合KNN和图标签传播的密度峰值聚类算法(DPC-NNLP),该方法在KNN思想的基础上来计算各样本数据点的局部密度值,通过KNN算法形成的最近邻点构造局部密度主干区域,并运用基于密度的KNN图将标签分配给剩余的点以形成最终的簇。该算法考虑了各数据点间的相关性,可以有效地对各种形状和密度差异性较大的数据进行聚类。在多个数据集上进行了实验仿真,经过对比验证,该文提出的密度峰值聚类算法在多数情况下聚类效果要优于其他的算法。
关键词:数据聚类;密度峰值;KNN算法;标签传播
中图分类号:TP301.6
DOI:10.16152/j.cnki.xdxbzr.2020-06-014
Density peak clustering algorithm combinedwith KNN and label propagation
WU Chenwen, JIANG Yufan, MA Ning
(School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
Abstract: The density peak clustering algorithm (clustering by fast search and find of density peaks, DPC) is an efficient density-based clustering algorithm, which owns the advantages of less specific parameters, fast clustering speed, and can find non-spherical clusters. However, all the traditional DPC algorithms have the defects that the selection of truncated distance parameters needs manual intervention, and the label allocation of the remaining data points is vulnerable to the "Domino" linkage effect and so on. To solve these problems, a density peak clustering algorithm (density peak clustering algorithm combined with KNN and label propagation, DPC-NNLP) that combines KNN and graph label propagation is proposed. This method calculates the local density values of each sample data point on the basis of the idea. The local density backbone region is constructed by the nearest neighbor points formed by the KNN algorithm. The label is assigned to the remaining points to form the final cluster by using the density-based KNN graph. This algorithm considers the correlation between the data points and can effectively cluster the data with different shapes and densities. Experimental simulation is carried out on multiple data sets. The results show that the density peak clustering algorithm is better than other algorithms in most cases.
Key words: data clustering; density peak; KNN algorithm; label propagation
聚類算法作为数据挖掘技术的一项重要的技术手段, 应用十分广泛。 因其算法无需任何先验知识, 即可将数据组织、 聚集为多个组, 且各组组内具有相同特性、 组间又具有不同特性。 由于其特有的优势及高效的计算能力, 现在已成功运用在多个系统领域, 如生物信息学[1-2]、 工业发展[3]、 网络安全[4]、 图像处理[5]、 医学诊断[6]等。
到目前为止,已经有多种聚类算法被提出,其中在2014年Rodriguez和Laiozai在Science上提出的一种基于密度的聚类算法(clustering by fast search and find of density peaks,DPC)[7],由于该算法具有原理简单、能够快速发现任意形状的簇、且无需迭代的优点,在近几年一直是热门研究课题。虽然密度峰值聚类算法具有很多的优点,但该算法的缺点也很突出。DPC算法主要存在以下几个方面的不足:①算法中一项重要参数截断距离的取值难以确定,一般主要依靠人工进行选取,缺乏客观的选择依据;②聚类中心的选取也依靠主观经验人为干预,导致主观性较强,且聚类结果的准确性得不到保障;③在算法识别出数据的密度峰值点后,即将每个剩余点分配给密度较高且相近的点,这样的分配策略会导致数据点一旦错误分配后误差的传播,产生“多米诺效应”。
基于上述背景,本文提出了结合KNN和图标签传播的密度峰值聚类算法(density peak clustering algorithm combined with KNN and label propagation,DPC-NNLP),算法主要结合K最近邻算法[8](K-nearest neighbor, KNN)加以图标签传播的聚类算法,旨在解决上述所提到的DPC算法的相关缺陷与不足,通过KNN算法构建数据样本间的联系,形成数据点之间的邻居网络,提高结点间的关联性,准确计算各数据点的局部密度,并通过使用图标签传播进行剩余点的精准分配形成最终的簇。
1 相关工作
近年来将K近邻的思想引入到DPC算法中是一个研究重心,在2015年Lan[9]等人开发了一种基于查找密度峰值的新算法,以优化K均值的初始中心证明DPC算法是用于选择初始中心的一种有价值的方法;2016年谢娟英[10]等人为了克服传统DPC算法中样本局部密度定义及在分配策略中的缺陷,提出了一种K近邻优化密度峰值聚类算法,该算法在DPC中引入了K近邻的思想,利用数据样本点的K近邻信息定义样本的局部密度进行样本密度峰值的搜索;同年,Du[11]等人为了克服传统DPC算法未考虑数据的局部结构的问题,提出了一种K最近邻的密度峰值聚类算法,该算法在DPC中引入了K最近邻的思想,并在此基础上引入了主成分分析实现了对高维数据的准确聚类,增强了算法精度;2017年Yao[12]等人提出了一种自适应聚类算法,引入K最近邻的思想来计算截断距离参数和局部密度,算法仅需要一个参数,整体的聚类过程避免了主观因素;2018年杜沛[13]等人提出了一种基于K近邻的比较密度峰值聚类算法,该算法重新定义了截断距离和样本局部密度的度量方式,改进后的计算方式更贴合数据的真实分布,在准确率上得到有效提高。大部分論文均应用截断距离参数来进行密度估计,对此,本文采用文献[11]引入的局部密度度量方法来进行密度的计算,该方法可以有效、准确地识别聚类中心。
同时, 针对于密度峰值聚类算法的密度度量标准也是各研究学者的重心, 在2017年Ding[14]等人提出了一种基于模糊熵概念的密度峰聚类算法, 针对数据类别或数值相关属性, 提出了一种新的相似性度量标准, 并且为了避免分类和数值之间的特征转换和参数调整, 提出了一种新的相似性度量, 以重新定义数据点的局部密度, 提高了算法的鲁棒性;同年, 王飞[15]等人针对于DPC算法大型数据集有效聚类的问题, 提出了一种基于网格的新算法, 称为基于网格的密度峰值聚类算法。 在计算局部密度时, 引入网格划分的思想以减少算法的计算量, 有效地解决了算法运行效率问题。
2 结合KNN和图标签传播的密度峰值聚类
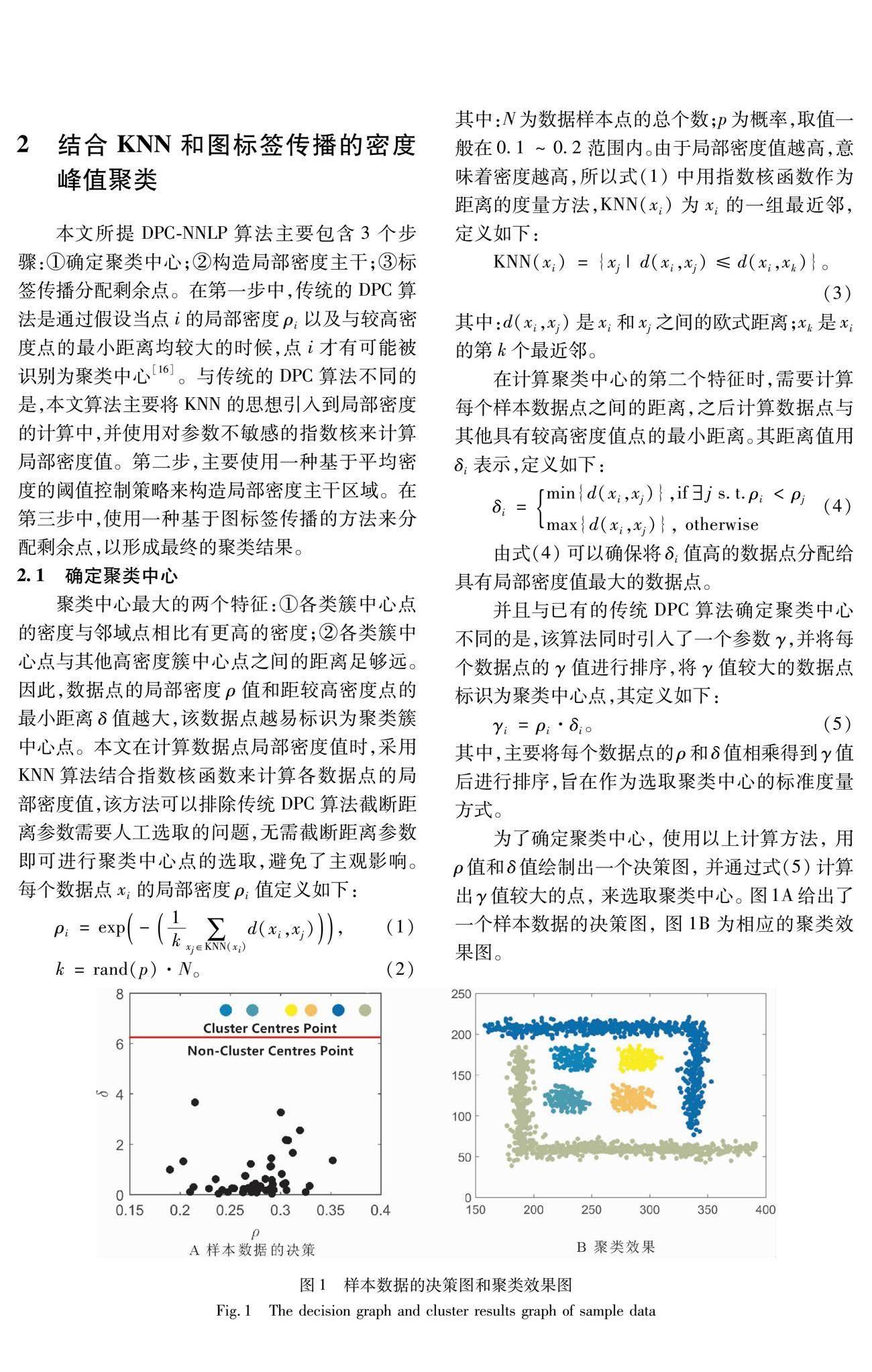
本文所提DPC-NNLP算法主要包含3个步骤:①确定聚类中心;②构造局部密度主干;③标签传播分配剩余点。在第一步中,传统的DPC算法是通过假设当点i的局部密度ρi以及与较高密度点的最小距离均较大的时候,点i才有可能被识别为聚类中心[16]。与传统的DPC算法不同的是,本文算法主要将KNN的思想引入到局部密度的计算中,并使用对参数不敏感的指数核来计算局部密度值。第二步,主要使用一种基于平均密度的阈值控制策略来构造局部密度主干区域。在第三步中,使用一种基于图标签传播的方法来分配剩余点,以形成最终的聚类结果。
3 实验与分析
本文仿真实验所使用的计算硬件配置为Intel Core i7-9750H处理器、 16GB内存; 实验的软件环境为Windows 10 64bit操作系统, 采用Matlab R2018a编程环境。
将本文提出的DPC-NNLP算法与相关的聚类方法进行了对比,这些算法包括:标准DPC算法、DBSCAN算法和IDPC算法[20]。所用到的数据集主要包括D31,R15,Flame和Aggregation 4个人工数据集以及Spectf Heart,Abalone,Wine 3个实际数据集,数据集属性如表1所示。其中,R15,Aggregation和D31均为二维数据集,D31和Abalone数据集样本数量较多,Spectf Heart,Abalone和Wine均为多维数据集。
3.1 评价指标
为了对比聚类结果,本文使用几种著名的评价指标来评价各种聚类算法的性能,这些评价指标包括调整Rand系数[21](adjusted rand index,ARI)和调整互信息指标[22](adjusted mutual information, AMI)。
Rand系数[23](rand index, RI)和调整Rand系数都经常作为聚类模型的评价指标。假设C为实际类别信息,K为聚类结果,则RI系数的定义如下:
RI=a+bCn2 。(8)
其中:a表示在C和K中都属于同一类别的点对数,b表示在C和K中都不属于同一类别的点对数;n代表数据样本点的总个数,由于Rand系数的取值范围只在[0,1]之间,当聚类结果完美匹配时RI的值为1。为了使RI系数具有更高的区分度,本文运用了ARI系数。定义如下:
ARI=RI-E(RI)max(RI)-E(RI)。(9)
其中:ARI的取值范围为[-1,1],当ARI的值趋近于1的时候,聚类结果越接近数据集的原始标签。
AMI指标是基于互信息MI(mutual information based scores)的一个概念,同时也是评价聚类方法的一个著名且广泛使用的指标,通过给定的聚类效果使用信息论来量化其数据集真实标签之间的差异,估计聚类的质量,其定义如下:
AMI=MI-E(MI)max(H(A),H(B)-E(MI)), (10)
MI(A,B)=∑i∈A,j∈Bp(i,j)logp(i,j)p(i)p(j)。 (11)
其中,A和B分別为同一个数据集使用两种不同聚类方法得到的类别标签,AMI的取值范围为[-1,1],E(MI)为MI的数学期望,在当AMI的值趋近于1的时候,聚类效果越好,若完全不同的情况下,AMI值等于-1。
3.2 聚类结果与分析
将本文所提DPC-NNLP算法及DBSCAN、DPC、IDPC 3种算法在4个数据集上进行了聚类效果可视化,其中包括Aggregation,D31,Flame以及Wine数据集,效果如图3所示。对于Aggregation和Flame两个二维数据集,由于其类簇间隔较大,样本的数据量较少,聚类相对简单,对于二维的D31数据集,由于各簇之间的间隔较紧密,数据集的数据量较大,易出现错误聚类的情况。但通过图3可以看出,对于D31数据集,本文所提出的DPC-NNLP算法的效果均优于其他3种算法。
各算法所使用的AMI及ARI指标如表3所示。图4和图5分别表示了AMI和ARI指标的对比情况。
在Wine数据集中共有3个类簇,除了一个密度相对较大的簇,其余两个类簇的样本点分布均比较分散,样本数据点间的密度比较接近,对于DBSCAN算法由于其算法自身的缺陷出现了数据点错误聚类的情况。同时,由于传统DPC算法比较容易形成多个类簇中心,进而影响对Wine数据集的聚类效果。但从图3可以看出DPC-NNLP算法对于Wine数据集的聚类较明显,可以准确选出正确的类簇中心点,聚类效果明显优于其他算法。对于维度较高的Spectf Heart数据集,DPC-NNLP算法聚类效果略有下降,同时DPC算法以及DBSCAN算法出现了明显的下滑,该算法还是明显优于其余3种算法。
本文提出的DPC-NNLP算法具备对初始参数并不敏感、剩余点的分配较为准确的特性,而其余算法在其运行过程中,总会有部分参数需要人工进行干预选取,所以会出现聚类效果低于本文提出算法的情况。因此,DPC-NNLP算法在聚类质量上相较于其他同类算法明显提升。
4 结语
本文主要针对密度峰值聚类算法中无法自动确定截断距离参数的问题,以及算法在剩余数据点标签分配时的缺陷,提出了一种结合KNN和图标签传播的密度峰值聚类算法,该算法通过结合KNN算法并运用KNN图来改进密度峰值聚类算法。通过采用DPC-NNLP、IDPC、DPC和DBSCAN算法分别对UCI数据集及人工数据集进行实验验证,并对实验结果进行对比分析,结果表明本文提出的结合KNN和图标签传播的聚类算法明显优于IDPC、DPC和DBSCAN算法,该算法可以更加准确的发现聚类中心点,将非聚类中心点精准、快速地分配到相应的类簇,对结构复杂的大规模数据处理性能更好,下一步的研究目标是如何剔除噪声点及异常点的检测。
参考文献:
[1] WEI D, JIANG Q S, WEI Y J, et al. A novel hierarchical clustering algorithm for gene sequences[J]. BMC Bioinformatics, 2012, 13:174.
[2] WANG F, ZHOU J Y, TIAN Y, et al. Intradialytic blood pressure pattern recognition based on density peak clustering[J]. Journal of Biomedical Informatics, 2018, 83: 33-39.
[3] 程启明, 张强, 程尹曼,等. 基于密度峰值层次聚类的短期光伏功率预测模型[J]. 高电压技术, 2017, 43(4): 1214-1222.
CHENG Q M, ZHANG Q, CHENG Y M, et al. A short-term photovoltaic power prediction model based on density peak hierarchy clustering[J].High Voltage Techology,2017,43(4):1214-1222.
[4] LI T,WANG J W. Research on network intrusion detection systembasedonimproved K-means clustering algorithm[C]∥2009 International Forum on Computer Science-Technology and Applications. IEEE, 2009:76-79.
[5] SULAIMAN S N, ISA N A M. Adaptive fuzzy-K-means clustering algorithm for image segmentation[J].IEEE Transactions on Consumer Electronics, 2010, 56(4): 2661-2668.
[6] 张宜, 谢娟英, 李静, 等. 红斑鳞状皮肤病的聚类分析[J].济南大学学报(自然科学版), 2017,31(3):181-187.
ZHANG Y, XIE J Y, LI J, et al. Clustering analysis of erythematous scaly skin diseases [J].Journal of Jinan University: Natural Science Edition,2017,31(3):181-187.
[7] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J].Science, 2014, 344(6191): 1492-1496.
[8] LAAKSONEN J, OJA E. Classification with learning k-nearest neighbors[C]∥Proceedings of International Conference on Neural Networks.IEEE, 1996:1480-1483.
[9] LAN X, LI Q, ZHENG Y. Density K-means: A new algorithm for centersinitializationfor K-means[C]∥IEEE International Conference on Software Engineering and Service Science (ICSESS). IEEE, 2015: 958-961.
[10]谢娟英, 高红超, 谢维信. K 近邻优化的密度峰值快速搜索聚类算法[J].中国科学: 信息科学, 2016, 46(2): 258-280.
XIE J Y, GAO H C, XIE W X. Quick search clustering algorithm for kneighbor optimization of density peak [J].Science of China: Information Science,2016,46(2):258-280.
[11]DU M J, DING S F, JIA H J. Study on density peaks clustering based on K-nearest neighbors and principal component analysis[J].Knowledge-Based Systems, 2016, 99: 135-145.
[12]LIU Y H,MA Z M,YU F. Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy[J].Knowledge-Based Systems, 2017, 133: 208-220.
[13]杜沛, 程晓荣. 一种基于 K 近邻的比较密度峰值聚类算法[J].计算机工程与应用, 2019, 55(10): 161-168.
DU P, CHENG X R . A comparison density peak clustering algorithm based on K-nearest neighbors[J].Computer Engineering and Applications,2019,55(10):161-168.
[14]DING S F, DU M J, SUN T F, et al. An entropy-based density peaks clustering algorithm for mixed type data employing fuzzy neighborhood[J].Knowledge-Based Systems, 2017, 133: 294-313.
[15]王飞, 王国胤, 李智星, 等. 一种基于网格的密度峰值聚类算法[J]. 小型微型计算机系统, 2017,38(5): 1034-1038.
WANG F, WANG G Y, LI Z X, et al. A grid-based density peak clustering algorithm[J].Journal of Chinese Computer Systems,2017,38(5):1034-1038.
[16]XU X, DING S F, SHI Z Z. An improved density peaks clustering algorithm with fast finding cluster centers[J].Knowledge-Based Systems, 2018, 158: 65-74.
[17]SRIVASTAV N, HINTON G, KRIZHEVSKY A, et al. Dropout: A simple way to prevent neural networks from overfitting[J].Journal of Machine Learning Research, 2014,15(1):1929-1958.
[18] HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[EB/OL].2012:arXiv:1207.0580[cs.NE].https:∥arxiv.org/abs/1207.0580.
[19]JEBARA T, WANG J, CHANG S F. Graph construction and b-matching for semi-supervised learning[C]∥Proceedings of the 26th Annual International Conference on Machine Learning.New York:ACM,2009:441-448.
[20]LOTFI A, SEYEDI S A, MORADI P. An improved density peaks method for data clustering[C]∥2016 6th International Conference on Computer and Knowledge Engineering (ICCKE). IEEE, 2016: 263-268.
[21]HUBERT L, ARABIE P. Comparing partitions[J].Journal of Classification, 1985, 2(1): 193-218.
[22]PFITZNER D, LEIBBRANDT R, POWERS D. Characterization and evaluation of similarity measures for pairs of clusterings[J].Knowledge and Information Systems, 2009, 19(3): 361-394.
[23]RAND W M. Objective criteria for the evaluation of clustering methods[J].Journal of the American Statistical Association, 1971, 66(336): 846-850.
(編 辑 李 静)
