减法全邻联系数及其在区域水资源承载力趋势分析中的应用

金菊良　何飘　张浩宇　郦建强　陈梦璐　何君

摘要：為进一步挖掘联系数所隐含的各类信息价值以更准确地分析区域水资源承载力发展趋势，利用同一度a与差异度b、对立度c与差异度b之间增量的变化信息，同时将（a-b）当作（b-c）的正向驱动系数、将（c-b）当作（b-a）的负向驱动系数，在此基础上将所得减法邻正联系数加上减法邻负联系数构建减法全邻联系数。将该方法与现有的两种邻联系数方法用于不同地区公共场所卫生监督质量、某医院多年间医疗质量的发展趋势分析比较，同时在区域水资源承载力评价中进行实证应用。结果表明：减法全邻联系数在差异度接近于零的情况也适用，所得结果较其他两种邻联系数方法更接近实际，有助于邻联系数方法的推广应用，对联系数伴随函数的深入研究具有重要意义。用减法全邻联系数计算安徽省水资源承载力3个代表性指标的减法全邻联系数增量曲线与级别特征值增量曲线基本呈对称状态，减法全邻联系数增量的正负可直接用于判断水资源承载力评价指标的发展趋势，为集对事件的发展趋势分析提供了新途径。

关键词：减法邻正联系数;减法邻负联系数;减法全邻联系数;水资源承载力评价;趋势分析

中图分类号：TV87

DOI：10.16152/j.cnki.xdxbzr.2020－03－014

Subtractive full neighbor connection number and its application in

trend analysis of regional water resources carrying capacity

JIN Juliang1， 2， HE Piao1， 2， ZHANG Haoyu1， 2， LI Jianqiang3，CHEN Menglu1，2， HE Jun3

Abstract： In order to further excavate the various information values implied in the connection number， the development trend of regional water resources carrying capacity can be more accurately analyzed. This article regard （a-b） as the forward driving coefficient of （b-c）， （c-b） as the negative driving coefficient of （b-a）， based on the information between the identical degree a and the discrepancy degree b the contrary degree c and the discrepancy degree b. By defining the concept of subtractive positive connection number and subtractive neighbor negative connection number， the expression of subtractive full neighbor connection number is obtained. The subtractive full neighbor connection number and the existing two neighbor connection number methods are compared and analyzed in the trend analysis of health supervision quality in public places and medical quality in a hospital in different years. The results show that the subtraction improves the special case in which the discrepancy degree is close to 0， which is helpful to the perfection of neighbor connection number method and its popularization and application. At the same time， the subtractive full neighbor connection number is applied to the evaluation of water resources carrying capacity in Anhui Province. The results show that the increment curve of three representative indexes and the increment curve of the rank eigenvalue are basically in the state of axial symmetry of the transverse coordinate. The values and increments between the subtractive full neighbor connection number and the level eigenvalue of all indicators are closely negative correlated. Therefore， it can be seen that the positive or negative increment of the subtractive full neighbor connection number can directly judge the development trend of the evaluation index of regional water resources carrying capacity. It provides a new approach for the analysis of the trend of development of set pair events.

Key words： subtraction neighbor positive connection number; subtraction neighbor negative connection number; subtractive full neighbor connection number; water resources carrying capacity evaluation; trend analysis

集对分析（set pair analysis，SPA）是赵克勤［1-2］于1989年提出的一种系统不确定性分析理论。目前针对联系数的结构函数特征已发展出几种联系数的伴随函数，包括减法集对势［3］、偏联系数［4］、效应全偏联系数［5］和邻联系数［6］等，在资源、环境、医疗等领域具有广泛的应用前景。金菊良等［3］提出了减法集对势这一联系数新的伴随函数、并用于判别区域水资源承载力系统在当前宏观期望层次上所处的确定性状态和发展趋势、识别水资源承载力的脆弱性指标。陆广地等［4］将联系数用于学生满意度的综合表述中，运用偏联系数方法对学生满意度作潜在发展趋势的聚类分析。金菊良等［5］为定量描述偏联系数的数学表达形式、揭示偏联系数的物理内涵，采用偏正联系数与偏负联系数相互综合比较分析的方法，提出了基于同异反作用功能的效应全偏联系数，用于评价集对事件的发展趋势。哈丽阳等［6］用邻联系数的势函数分析判断各年度集对事件的发展趋势。孙爱峰等［7］用全邻联系数的数值大小说明不同地区卫生监督质量的发展趋势，为卫生监督管理的科学实施提供重要参考。目前邻联系数计算的方法主要由文献［6-7］提出，这两种方法尚需进一步刻画邻联系数的物理内涵：当差异度b等于零时，无法计算集对事件的全邻联系数及其势函数，只能通过查找对应的趋势表进行判断，且得出的结果无法与同组结果一同排序;全邻联系数的结果通过与数字1的比较判断发展趋势，结果不甚准确，在综合趋势分析中对于单指标多年变化趋势，无法诊断出此指标对于集对事件最终评价结果的影响。为此，本文通过计算同一度a与差异度b、对立度c与差异度b之间的增量，同时将相邻联系分量的变化增量（a-b）作为（b-c）的正向驱动系数、相邻联系分量的变化减量（c-b）作为（b-a）的负向驱动系数，并将减法邻正联系数加上减法邻负联系数来构建减法全邻联系数;将减法全邻联系数与现有的两种邻联系数方法在不同地区公共场所卫生监督质量和某医院医疗质量中进行趋势的比较分析，得出3组不同的计算结果与排序，结合实际情况比较分析这3种方法的适用性;然后将减法全邻联系数应用于安徽省水资源承载力趋势分析中，以进一步验证此方法的适用性。

1 减法全邻联系数的计算

在三元联系数μ=a+bi+cj中a，b，c分别是联系数的同一度、差异度、对立度联系分量［1］。如图1所示，三元联系数当前状态具有正向发展趋势时，通过计算相邻联系分量之间正向的差值判断集对事件往正向发展趋势的大小，即将同一度a与差异度b之间的增量（a-b）作为新的同一度、差异度b与对立度c之间的增量（b-c）作为新的差异度，（a-b），（b-c）表示相邻联系分量之间的差值，自身代表着正方向。联系数的减法邻正联系数可定義为［1， 6-7］：

μ1+=（a-b）+（b-c）i1+  （1）

式中，取i1+=（a-b）［1， 3］，将（a-b）作为（b-c）的正向驱动系数。

由对立统一的观点知事物的发展具有辩证性，对比减法邻正联系数的构造可定义减法邻负联系数。三元联系数当前状态有负向发展趋势时，通过计算相邻联系分量之间负向的差值判断集对事件往负向发展趋势的大小，即将三元联系数中差异度b与同一度a之间增量（b-a）作为新的差异度、三元联系数中对立度c与差异度b之间增量（c-b）作为新的对立度，（b-a），（c-b）表示联系数之间的差值，自身代表着负方向。联系数的减法邻负联系数可定义为

式中，邻正联系数μ+3=a／b+（b／c）i3+，邻负联系数μ-3=（b／a）i-3+（c／b）j，i3+与i3-采用比例取值法求解，j=-1［1-2］。当μ3>1时，集对事件发展趋势是正向;当μ3<1时，集对事件发展趋势是负向;当μ3=1时，集对事件发展趋势为临界状态［7］。

2 实例分析

2.1 邻联系数在某院医疗质量发展趋势分析中的应用

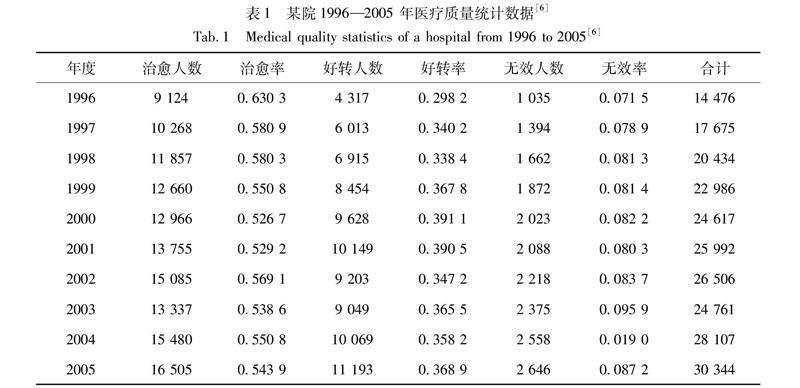
将某院某年度的治愈率、好转率、无效率分别作为联系数中的同一度a、差异度b、对立度c，根据某院1996—2005年的医疗质量统计数据，得到各年度医疗质量的联系数，结果见表1［6］。

由式（1）～（7）计算某院1996—2005年医疗质量的减法邻正联系数、减法邻负联系数、减法全邻联系数μ1，Shi（μ2′）［6］及其排序、全邻联系数μ3［7］的有效值，结果见表2。

由表2可知：①减法全邻联系数增量Δμ1在1997—2000年小于零，表明这4年间医疗质量的发展出现下滑趋势;2001—2002年Δμ1大于零，医疗质量的发展出现上升趋势;2003—2005年间的Δμ1值在正负值间波动，医疗质量状况也处于波动状态。②Shi（μ2′）的排序结果表明，1997—2001年间排序逐渐增加，医疗质量呈下滑趋势;2002年时，医疗质量呈上升趋势;2003—2005年间，医疗质量状况处于波动状态。③全邻联系数μ3的值恒大于1，表明1996—2005年间医疗质量始终处于上升趋势，显示医疗质量的发展趋势恒为正向，这与实际情况不符。④上述3种方法判断1996—2005年间医疗质量的发展趋势中，减法全邻联系数的结果与Shi（μ2′）的结果基本一致，而全邻联系数μ3的计算结果与其他两种方法有较大差异。

2.2 邻联系数在不同地区公共场所卫生监督质量趋势分析中的应用

采用文献［8-9］根据10个不同地区7项卫生监督质量评价指标计算得三元联系数，结果见表3［8-9］。

由式（1）～（7）计算不同地区减法邻正联系数、减法邻负联系数、减法全邻联系数及其排序、Shi（μ2′）［6］及其排序、全邻联系数μ3［7］的有效值及其排序，结果见表4。

由表3、表4可知：①当三元联系数的差异度b=0时，无法计算Shi（μ2′）和全邻联系数μ3，只能对照态势分析表，间接判断所处的趋势，但不能计算出具体的数值，且无法参与排序。②地区A的减法全邻联系数排序第1，地区F的减法全邻联系数排序第10，这是由于地区A的同一度值最大、地区F的同一度值最小，同一度数值的大小是决定地区减法全邻联系数排序结果的主要参考依据。③地区E的同一度值明显小于地区G的同一度值，但是Shi（μ2′）的排序结果是地区E高于地区G，这样的排序结果与实际情况明显不符。将减法全邻联系数排序中地区A，B剔除之后与全邻联系数μ3的排序进行比较，得到的排序结果基本一致，最多相差两个位次（地区E、G、J）。

2.3 減法全邻联系数在安徽省水资源承载力趋势分析中的应用

从《安徽省水资源公报》《安徽省统计年鉴》等［10］中统计筛选2005—2015年各类评价指标的数据和相关资料，采用文献［11-12］给出的安徽省水资源承载力评价指标、等级标准，见表5。

采用文献［3，11-13］的方法计算2005—2015年间安徽省水资源承载力单指标联系数，由式（4）计算3种代表性指标——人均水资源量x1、万元GDP用水量x6和人均GDP x12的减法全邻联系数值及其增量值Δμ1、级别特征值［14］及其增量值，结果见表6。

将表6中各指标的减法全邻联系数与级别特征值［14］、Δμ1与级别特征值增量的关系用折线图展示，如图2至图4所示。

由表6、图2至图4可知：①随着减法全邻联系数的变大，级别特征值逐渐减小、承载状况逐步改善;随着减法全邻联系数的变小，级别特征值则会逐渐增大、承载状况逐步恶化。当减法全邻联系数Δμ1为正值时，级别特征值增量为负值;当Δμ1为负值时，级别特征值增量为正值;当Δμ1趋近于零时，级别特征值增量也趋近于零。②减法全邻联系数增量Δμ1的正负值可用于直接判断此指标的发展趋势，如人均水资源的Δμ1值一直在横坐标上下波动状态，级别特征值增量也不断地处在波动状态，表明指标的发展趋势一直在变化之中，是一个波动性指标，这主要是因为各年的水资源量具有随机性;万元GDP用水量、人均GDP的Δμ1值基本都大于零，级别特征值增量曲线呈下降趋势，表明指标的发展趋势一直为正向，有利于区域水资源承载状况的改善。③减法全邻联系数与级别特征值、Δμ1曲线与级别特征值增量曲线之间具有密切的关联性，它们之间基本呈关于水平线对称的状态，呈现出显著的负相关关系。

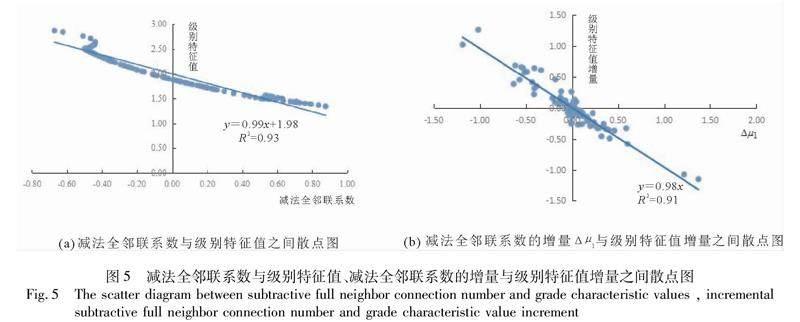
为进一步分析减法全邻联系数与级别特征值、减法全邻联系数增量Δμ1与级别特征值增量之间的相关关系，将安徽省2005—2015年间每年15个评价指标的减法全邻联系数与级别特征值、Δμ1与级别特征值增量全部汇总在一起、画出相应的散点图，如图5所示：

由图5可知：①通过线性拟合分析，减法全邻联系数与级别特征值之间的确定性系数为0.93，有较高的负相关性，减法全邻联系数可判断水资源承载力的变化趋势，但是只有比较减法全邻联系数相邻两个数值的大小，才可以判断出发展趋势。②类似地，减法全邻联系数的增量Δμ1与级别特征值增量之间的确定性系数为0.91，同样呈现出较高的负相关性，因此利用减法全邻联系数的增量Δμ1也可直接判断水资源承载力的变化趋势。③减法全邻联系数与减法全邻联系数增量Δμ1表达的含义基本一致，但是Δμ1的结果更加直观清晰，通过正负值就可判断集对事件的发展趋势。

3 结 论

1）本文通过对减法邻正联系数、减法邻负联系数的概念界定，将邻负联系数转化到正方向上、再与邻正联系数相加，提出了减法全邻联系数μ1的表达式（4），据此可进一步深入挖掘同一度、差异度与对立度之间的关系，得出的结果可揭示出集对事件的总体发展趋势。

2）通过不同地区公共场所卫生监督质量评价和某医院医疗质量趋势判断，用减法全邻联系数与现有的两种邻联系数方法进行了比较分析，再通过安徽省水资源承载力评价的应用研究，进一步分析验证了减法全邻联系数对于集对事件趋势的分析作用，说明了减法全邻联系数的合理性。三个实例的分析和应用结果表明：①运用减法全邻联系数可适用于差异度b等于零时的情况，得到的结果较现有其他两种邻联系数方法更符合实际，同时也符合同一度、差异度和对立度具体数值所代表的含义，所有可能出现的联系数情况都可计算相应的全邻联系数，拓广了全邻联系数的适用范围。②用减法全邻联系数计算的安徽省水资源承载力评价3个代表性指标的减法全邻联系数数增量Δμ1曲线与级别特征值增量曲线基本呈关于水平线对称的状态，受年来水随机不确定性影响的人均水资源量指标的发展趋势一直处在变化之中，是一个波动性指标、具有不确定性，万元GDP用水量、人均GDP指标的发展趋势一直为正向，是稳定改善性指标。③2005—2015年所有指标的减法全邻联系数数值与级别特征值之间有密切的关联，呈现出很强的负相关性，减法全邻联系数增量Δμ1与级别特征值增量之间也存在较强的负相关性。经过实例分析与应用，综合表明减法全邻联系数对于联系数的概念内涵表征是准确、合理的，用减法全邻联系数增量Δμ1可直观准确判断集对事件发展趋势，计算结果符合实际情况。

参考文献：

［1］赵克勤. 集对分析及其初步应用［M］. 杭州： 浙江科技出版社， 2000.

［2］赵克勤， 宣爱理. 集对论——一种新的不确定性理论方法与应用［J］. 系统工程， 1996，14（1）：18－23.

ZHAO K Q， XUAN A L. Set Pair theory： A new uncertainty theory method and application of［J］.Systems Engineering， 1996， 14（1）： 18－23.

［3］金菊良， 沈时兴， 郦建强， 等. 基于联系数的区域水资源承载力评价与诊断分析方法［J］. 华北水利水电大学学报（自然科学版）， 2018， 39（1）： 1－9.

JIN J L，SHEN S X，LI J Q，et al.Assessment and diagnosis analysis method for regional water resources carrying capacity based on connection number［J］.Journal of North China University of Water Resources and Electric Power （Natural Science Edition），2018，39（1）：1－9.

［4］陆广地， 吴宝明， 赵克勤. 用偏联系数与态势函数对高校评价的聚类分析［J］. 数学的实践与认识， 2015，45（19）：50－59.

LU G D， WU B M， ZHAO K Q. With partial connection number and function of university evaluation of clustering analysis［J］.Mathematics in Practice and Theory， 2015， 45（19）： 50－59.

［5］金菊良， 张浩宇， 宁少尉， 等. 效应全偏联系数及其在区域水资源承载力评价中的应用［J］. 华北水利水电大学学报（自然科学版）， 2019， 40（1）： 1－10.

JIN J L， ZHANG H Y， NING S W， et al. Effect full partial connection number and its application in evaluation of regional water resources carrying capacity［J］.Journal of North China University of Water Resources and Electric Power（Natural Science Edition）， 2019， 40（1）：1－10.

［6］哈丽阳， 杨晓燕， 卜让吉. 基于联系数伴随函数的医疗质量发展趋势分析［J］. 中国卫生统计， 2011， 28（1）：68－69，71.

HA L Y， YANG X Y， PU R J. Analysis of development trend of medical quality based on adjoint function of contact number［J］.Chinese Journal of Health Statistics，2011， 28（1）：68－69，71.

［7］孙爱峰， 孙齐蕊. 基于联系数伴随函数的公共场所卫生质量态势和趋势分析［J］. 中国卫生产业， 2015， 12（25）：24－26.

SUN A F， SUN Q R. The situation and trend analysis of public health quality in different areas based on the connection number and associate function［J］.China Health Industry， 2015， 12（25）： 24－26.

［8］任力锋，王一任，张彦琼，等.TOPSIS 法的改进与比较研究［J］.中国卫生统计，2008，25（1）：64－66.

REN L F， WANG Y R， ZHANG Y Q， et al. Improvement and comparison of TOPSIS［J］.Chinese Journal of Health Statistics， 2008， 25（1）： 64－ 66.

［9］汪丽伟， 孙齐蕊， 孙爱峰. 联系数在公共场所卫生监督质量综合评价中的应用［J］. 中国卫生产业， 2014， 11（21）：62－63.

WANG L W， SUN Q R， SUN A F. Application of contact number in comprehensive evaluation of health supervision quality in public places［J］.China Health Industry，2014， 11（21）：62－63.

［10］安徽省统计局， 国家统计局安徽调查总队. 安徽统计年鉴（2001版—2015版）［M］. 北京：中国统计出版社.

［11］李辉， 金菊良， 吴成国， 等.基于联系数的安徽省水资源承载力动态诊断评价研究［J］.南水北调与水利科技， 2018， 16（1）：42－49.

LI H， JIN J L， WU C G， et al. Dynamic evaluation and diagnostic analysis for water resources carrying capacity in Anhui province based on connection number［J］.South to North Water Diversion and Water Conservancy Technology， 2018， 16 （1）：42－49.

［12］CUI Y， FENG P， JIN J L， et al. Water resources carrying capacity evaluation and diagnosis based on set pair analysis and improved the entropy weight method. Entropy， 2018， 20（5）， 359.

［13］WANG W S， JIN J L， DING J， et al. A new approach to water resources system assessment—set pair analysis method［J］. Science in China， 2009， 52（10）：3017－3023.

［14］ZOU Q， ZHOU J， ZHOU C， et al. Comprehensive flood risk assessment based on set pair analysis－variable fuzzy sets model and fuzzy AHP［J］. Stochastic Environmental Research ＆ Risk Assessment， 2013， 27（2）：525－546.

（編 辑 亢小玉）

收稿日期：2020－01－14

基金项目：国家重点研发计划项目（2018YEC0407206）;国家自然科学基金项目（51579059， 51479045）

作者简介：金菊良，男，江苏吴江人，博士，教授，从事水资源系统工程研究。

通信作者：陈梦璐，女，安徽安庆人，博士生，从事水资源系统工程研究。