AANA序列加权和的完全收敛性及完全矩收敛性
2020-04-29何其慧
何其慧
完全收敛性是概率极限理论中非常重要的一个研究内容,它不但可以通过B-C引理建立随机变量的强大数律,也可以得到随机变量加权和的收敛性质及收敛速度.完全收敛性的概念由文献[1]提出.文献[2]引入了关于完全矩收敛性的概念.而且完全矩收敛是比完全收敛更强的一种收敛性质.
在古典概率论中,专家学者们大多假设随机变量之间具有相互独立的关系.在独立关系下,关于随机变量的完全收敛性和完全矩收敛性的研究已日趋完善.然而随着经济社会的发展和研究的进一步深入,学者们发现这种假设在实际应用中是不合理的,大多数据之间都存在一定的相依关系.因此,专家学者们相继提出各种相依随机变量的概念,其中比较著名的是由文献[3]提出的负相协(NA)随机变量.在此假设条件下,文献[4]建立了关于NA 随机变量加权和的完全收敛性的结果.
由上述结果可以得到随机变量加权和的强大数律,因此,很多文献都对其进行了推广.如文献[5-7]分别将定理中α>γ,α=γ及α<γ的情形推广到ρ*-混合随机变量序列;文献[8]将定理推广到NSD 序列下的情形.文献[9]提出了渐近几乎负相协(AANA)随机变量的概念.称随机变量序列{ }Xn,n≥1 为AANA的,同时文献[9]也给出了满足AANA但不是NA的例子.
在适当的条件下,本文将该定理的结果推广到AANA 序列,得到更强的完全矩收敛性的结果,同时得到了关于AANA序列加权和的强大数律.在本文中,C代表正常数,在不同的地方可以取不同值,logx=lnmax(x,e),其中,I(A)表示事件A的示性函数,a+=aI(a≥0) 且a+=-aI(a<0).
1 预备知识

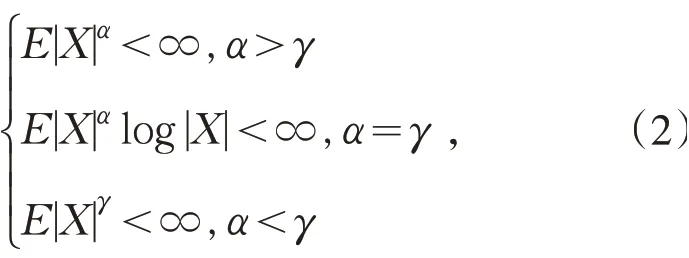
则对任意的ε>0,都有

引理1[7]令{ani,1 ≤i≤n,n≥1} 为满足(1)式的常数阵列,X为随机变量.令其中常数γ>0.则

引理2[7]令为满足(1)式的常数阵列,X为随机变量.令其中常数γ>0.若q>max(α,γ),则
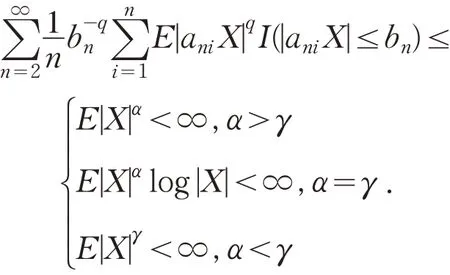
引理3[10]令为AANA 随机变量序列,其混合系数为假设f1,f2,…都为单调非降(或非增)的连续函数,则仍然为AANA 随机变量序列,且其混合系数为{u(n),n≥1} .
引理4[10]令{Xn,n≥1} 为均值为0的AANA随机变量序列,其混合系数满足存在q∈(3 ⋅2k-1,4 ⋅2k-1),使得,其中k为正整数.则存在仅依赖于q的正常数使得对所有的n≥1,
2 主要结果
定理2 令{X,Xn,n≥1} 为同分布的AANA序列,其混合系数满足存在常数q∈(max{3 ⋅2k-1,2γ/α},4 ⋅2k-1),使得,其中k为正整数.{ani,1 ≤i≤n,n≥1} 为满足(1)式的常数阵列,其 中0 <α≤2.记,其中γ>0.当1 <α≤2 时,假设EX=0.如果(2)式成立,则对任意的ε>0,(3)式成立.

由引理3 可知,{Yni,1 ≤i≤n,n≥1} 是混合系数仍然为{u(n),n≥1} 的AANA 随机变量阵列.容易验证
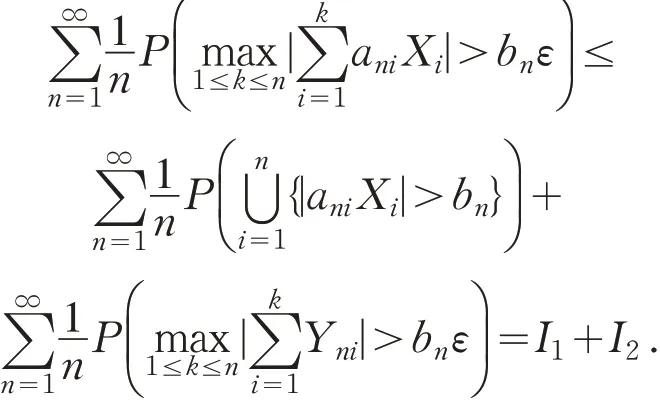
利用概率的次可加性,由Markov 不等式及引理1,得到
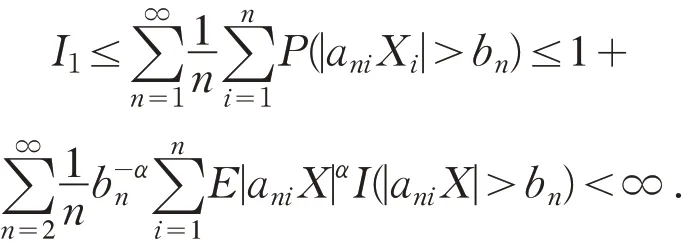
故下面只需证明I2<∞.首先验证

如果0 <α≤1,则由Markov 不等式,(1)式及(2)式,可得

如果1 <α≤2 ,则由EXi=0 ,(1)式及(2)式,可得

因 此(4)式 成 立,从 而 当n充 分 大 时
选取q∈(max{3 ⋅2k-1,2γ/α},4 ⋅2k-1),其中k为正整数.由Markov 不等式,引理4,Cr 不等式及Jensen不等式,可得

注意到q>max(α,γ),由Markov 不等式,引理1及引理2,可得
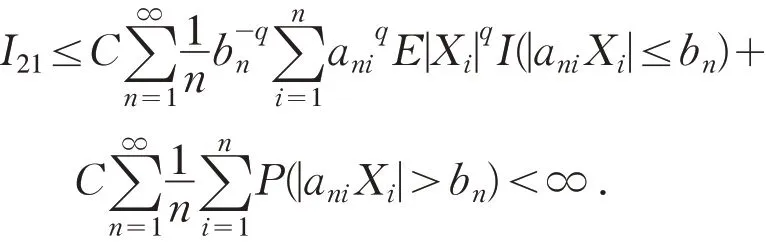
最后将证明I22<∞.由(1)式,Markov 不等式,α≤2 及q>2γ/α可得

注1:注意到若u(n)=0,条件显然成立,此时定理2依然包含定理1的结果.在α>γ和α=γ的情形下,关于混合系数的条件也只需满足存在q∈(3,4) ,使得成立.
定理3 令{X,Xn,n≥1} 为同分布的AANA序列,其混合系数满足存在常数q∈(max{3 ⋅2k-1,2γ/α},4 ⋅2k-1),使得,其中k为正整数,{ani,1 ≤i≤n,n≥1} 为满足(1)式的常数阵列.记,其中γ>0.当1 <α≤2时,假设EX=0.如果(2)式成立,则对任意的ε>0,

证明 不失一般性,假设ani≥0.注意到
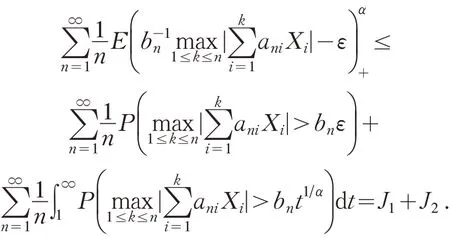
由定理2 可知J1<∞.因此要证明(5)式,只需要证明J2<∞.对任意t≥1,记
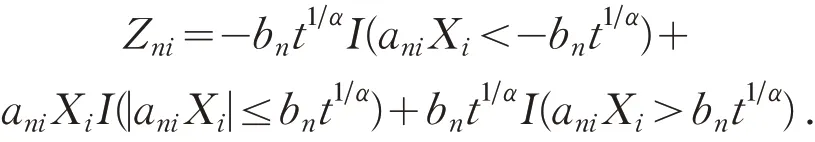
由引理3 可知,{Zni,1 ≤i≤n,n≥1} 是混合系数仍然为{u(n),n≥1} 的AANA 随机变量阵列.注意到

故

由概率的次可加性,引理1及(2)式,可得
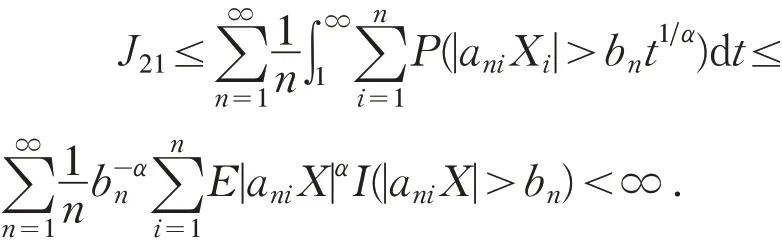
对于J22,首先证明

如果0 <α≤1,则由Markov 不等式,(1)式及(2)式,可得
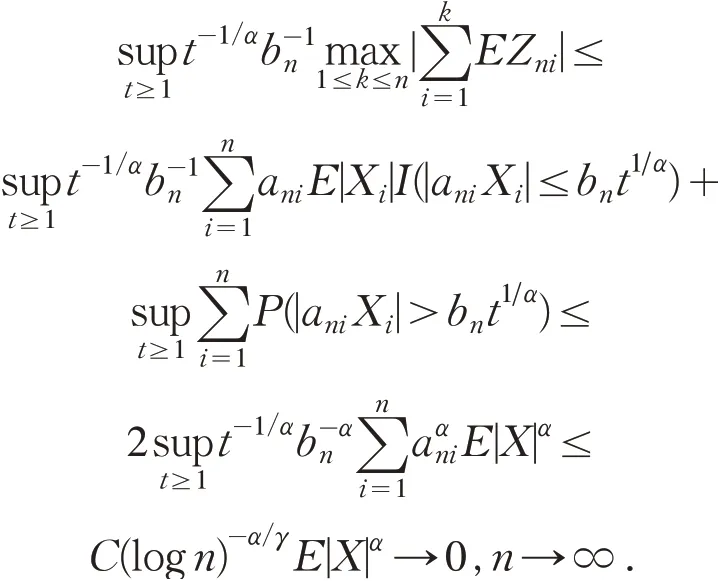
如果1 <α≤2 ,则由EXi=0 ,(1)式及(2)式,可得
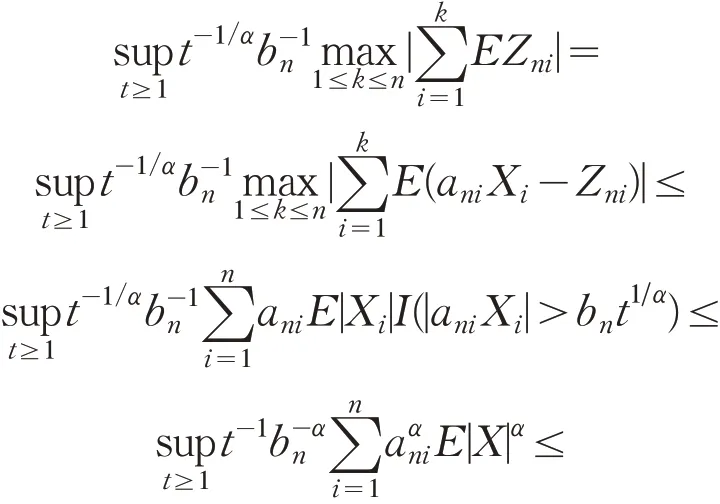

因此当n充分大时,对任意的t≥1 ,都有

取q∈(max{3 ⋅2k-1,2γ/α},4 ⋅2k-1) ,其 中k为正整数,类似I2的处理可得
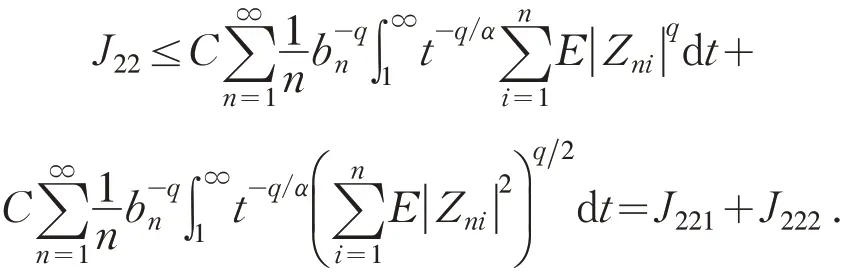
注意到
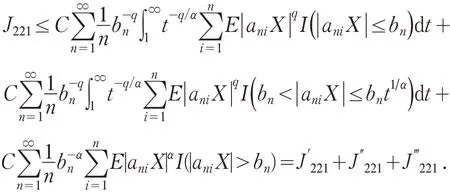
注意到q>max(α,γ),由引理2,得

由引理1得J‴221<∞,以及

最后证明J222<∞.注意到αq/2γ>1,由Cr不等式,Markov不等式及(1)式可得
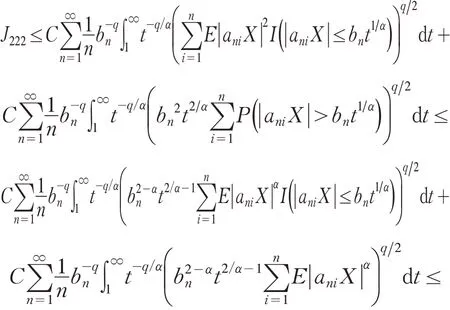

注2:注意到
定理4 令{X,Xn,n≥1} 为一同分布的AANA序列,其混合系数满足存在常数q∈(max{3 ⋅2k-1,2γ/α},4 ⋅2k-1),使得,其中k为正整数.为满足的常数序列,0 <α≤2.记,其中γ>0.当1 <α≤2 时假设EX=0.如果(2)式成立,则
证明 显然由定理1的结果可得
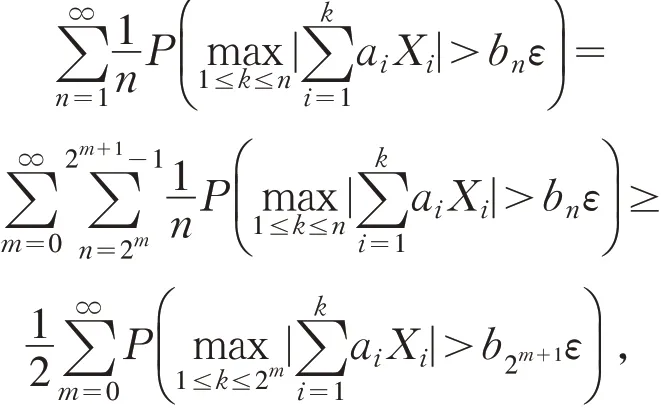
从而由Borel-Cantelli引理,可得

另一方面,对任意的n≥1,总存在m,使得2m≤n<2m+1,因而有

即(6)式成立.
3 结论
本文主要利用AANA 序列的极大值矩不等式,对AANA随机变量加权和的完全收敛性进行了研究,并在相同的条件下进一步建立了完全矩收敛性的结果,改进且推广了文献[4]关于NA序列的结果.作为推论,还得到了AANA 序列加权和形式的强大数律,具有比较重要的理论意义和应用价值.
