高压开关柜尖端放电的电场计算与分析

彭长青， 许超， 尚荣艳， 方瑞明

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021；2. 厦门红相电力设备股份有限公司， 福建 厦门 361000)

高压开关柜广泛应用于电力系统，其运行安全直接影响到供电质量和供电可靠性[1-2].开关柜内部空间紧凑，结构较为复杂，绝缘距离小，容易产生局部放电.据统计，2014年北京市配电网开关柜发生局部放电8次，占开关柜缺陷总数的15%[3].局部放电是影响高压开关柜正常运行的重要因素，将局部放电控制在合理的水平是高压开关柜设计的关键问题.开关柜局部放电的产生与其电场的分布密切相关.近年来，随着电磁场分析软件的发展[4-10]，二维乃至三维空间的电场分析的困难大大降低.周雪会等[11]研究金属尖端电晕放电时，根据试验数据施加仿真模型的激励源.20世纪20年代，Peek[12]在大量电晕实验数据的基础上，总结出计算起晕场强的经验公式，即Peek公式.此后几十年，研究者提出了一些电晕起始判据，如Ortéga公式、Lowke公式、流注起始场强公式、流注起始临界电荷判据，以及气体自持放电的光电离模型等[13].若将这些经验公式与仿真分析结合，研究结果必然更加准确.

湿度也是影响高压开关柜局部放电程度的重要因素[14].中国南方空气湿度高，以福建省厦门市为例，晴天的空气湿度一般都会超过50%，雨天更是达到99%.除此之外，电缆沟道内聚集的污水、高压室的渗水和漏雨等，都可以产生水气进入开关柜内，增加开关柜的空气湿度，甚至在开关柜内部形成凝露.国内外已经展开了湿度对电晕的影响规律研究[15-18]，只是机理比较复杂.很多情况下，并不具备研究局部放电的实验条件，因而有必要建立简便实用的湿度影响放电的经验公式.

为此，本文以高压开关柜的尖端放电为研究对象，提出仿真分析局部放电问题时阈值判据的计算方法，推导出电晕层厚度的计算公式.

1 尖端放电的电场计算

1.1 高压开关柜的尖端放电

高压开关柜容易发生尖端放电有如下6个主要部位[19-24].1) 裸露在空气中的电缆分接头的铜排.因为空气潮湿而产生铜锈，导致铜排表面粗糙不平，形成很多凸起部位.2) 由于制造工艺、生产水平及其他原因，开柜内母线和元器件不能避免地存在棱角、毛刺.3) 某些连接件处的螺丝出牙长度过长.4) 开关柜内掉落的金属异物.5) 因碰撞造成的金属凸起.6) 镀银层剥落的金属尖端.

开关柜内尖端处的电荷聚集，导致电场畸变.相对于其他部位，电场强度更大.当尖端部位的电场强度达到临界场强时，空气将发生局部电离，进而发生尖端放电.

1.2 尖端放电的阈值判据

尖端放电具有极不均匀电场特征，属于“针-板”电晕电场.当“针-板”两电极间的电位差(V)逐渐增大时，最初发生非自持放电；而当V增大到一定数值后，电晕就发生了.该电压就是电晕放电的阈值，称为起晕电压或电晕起始电压或电晕放电阈值电压[25].设针顶端的曲率半径为r，间隙距离为d，电晕层厚度为y，尖端部位电场示意图,如图1所示.

图1 尖端部位电场示意图Fig.1 Schematic of electric field near tip

针电极附近外电场值最大，远离针电极区域空间电场逐渐减小[26].沿着间隙轴心离针顶端x距离处的电场强度[25]为

Ex=2V/{(r+2x)ln[(r+2d)/r]}.

(1)

根据Peek公式，“针-板”正极性电晕起始场强[27-28]为

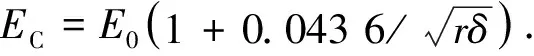
(2)

式(2)中:E0为理想空气的击穿强度，E0=3.0×106V·m-1；δ为相对空气密度，δ=2.92c/α，其中,c为气压(Pa),α为绝对温度(K),文中δ值取1.若在x=0处的场强Ex=EC，则此时两电极间的电位差即为电晕起始电压VC.联立式(1)与式(2)，可得

(3)

1.3 电晕层厚度计算

针顶端区域局部电场很高，发生电离，这个区域称为电晕层，电晕层的边界就是临界电场Ey(理想空气为E0).在这个区域以外，电场弱，不发生或很少发生电离[25].根据式(1)，可以确定电晕层厚度y计算式为

(4)

开关柜的内部结构复杂，在设计开关柜时，计算某些尖端部位的电晕起始电压和电晕层厚度，有助于定性分析发生放电的可能性和放电强度，进而改进开关柜的结构.

1.4 湿度对尖端放电的影响

随着相对湿度H的增加，附着系数η的增加率高于电离系数α，空气间隙中电离减少，电晕起始电压增加.然而，当H超过一定值以后，空气间隙中电离增多，电晕起始电压下降[29].简而言之，电晕起始电压随着湿度的增加呈现先上升后下降，规则比较复杂.就高压开关柜而言，研究湿度高的影响即可.研究表明，湿度小时，电晕起始电压变化量很小，可忽略不计；当湿度足够大(H≥50%)时，电晕起始电压线性下降[30].根据文献[30]的实验数据进行线性拟合，得到电晕起始电压随着湿度的变化关系为

图2 尖端放电有限元分析模型Fig.2 Finite element analysis model of tip discharge

(5)

式(5)中:V′C,V50%分别为考虑湿度和相对湿度为50%时电晕起始电压.

2 尖端放电的电场有限元分析

2.1 有限元分析模型

借鉴《国家电网公司电力设备带电检测仪器年度定期性能检测方案》规定的电晕典型缺陷放电模型，采用Ansoft Maxwell三维电磁场有限元分析软件，搭建尖端放电3D模型，如图2所示.激励源和边界条件:1) 求解域设置为空气；2) 接地电极电位值设置为0 V；3) 尖端为高压电极，设置高电位；4) 尖端曲率半径r=1 mm，针板间隙距离d=4 mm.

2.2 不同湿度下的电晕起始电压

Allen等[31]的研究表明，湿度的增加会使得流注的起始场强E增大，其影响程度ε为

(6)

式(6)中：每当环境绝对湿度ρ改变1 g·m-3，E相应变化ε,ρ0=11 g·m-3.

不同的放电类型，ε的取值也不同，通常不高于5%.取ε=4%进行仿真，得到不同湿度下的电晕起始电压，如表1所示.表1中：Vsi，Vth分别为电晕起始电压的仿真值和理论值.表1中的理论值是根据式(5)计算所得；绝对湿度ρ换算为相对湿度H，取值与实验时相同，以方便后文分析比较.

表1 不同湿度下的电晕起始电压Tab.1 Corona onset voltage at different humidity

2.3 电晕层厚度仿真计算

改变高压电极施加电压，可以得到不同电压(V)时尖端的场强分布情况， 如图3所示. 不同电压下的电晕层厚度(y)，如表2所示.表2中：ysi,yth分别为电晕层厚度的仿真值和理论值；e为误差.

(a) V=5 kV (b) V=10 kV 图3 尖端部位的场强分布Fig.3 Field intensity distribution near tip

表2 不同电压下的电晕层厚度Tab.2 Corona layer thickness at different voltages

从图3和表2可知：电晕层边界的临界电场为理想空气的击穿强度E0.因此，彩虹条下限为3.0×106V·m-1，最外的线条就是电晕层的边界;随着电压的增加，电晕层越厚.

以10 kV为例，不同湿度下的电晕层厚度,如表3所示.表3中：ysi,yth分别为电晕层厚度的仿真值和理论值；er为相对误差.

从表3可知，不改变高电位电压，电晕层厚度随着湿度的增加而增加.另外，表2，3中的相对误差部分偏大，这主要是因为理论计算公式(5)本是经验公式.理论与仿真计算电晕层厚度，尽管相对误差部分偏大，但是绝对误差小，最大不到0.25 mm，足以用来作为确定绝缘距离的参考.

表3 不同湿度下的电晕层厚度Tab.3 Corona layer thickness at different humidity

图4 10 kV高压开关柜局部放电试验平台接线图Fig.4 Partial discharge test platform of 10 kV high-voltage switchgear

3 实验验证

3.1 实验平台

图5 尖端放电模型实物Fig.5 Physical tip discharge model

依据国家行业标准DL/T 417-2006《电力设备局部放电现场测量导则》提供的电力设备局部放电现场设备测量指导，搭建10 kV高压开关柜局部放电试验平台[32]，如图4所示.图4中:交流电源为380 V，三相，50 Hz；调压器的调压范围为0～430 V；试验变压器的额定容量为15 kV·A，额定电压为150 kV/0.38 kV；4) 保护电阻的额定电压为150 kV，额定电流为0.1 A，标称阻值为5 kΩ；电容分压器的额定电压为150 kV，额定电容为300 pF；试验高压开关柜的电压等级为10 kV.

与仿真实验一样，试验开关柜中的尖端放电模型借鉴《国家电网公司电力设备带电检测仪器年度定期性能检测方案》的电晕典型缺陷放电模型，其实物如图5所示.尖端放电区域用有机玻璃密封，针电极采用铜丝进行代替，针尖到板电极之间的距离可调.设置尖端放电模型的间隙为4 mm，针端曲率半径为1 mm；用喷雾器朝模型所在开关柜室喷雾，采用精创GSP温湿度记录仪记录湿度值；采用暂态地电压检测法(TEV)进行局部放电检测.

3.2 湿度对电晕起始电压的影响

改变开关柜室内的湿度，进行局部放电实验，测得不同湿度下的电晕起始电压，如表4所示.

表4 不同湿度下的电晕起始电压Tab.4 Corona onset voltage at different humidity

发生尖端放电时，局部放电检测仪采集的放电点分布，如图6所示(取相对湿度79.8%所得的放电点分布).根据表1的理论值、仿真值和表4的实验值，电晕起始电压随相对湿度的变化，如图7所示.

计算得到电晕起始电压仿真值、实验值和理论值的相对误差，如表5所示.表5中：esi,eexp分别为相对误差的仿真值和实验值.

图6 尖端放电点分布 图7 电晕起始电压随相对湿度变化 Fig.6 Tip discharge point distribution Fig.7 Corona onset voltages at different relative humidity

表5 电晕起始电压的相对误差Tab.5 Relative error of corona onset voltage

从图7与表5可知:不同的相对湿度下，无论是仿真、还是实验，电晕起始电压与理论值相近，式(6)可以反映湿度对开关柜尖端放电的电晕起始电压的影响；湿度对高压开关柜尖端放电的电晕起始电压影响很大，相对湿度越大，电晕起始电压越小.

4 结论

1) 以高压开关柜的尖端放电为研究对象，提出仿真分析局部放电问题时阈值判据的计算方法，并推导出电晕层厚度的计算公式.理论计算与仿真分析结合，研究局部放电必然更加准确.

2) 湿度是影响高压开关柜局部放电的重要因素，然而，湿度对电晕特性的影响规律复杂.通过分析实验数据，可以得到电晕起始电压随着相对湿度的变化公式.这个公式化繁为简，非常实用.

3) 计算电晕层厚度、电晕起始电压，并分析湿度对它们的影响，有助于判断是否有可能发生放电；同时，定性分析放电强度，确定绝缘距离，进而可以改进开关柜结构.这可避免某些地方间隙太小，或者某些地方过尖锐，从而导致放电.

4) 文中的计算分析方法可以供其他需考虑电晕问题的电气设备(如电机、变压器)参考.