微型齿轮的机器视觉检测系统设计

2020-04-29魏东亮周迪斌张家瑜马建峰解利军

计算机测量与控制 2020年4期

魏东亮,周迪斌,张家瑜,马建峰,解利军

(1.杭州师范大学杭州国际服务工程学院，杭州 311121;2.杭州手表有限公司，杭州 310015; 3.浙江大学航空航天学院，杭州 310028)

0 引言

在精密机械行业，微型擒纵轮(见图1)是一种常见的微型齿轮。擒纵轮在生产过程中容易出现断齿的问题，因此，在组装设备之前必须进行质量检测。传统的检测方法主要是人工检测，工人通过显微镜放大零件图像，并对照标准的图纸判断是否有断齿。人工检测依赖个人经验，主观性强，易疲劳，导致产品质量管理的不稳定，且难以量化评估。采用机器视觉技术进行质量检测是行业发展趋势，其能有效保证产品检测的准确度和稳定性。

图1 擒纵轮

数字图像以像素(pixel，px)为基本单位，在边缘检测时，为提高精度，经常需要进行亚像素级别的定位。亚像素边缘是指将边缘附近的像素进行分解，从而精确定位边缘[1]。常用的亚像素检测方法[2-3]有矩法、最小二乘方差法、插值法及拟合法等。

文献[4-5]提出了两种基于Zernike矩的亚像素边缘定位法。文献[6-7]提出了两种基于高斯拟合的亚像素边缘检测算法。文献[2,8-9]提出了基于二次曲线拟合的亚像素定位模型，该模型在理想条件下定位精准度高。文献[10]提出了一种通过三次多项式拟合的亚像素边缘定位方法，该方法能够达到较高的精度。本文参考以上文献，使用一种基于局部区域特征的三次曲线模型来计算亚像素位置，这种模型考虑了局部的特征和边缘梯度，精度高，速度快，能够满足项目的需要。

对于齿轮齿长缺陷的检测，目前常用的方法有灰度值比较法[11]、直线拟合法[12]、图像特征识别的方法[13]等。这些方法一般都要求镜头面向轮片，如果需要同时检测轮片的平整度就会迫使系统变得更加复杂。针对机械行业中微型齿轮需要同时检测齿长误差和轮片平整度等多个指标的情况，本文提出一种中点极差分析的方法，可以在齿轮竖直放立的情况下同时检测齿长误差和轮片平整度等多个指标，检测效率高。

1 系统总体设计

1.1 光学方案设计

根据本项目的特点，要求系统必须满足以下几点：1)所采用的光学系统成像要清晰，对比度好，噪声少；2)算法能够精确地计算出检测目标的边缘线；3)算法必须具有一定的鲁棒性，比如能够自动矫正一定的倾斜角度，能够在亮度不太理想的情况下自动矫正对比度，准确定位目标区域。

微型擒纵轮体积微小，为了减少拍摄产生的边缘虚影，所以选择平行背光源，镜头采用高分辨率低畸变的远心镜头。检测系统采用视频检测方式，零件放置在专用的工作台上，使用导气管送气吹动零件转动。工作台如图2所示。

图2 工作台

1.2 算法框架

齿轮齿长误差检测依次经历如下步骤:图像采集与预处理，倾角矫正，感兴趣区域(region of interest，ROI)垂直边缘的亚像素位置计算，齿轮中心位置计算，中心位置动态极差计算，齿长合格判定。图3显示了这个流程框架。

图3 算法流程

2 边缘检测与亚像素定位

2.1 图像采集和预处理

2.1.1 图像去噪

齿轮表面有时候会附着一些细小的灰尘颗粒，工作的环境也可能存在光线不理想等情况，这样得到的零件图像上常常会存在一些噪声。噪声的存在会干扰目标的识别和边缘的精确定位，所以需要对噪声进行处理。

目前去噪的方法主要有空间域处理法和频率域处理法。空间域处理法常见的有均值滤波、中值滤波、高斯模板卷积等方法，这些方法在滤除噪声的同时往往会破坏图像边缘等细节，使图像变得模糊。本系统需要精确定位微型齿轮的边缘，所以空间域处理法不是首选。频率域去噪方法常见的有基于傅里叶变换的方法、基于离散余弦变换的方法、基于小波变换的方法等。其中小波变换方法在空域和频域都具有良好的局部化特性，在去除噪声的同时能保持图像细节，提高图像的质量。基于以上分析，本系统采用小波变换的方法进行去噪处理。

小波变换去噪方法的原理如下：使用滤波器把含有噪声的图像信号分解到各尺度中，在每一尺度下把属于噪声的小波系数去掉，保留并增强属于信号的小波系数，最后再经过小波逆变换恢复图像信号。小波变换使用的滤波器一般由一个低通滤波器和一个高通滤波器组成。图像信号通过低通滤波器得到其低频分量，通过高通滤波器得到其高频分量，噪声一般属于高频分量，高频分量可以再继续分解下去。小波变换可以选择不同的变换函数，以获得最佳的效果。使用coif2小波基函数进行去噪，效果如图4所示。

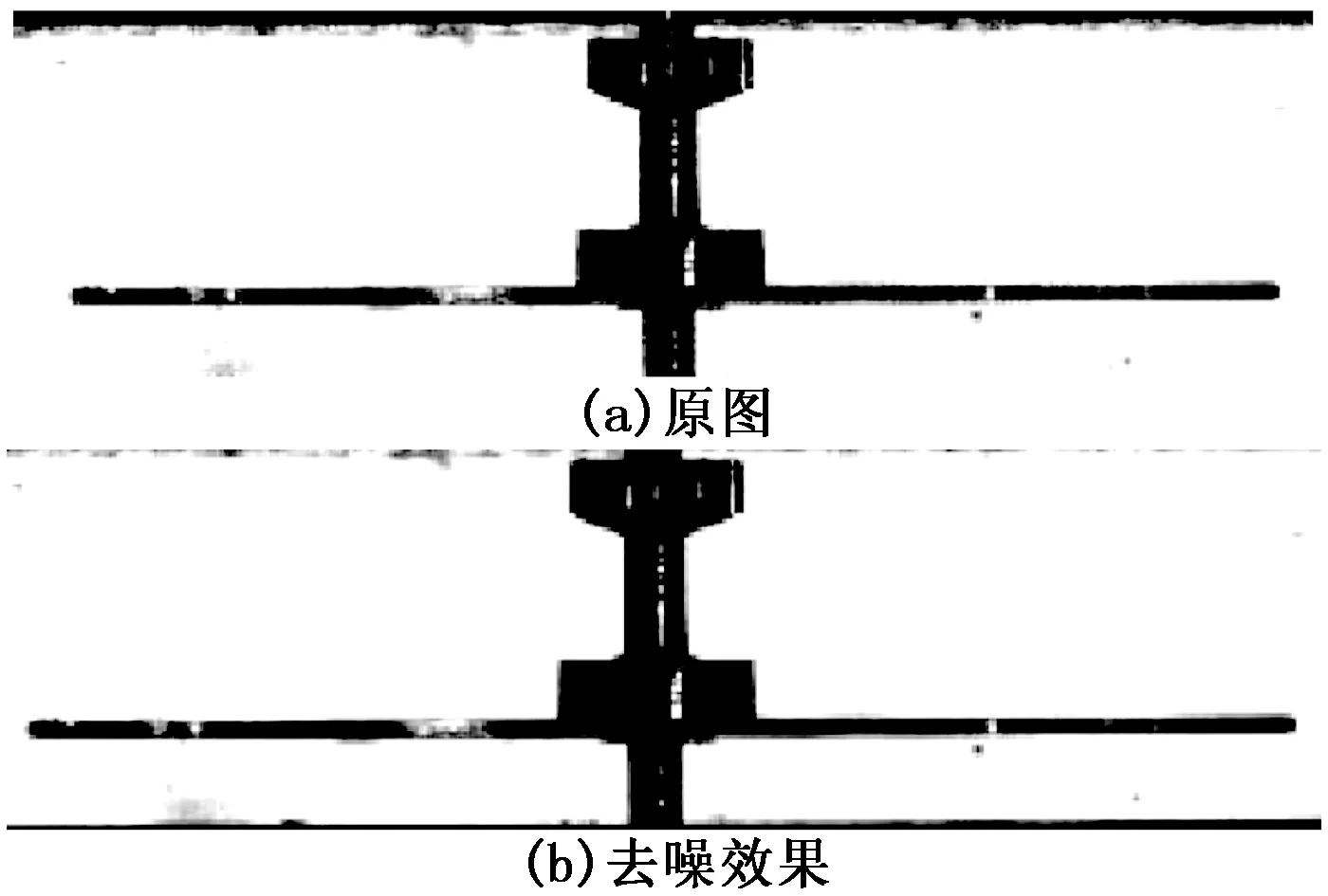
图4 小波去噪

从图4可以看出，小波变换可以满足项目需要的去噪效果。

2.1.2 阈值分割

齿轮图像中背景为白色，目标为黑色，原图中在零件边缘处会有一些虚影，为增强对比度，消除虚影，需要进行阈值分割。实验中分别使用固定阈值法、最大类间方差法、迭代阈值法、P参数法进行二值化处理，结果表明固定阈值法二值化效果最好，最佳阈值的经验值为100。固定阈值法实验结果如图5所示。

图5 二值化

2.2 图像矫正

零件在采样的过程中容易存在一定的倾斜，倾斜的角度一般在水平线上下30°之内。目前常用的倾角矫正方法有：基于投影的方法、基于Hough变换的方法、基于Radon变换的方法、基于线性拟合的方法等。本文采用基于Radon变换的方法。

相比较于Hough变换方法，Radon变换方法的抗干扰性更好，效率更高。Radon变换直线检测算法采用穷举式搜索将待检测图像的灰度分布函数沿不同方向的直线积分路径积分，找出超过给定阈值的积分极大值点，则图像中待检测直线方向就垂直于该极大值点的直线积分路径。在Radon变换检测出的直线中，找到位于零件正常倾斜范围的直线，将其倾斜角度作为零件倾斜的角度，然后进行反向旋转即可矫正图像。

设f(x,y)为一个二维函数，则Radon变换[14-15]定义如下式：

(1)

Radon变换将原图像空间中的直线映射为(ρ,θ)参数空间中的点(线积分值)，原来在图像空间上的一条直线的所有的点在参数空间上都位于同一点。记录参数空间上的点的积累厚度，便可知图像空间上的线的存在性。因而，对原图像中直线的检测可转化为对参数空间中点的检测。

Radon变换矫正图像步骤为：

1)读入原图像并转化为灰度图，使用canny算子进行边缘检测。

2)对图像在-90～90°上进行Radon变换。

3)提取变换后最大峰值点对应的角度α,α=α-91，如果满足-45≤α≤45，则将此α作为图像的水平倾斜角，如果不满足则继续查找剩下的最大峰值对应的角度，直到找到属于[-45,45]的角度并以此作为图像的倾角θ。

4)对图像旋转-φ，完成矫正。

使用以上方法能够矫正擒纵轮图像的倾斜，如图6所示。

图6 图像矫正

2.3 ROI亚像素位置计算

本文采用一种基于局部区域特征的三次曲线模型来计算亚像素位置，该模型针对每个可能的边缘像素，选取一个5×3的模板，并在模板区域内计算一个三次曲线，利用此曲线确定边缘点的亚像素位置。三次模型需要基于一次模型进行推导，故先介绍一次模型。

2.3.1 一次函数模型

如图7所示，假设直线L:y=kx+b是图像中的边缘，且L将图像分成上下两部分，分别记做M和N。这两部分的面积分别记做SM，SN，M，N也表示M，N两部分的平均灰度值。直线L所在的坐标系原点为(i,j)，设(i,j)处像素的灰度值为F(i,j)，它也表示整个模板区域的平均灰度值。设模板区域总面积为S[2]。则有：

S=SM+SN

(2)

(3)

图7 一次函数模型

考虑中间像素(i,j)的5×3邻域模板，以L2、M2和R2来表示模板中直线L下侧左、中、右列的像素面积，如图8所示。直线L坐标系原点的位置依然是O(i,j)，l列中心的横坐标是i-1，r列中心的横坐标是i+1；最上一行的中心位置纵坐标是j+2，最下一行中心位置的纵坐标是j-2；设每个像素格的边长为w。

图8 5×3模板

(4)

(5)

(6)

设5×3模板中左边一列的像素灰度值之和为Tl，中间一列为Tm，右边一列为Tr，则有：

(7)

将式(3)代入，可得：

(8)

(9)

(10)

2.3.2 三次函数模型

一次函数模型是三次函数模型三次项系数和二次项系数都为0时的特殊形式，使用三次函数模型来预测边缘点的亚像素位置会比一次函数模型更精确一些。三次函数模型预测亚像素位置如图9所示。各数学符号还保持前面的定义，假设曲线f：y=ax3+bx2+cx+d为图像中的边缘。

图9 三次函数模型

边缘下侧左、中、右部分面积计算：

(11)

(12)

(13)

式(8)～(10)在3次函数模型中依然成立。将式(11)～(13)代入式(8)～(10)中，可以解得：

(14)

由式(14)可知，三次函数模型下像素点(i,j)对应的亚像素位置为(i,j-d)。

在上面的公式中，M，N代表了边缘两侧平均灰度值，|M-N| 则代表了边缘两侧的梯度幅值，其方向为边缘的梯度方向。

设点O(x,y)处沿x方向的偏导数为fx，沿y方向的偏导数为fy。当fx·fy>0时，设Δx=1；反之，Δx=-1。

(15)

(16)

将式(15)、(16)代入式(14)，即可求得三次函数模型下的亚像素位置。

在使用上述模型之前必须先粗略定位出边缘的位置。对于每个边缘点，使用上述模型求解其亚像素位置。

2.4 计算边缘直线

如图10所示，我们需要描绘出ROI垂直边缘的直线。可以使用投影法来生成直线。投影法是通过计算图像在水平和垂直边缘上的像素点的个数来确定边缘的位置。

图10 ROI垂线边缘线

投影法生成垂直线的方法如下： ROI(图中矩形框中的区域)中以列为单位，统计每列的像素数，相当于往x轴投影，如下面的式(17)所示，其中f(i,j)为(i,j)处的像素值。为了利用计算前面得到的亚像素位置,i,j的增量都设置为0.5 px,即将1个像素点分解为4个亚像素点,这样就可以将边缘精确到0.5像素:

(17)

其中:当f(i,j)>d时，f(i,j)=1，当f(i,j)≤d时，f(i,j)=0，Δy是ROI在y轴方向的长度，阈值d取100。

在图11中，从左往右依次是黑色区域，白色区域，所以生成的Vi数组从左往右依次是谷，峰，取峰值处的横坐标x0为生成的垂直线段L1的起点P1的横坐标，L1的终点P2的横坐标也取x0，P1、P2纵坐标取ROI沿y轴方向的起点和终点的纵坐标，连接P1，P2即得到垂直线段L1。

图11 投影法原理

3 齿长误差测定

3.1 中点极差法原理

实验中擒纵轮外围的齿数为20个，属于偶数。从图12中可以看到，20个齿均匀分布在齿轮外围，每个齿所占有的弧度相等，齿的特征也完全相同，所以整个齿轮呈现中心对称的特征。过圆心的直线与两端齿的交点总是处于齿的同一个特征位置。如图13，为了判断断齿情况，可以利用齿轮直径的两个端点A，B的位置计算出中点O的位置，并通过计算一定数量帧的圆心O位置的极差来确定。这一方法在本文中称为中点极差法。

图12 齿轮对称特性

图13 中点极差法图

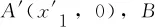
图14 断齿偏移分析图

无断齿时，有：

(18)

设断齿所缺失的部分长度为d，先考虑右侧断齿情况：

d=|x2-x2′|

(19)

(20)

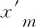
Δxm=|Δxm1|+|Δxm2|=d

(21)

由式(21)可知，中点位置偏移量Δxm可以代表断齿的缺失长度d，所以，可以通过计算一定数量的中点位置极差来判断断齿情况。

3.2 中点偏移量有效范围

中点偏移量只能在一定范围内表示断齿的缺失长度。如图15所示，设OP，OQ是紧邻的两个齿，OP位于水平位置。

图15 中点偏移量有效范围

(22)

PM=OP-OM=OP-OQ·cosθ

(23)

中点偏移量:

Δxm≤|PM|

(24)

所以，使用Δxm代表d仅当d≤|PM|时成立。代入产品的参数，可以求得|PM|=21 cmm(忽米，丝)。

3.3 单位换算关系

工业上描述微观尺寸误差时经常使用的测量单位是忽米，而数字图像的单位是像素。如图16所示，测量得到轮片的厚度为30 px，实际厚度为12 cmm，所以得出换算关系：1 cmm=2.5 px，1 px=0.4 cmm。

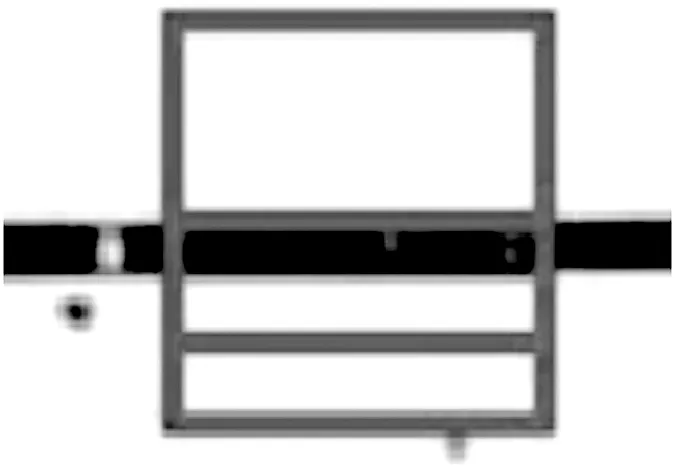
图16 擒纵轮厚度测量

4 实验结果与分析

根据企业的规定，本文所述的这种擒纵轮齿长的合格标准是最大偏差小于等于2 cmm。根据前面的分析，中点极差法中点位移偏差在21 cmm以内都是有效的，所以中点极差法适合测量此种类型的擒纵轮。

为了检测算法的稳定性，对400个零件进行了测试，其中200个合格品，200个断齿缺陷品。对于每一个零件的检测结果，都与人工检测结果进行比对。软件检测结果如表1所示。

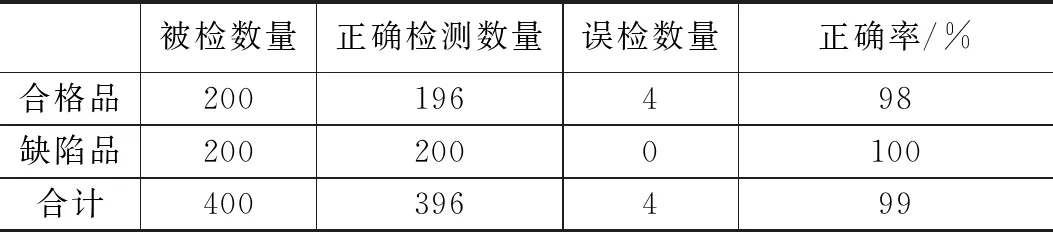
表1 软件检测实验

经分析，出错的原因在于当擒纵轮轮片不平整情况严重时会导致图像左右摆动幅度增大，从而导致误判。轮片平整度偏差大于2 cmm时属于不合格品。实验表明，只有当轮片平整度超出合格范围时其对左右摆动的影响才会比较明显，此时可能导致误判为断齿，而平整度小于2 cmm的合格品一般不会影响断齿的判定。所以，虽然少数非断齿品可能误判为断齿，但并不影响对该零件整体质量是否合格的判定。

通过亚像素算法得到的像素点的位置是浮点型数据，根据下面的式(25)将亚像素位置精确到0.5 px的整数倍。