基于PNN的汽车ABS系统中压力调节器和轮速传感器的故障诊断

孙丽娜，王佳庆，黄永红

(1.苏州工业园职业技术学院 机电工程系，江苏 苏州 215123；2.江苏大学 电气信息工程学院，江苏 镇江 212013)

0 引言

随着汽车科技的进步，汽车的速度在不断地提高，当汽车在高速下制动或在滑溜路面上制动的过程中，由于汽车的车轮产生抱死现象，很可能会出现车尾偏离行驶方向、汽车旋转掉头、驾驶员控制不了汽车行驶方向等危险状况，从而造成交通事故[1]。汽车防抱死制动系统(anti-lock braking system,ABS)是指在汽车被要求强制减速或停车时，为了防止车轮被抱死，其能够自己主动地控制制动器可达到的最大滚动摩擦力的大小，使车轮处于边滚边滑(滑移率在20%左右)的状态，以保证车轮与地面的附着力在最大值的一种主动安全装置[2-4]。

目前针对汽车防抱死制动系统的故障诊断大多采用的是BP神经网络，但是BP神经网络存在收敛速度慢、容易陷入局部极小值的问题，并且在使用BP神经网络进行训练时，即使同一网络模型每次训练的结果也都不相同[5]。概率神经网络(probabilistic neural network,PNN)是基于Bayes分类规则和Parzen窗的概率密度面数估计方法发展而来的并行算法[6-7]。由于PNN结构简单、训练简洁、在故障诊断方面得到了广泛的应用。

在汽车防抱死制动系统中，压力调节器和轮速传感器起着非常重要的作用，为了进一步地完善汽车防抱死系统的制动性能，本文利用概率神经网络对ABS系统的压力调节器和轮速传感器进行故障诊断，并与BP神经网络进行了比较。结果表明概率神经网络诊断耗时短，并且网络一旦确定，训练结果不会改变。

1 防抱死制动系统的结构

典型的气动ABS系统结构如图1所示。

由图1可以看出，防抱死制动系统主要由轮速传感器、压力调节器(ABS调节器)、电子控制单元(ECU)三部分组成，另外还包括制动气室、储气筒、制动踏板、继动阀、三通阀等。压力调节器是汽车防抱死系统中最主要的执行机构，每个控制通道中各设置一个压力调节器，每个调节器分别对相应的车轮进行控制。每个车轮上各安装一个转速传感器，将有关的车轮转速的信号传送到电子控制单元(electronic control unit,ECU)。ECU根据各车轮转速传感器输入的信号对各个车轮的运动状态进行监测和判定，并形成相应的控制指令。压力调节器受ECU的控制，对各制动轮的制动压力进行调节。

如果防抱死制动系统的压力调节器发生了故障，当踏下制动踏板时，气体压力将直接进入制动气室，车轮会突然抱死；如果汽车防抱死系统的轮速传感器发生了故障，那么相应车轮轮速就不能被识别而处于独立运行状态，这时ABS调节阀接收不到速度信号将会非常危险。因此对压力调节器和传感器进行故障诊断非常重要。

2 概率神经网络

概率神经网络[8-9]的结构如图2所示。

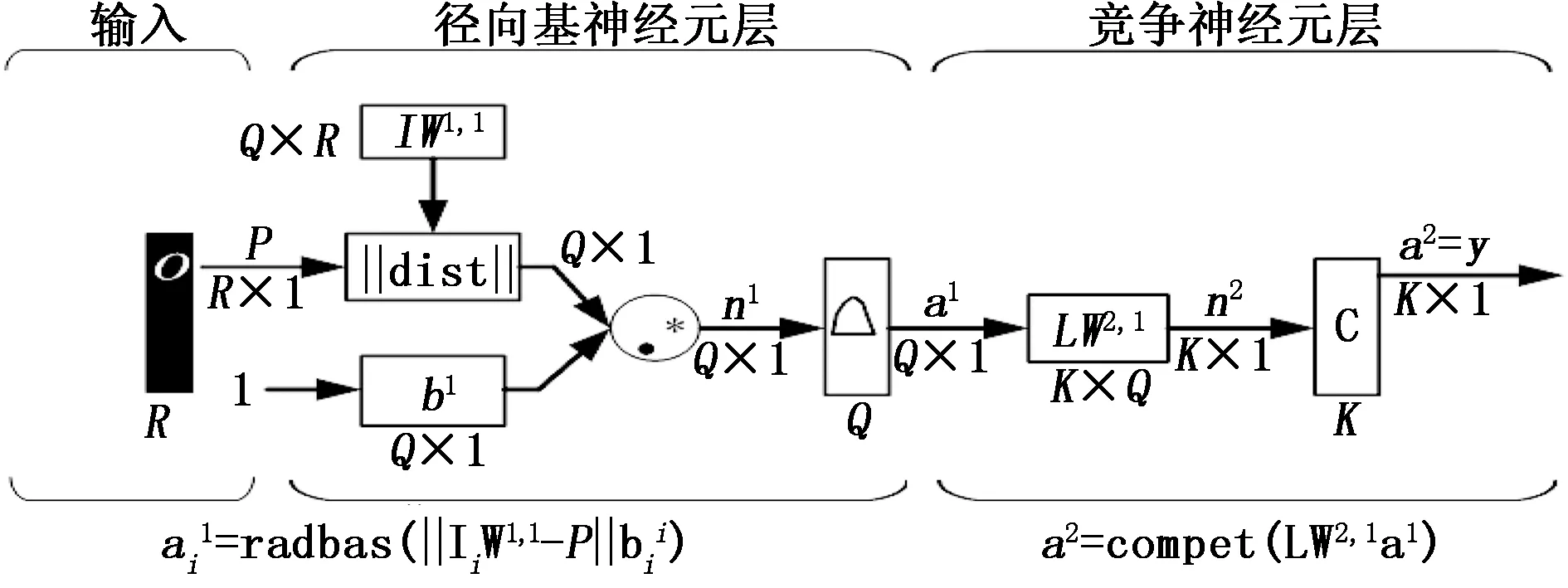
图2 概率神经网络结构

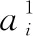
将PNN的第一层径向基神经元的输入权值矩阵IW1,1设为Q个训练样本对的转置P′。当网络获得到输入时，由|dist|函数计算得到一个向量。然后将该向量中的元素与偏差向量b中的元素逐个相乘，并把计算结果传送给 radbas函数。经过radbas函数计算之后，看输入向量与哪一个样本向量最接近，则a1中对应的元素就接近于1。如果输入向量与一系列训练样本向量都接近的话，那么对应的几个元素的值都接近于1。

PNN的第二层权值矩阵LW2,1设为期望目标响应T。权值矩阵的每一个行向量中只有一个元素的值为1，对应着一类输入，其余元素的值均为0，然后计算矩阵乘积Ta1。最后，第二层神经元采用竞争传递函数计算n2，对其中最大的元素输出为1，其余元素取为0。从而，PNN就完成了对输入向量的划分。

3 ABS系统故障诊断模型的建立

3.1 输入输出样本的收集与设计

通过分析ABS系统的工作原理，并结合实际的运行经验，确定网络的输入和输出变量。本文只针对高附着路面，起车时制动及单一的压力调节器或传感器发生故障时进行研究。

3.1.1 确定网络的输入与输出

在ABS系统中，压力调节器会出现无故障F1、左前调节器故障F2、右前调节器故障F3、左后调节器故障F4、右后调节器故障F5共5种故障类型。每种类型所对应的纵向车速P1、侧向车速P2、左前轮轮速P3、右前轮轮速P4、左后轮轮速P5、右后轮轮速P6的变化趋势不同。因此在对压力调节器进行故障诊断时，确定P1、P2、P3、P4、P5、P6作为压力调节器故障诊断模型的输入变量，F1、F2、F3、F4、F5作为压力调节器故障诊断模型的输出。用二进制的形式描述这5种故障类型分别为(1 0 0 0 0)，(0 1 0 0 0)，(0 0 1 0 0)，(0 0 0 1 0)，(0 0 0 0 1)。

在ABS系统中，轮速传感器会出现无故障Y1、左前轮传感器故障Y2、右前轮传感器故障Y3、左后轮传感器故障Y4、右后轮传感器故障Y5共5种故障类型。每种类型所对应的纵向车速X1、侧向车速X2、左前轮轮速X3、右前轮轮速X4、左后轮轮速X5、右后轮轮速X6的变化趋势也不同。所以在对轮速传感器进行故障诊断时，确定X1、X2、X3、X4、X5、X6为轮速传感器故障诊断模型的输入变量，Y1、Y2、Y3、Y4、Y5为轮速传感器故障诊断模型的输出。用二进制的形式描述这5种故障类型分别为(1 0 0 0 0)，(0 1 0 0 0)，(0 0 1 0 0)，(0 0 0 1 0)，(0 0 0 0 1)。

3.1.2 网络输入输出样本的采集

无故障时仿真条件为：路面附着系数为0.4，100%滑转的附着系数为0.3，变速器5档，4个车轮制动力都为4e6N·m，初始车速22.5 m/s。参数KP为290，KI为70。

压力调节器发生故障的仿真条件为：把哪个车轮制动力达到最大12e6N·m(其他仿真条件与无故障时相同)，就认为哪个压力调节器发生故障。在进行数据采集时，每种故障取10个样本(5种故障)，即0.3、0.4、0.5、0.6、1.5、1.8、3.2、3.8、4.2、4.5 s时的速度值，总共采集了50个样本。

轮速传感器发生故障的仿真条件：把哪个轮速信号断开(其他仿真条件与无故障时相同)，就认为哪个轮速传感器发生故障。在进行数据采集时，每种故障取7个样本(5种故障)，即2、2.5、3、3.5、4、4.5、4.7 s时的速度值，总共采集了35个样本。文实验数据来自参考文献[10]。

3.2 故障诊断模型的建立

3.2.1 压力调节器故障诊断模型的建立

针对压力调节器的故障诊断，将0.3、0.4、0.5、0.6、1.8、3.2、3.8、4.2、4.5 s时所采集的数据作为训练样本。为了验证概率神经网络的故障诊断能力，本文将概率神经网络与BP神经网络进行比较。在BP神经网络训练过程中，用newff函数构建一个BP神经网络。其参数设置如下：隐含层采用对数S型传递函数logsig，输出层采用线性传递函数purelin，训练函数采用基于Levenberg-Marquardt的BP算法训练函数trainlm，网络的最大训练次数设置为2000，训练误差设置为0.001。另外，BP神经网络隐含层节点个数的选取非常重要，本文根据公式(1)确定隐含层节点的取值范围。

(1)

式中，m为网络的隐含层节点的个数，n为网络的输入层节点的个数，l为网络的输出层节点的个数，α为1～10之间的常数。从3.1.1节可以看出，在对压力调节器进行故障诊断时，输入节点的个数为6，输出节点的个数为5，代入公式(1)，计算得m的取值为4～14。表1为隐含层节点在4～14范围内时，利用BP神经网络对压力调节器进行故障诊断模型的训练结果。

表1 BP神经网络训练结果(压力调节器故障)

从表1中可以看出，当隐含层节点数为14时，网络训练所得到的的均方根误差最小，其值为0.012 4，此时网络的平均绝对误差为0.033，训练时间为0.826 8 s，迭代次数为12次，此时网络训练过程的误差变化如图3所示。

图3 网络训练过程的误差变化(压力调节器故障)

从图3中可以看出，当训练次数达到12步时，达到了预设的训练误差0.001，网络训练收敛。

在概率神经网络训练过程中，利用newpnn函数建立网络，newpnn的函数形式为:net=newpnn(P，T，spread)。其中P为网络的输入向量，T为网络的输出向量，平滑因子spread的取值对网络的训练性能产生很大的影响。本文在利用概率神经网络对压力调节器的故障诊断模型进行训练时，平滑因子的取值选取从0.1～10(间隔为0.1)，训练结果如表2所示。

表2 PNN平滑因子取值

从表2中可以看出，当平滑因子取值为0～1.6时，网络训练的平均绝对误差为0。当平滑因子取值为1.7～10的过程中，随着平滑因子取值的增大，平均绝对误差也会阶段性的增加。当平滑因子取值为0～1.6时，所对应的网络训练时间如表3所示。

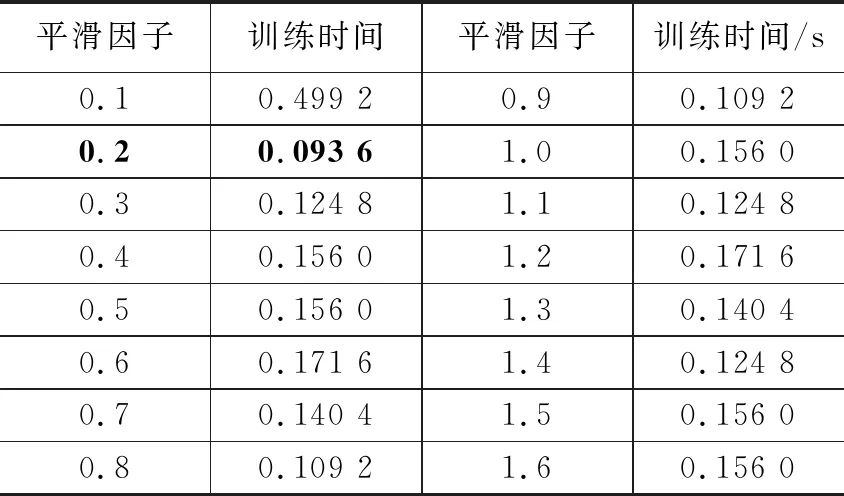
表3 PNN训练时间

从表3中可以看出，当平滑因子的取值为0.2时，训练时间最短为0.093 6，所以平滑因子的取值选为0.2。和BP神经网络相比，BP神经网络的训练时间是PNN的8.8倍，PNN训练后训练数据的分类效果如图4所示。

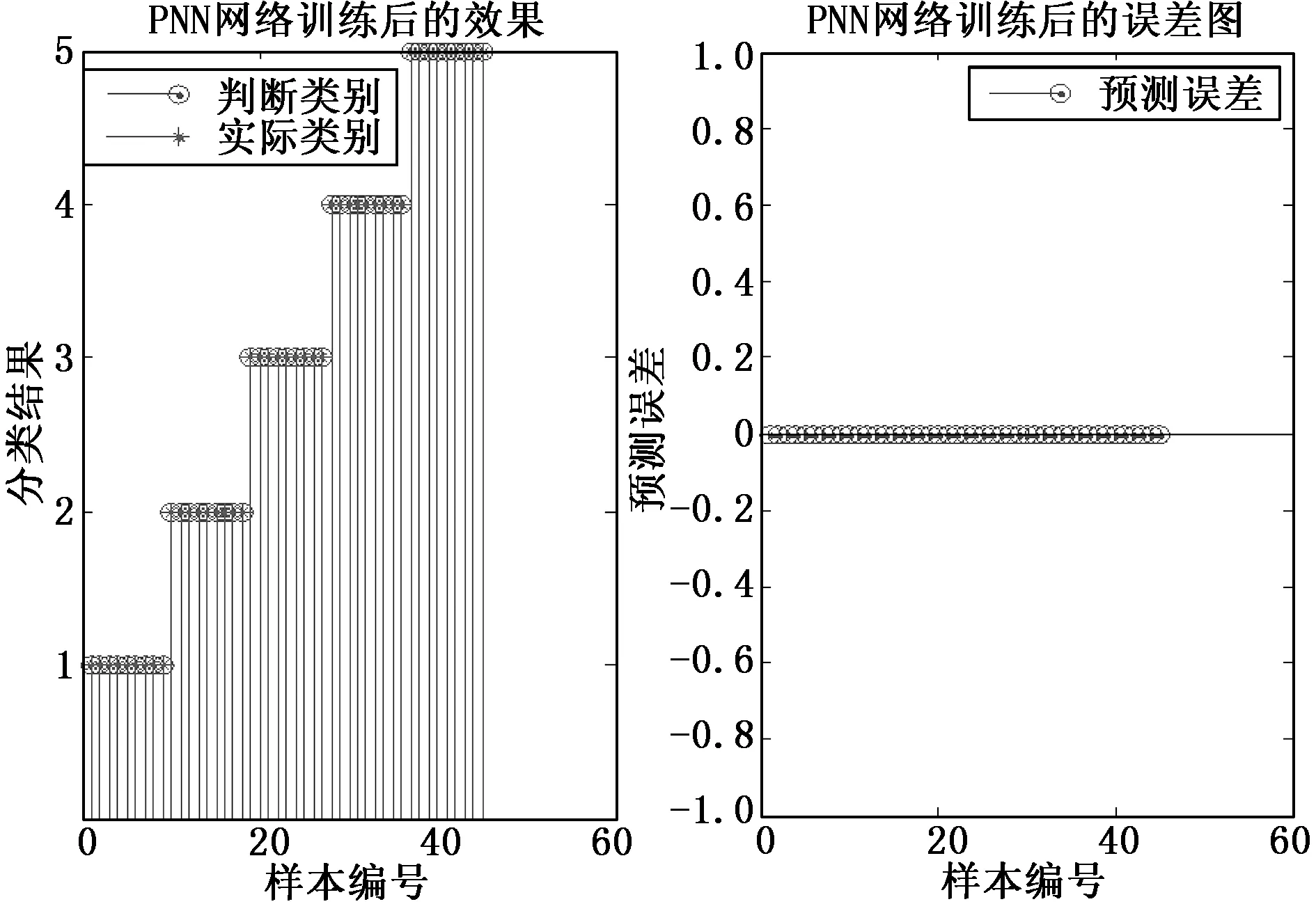
图4 PNN训练后的训练数据的分类效果图(压力调节器故障)

图4中的1、2、3、4、5分别与压力调节器的无故障、左前调节器故障、右前调节器故障、左后调节器故障、右后调节器故障5种故障类别相对应。从图4中可以看出，利用PNN进行故障诊断时，PNN网络输出的故障判断类别和故障的实际类别相同，诊断误差为0。

3.2.2 轮速传感器故障诊断模型的建立

针对轮速传感器的故障诊断，将2.5、3、3.5、4、4.5、4.7 s时所采集的数据作为训练样本。

在BP网络训练过程中，网络的构建函数、参数设置以及隐含层节点的设置范围与压力调节器相同。表4为隐含层节点在4～14范围内时，利用BP神经网络对轮速传感器进行故障诊断模型的训练结果。

表4 BP神经网络训练结果(轮速传感器故障)

从表4中可以看出，当隐含层节点数为6时，网络训练所得到的的均方根误差最小，其值为0.014 9，此时网络的平均绝对误差为0.055 7，训练时间为0.686 4 s，迭代次数为11次，此时网络训练过程的误差变化如图5所示。

图5 网络训练过程的误差变化(轮速传感器故障)

从图5中可以看出，当训练次数达到11步时，达到了预设的训练误差0.001，网络训练收敛。

在利用概率神经网络对轮速传感器进行故障诊断时，平滑因子的取值同样选取从0.1～10，间隔为0.1。训练结果发现当平滑因子取值为0.1～10时，网络训练的平均绝对误差都为0，但是当平滑因子取值为2.4时，训练时间最短为0.046 8 s，所以选择平滑因子的取值为2.4。和BP神经网络相比，BP神经网络的训练时间是PNN的14.7倍，PNN训练后训练数据的分类效果如图6所示。

图6 PNN训练后的训练数据分类效果(轮速传感器故障)

图6中的1、2、3、4、5分别与轮速传感器的无故障、左前轮传感器故障、右前轮传感器故障、左后轮传感器故障、右后轮传感器故障5种故障类别相对应。从图6中可以看出，针对轮速传感器的故障诊断，利用PNN进行故障诊断时，PNN网络输出的判断类别和故障的实际类别相同，诊断误差也为0。

对比BP神经网络发现，概率神经网络在压力调节器和传感器进行故障诊断时，模型的训练时间和训练精度都优于BP神经网络。

4 结果与分析

4.1 压力调节器的故障类别预测

将压力调节器故障在1.5 s时采集的样本数据作为测试样本，如表5所示。利用建好的基于PNN的压力调节器故障诊断模型对测试样本进行诊断(文中主要对测试样本的实际故障类别顺序为1-2-3-4-5和1-5-3-2-4时进行故障诊断)，诊断结果如图7和图8所示。

表5 压力调节器故障的测试样本

表6 传感器故障的测试样本

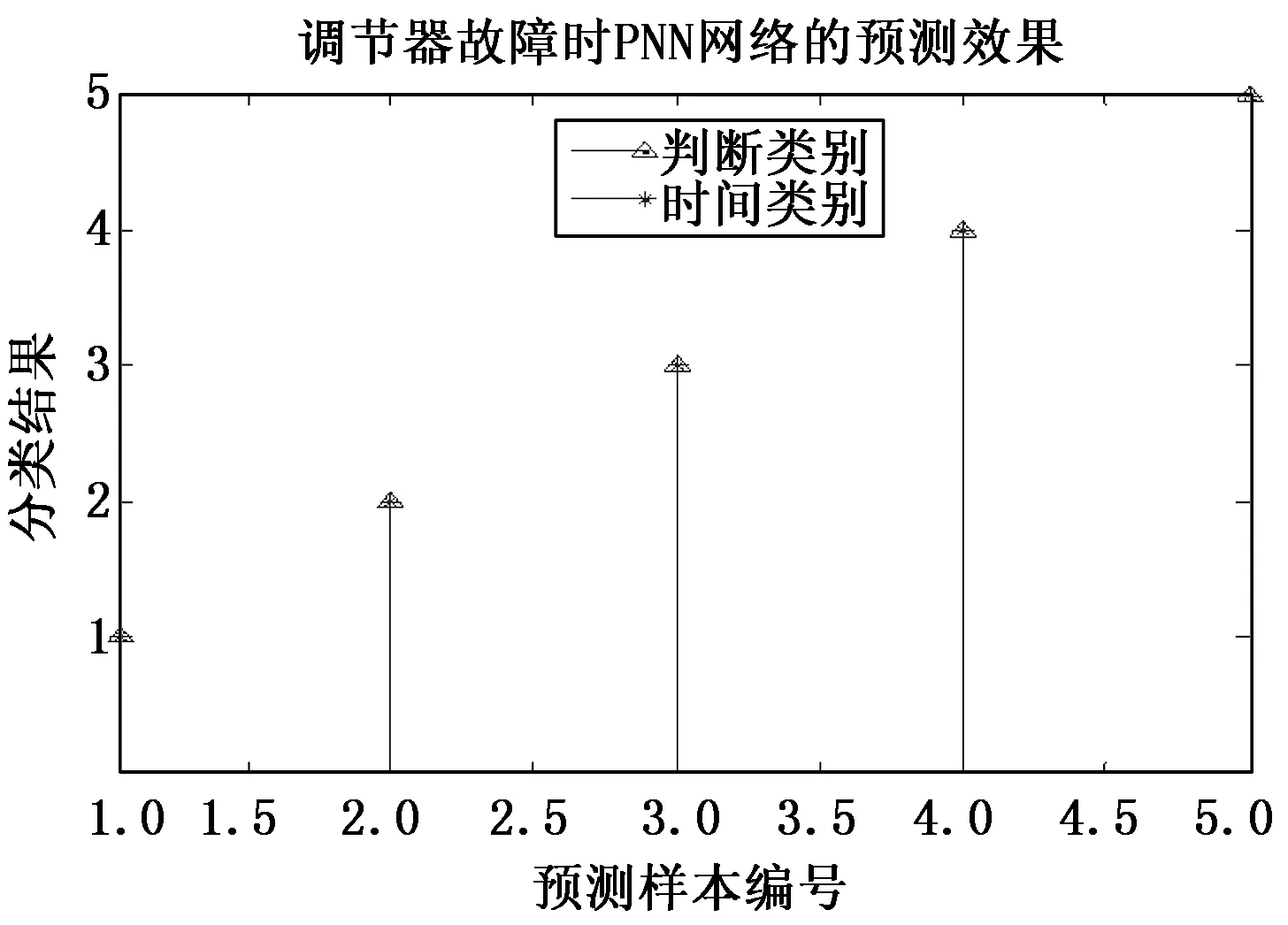
图7 PNN网络的预测效果(压力调节器故障的实际类别顺序为1-2-3-4-5)

结合7和图8可以看出，所建立的基于PNN的压力调节器故障诊断，无论测试顺序发生什么变化，PNN都能准确地进行故障诊断。

4.2 轮速传感器故障类别预测

将轮速传感器故障在2 s时采集的样本数据作为测试样本，如表6所示。利用建好的基于PNN的轮速传感器故障诊断模型对测试样本进行诊断(文中主要对测试样本的实际故障类别顺序为1-2-3-4-5和5-1-4-2-3时进行诊断)，诊断结果如图9和图10所示。

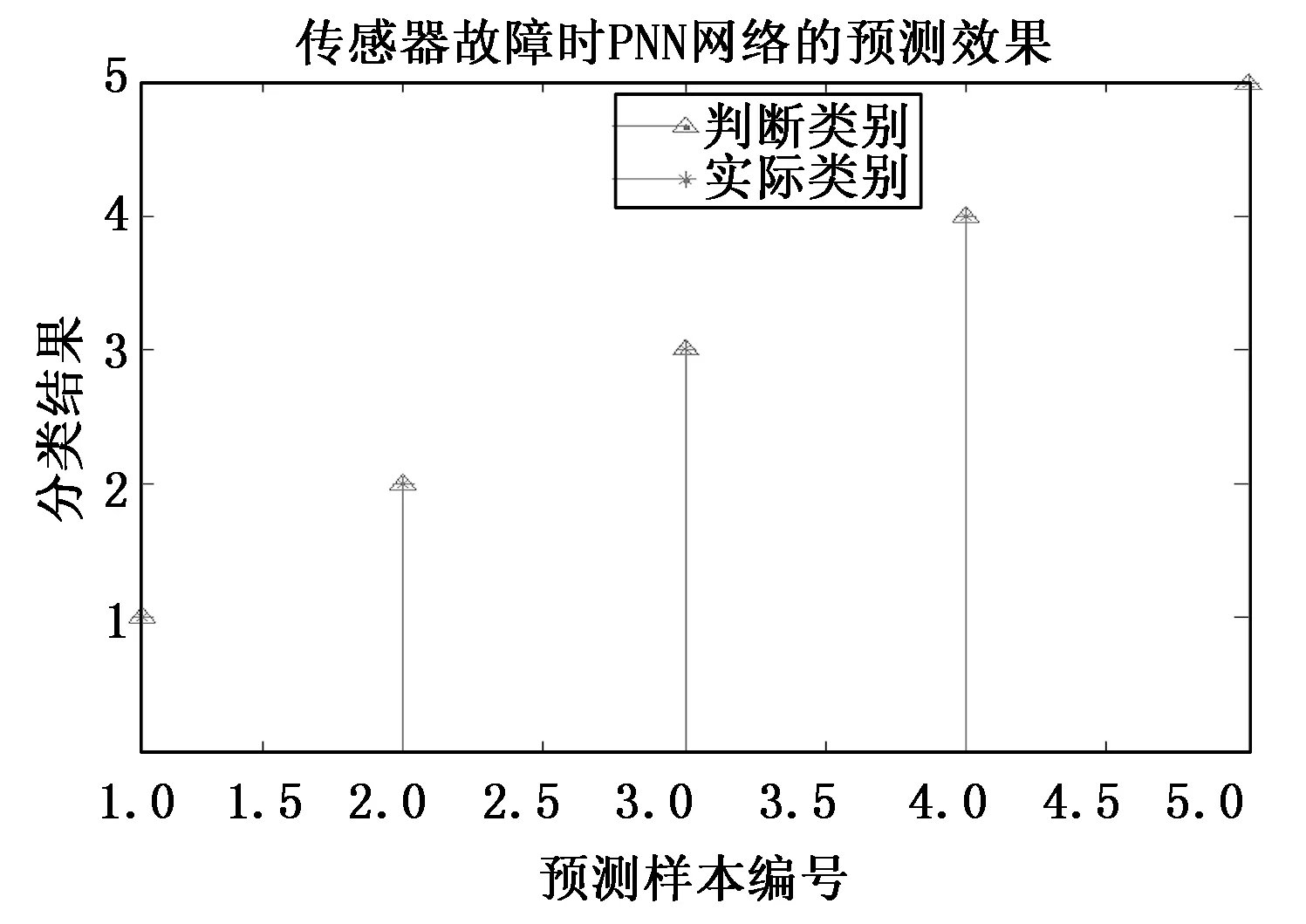
图9 PNN网络预测效果(轮速传感器故障的实际类别顺序为1-2-3-4-5)

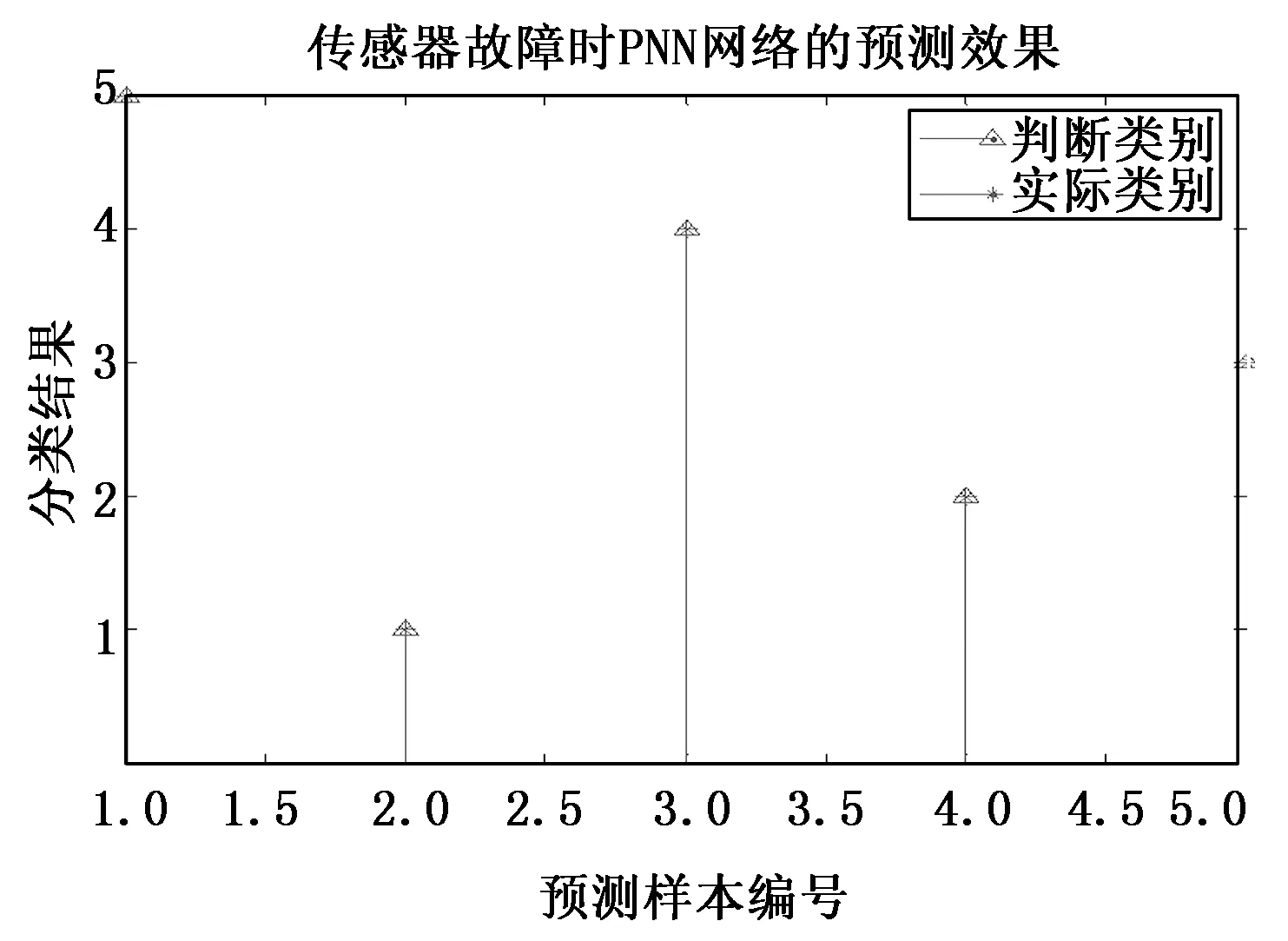
图10 PNN网络预测效果(轮速传感器故障的实际类别顺序为5-1-4-2-3)

结合图9和图10可以看出，无论故障诊断的测试顺序发生什么变化，所建立的基于PNN的轮速传感器故障诊断模型，都能准确地进行故障诊断。

5 结论

本文主要针对ABS系统的压力调节器和轮速传感器进行故障诊断。

1)利用相同的训练样本对PNN和BP神经网络进行训练。基于BP神经网络的压力调节器和轮速传感器的故障诊断模型的训练时间分别是基于概率神经网络的8.8和14.7倍。另外，从训练误差上来说，基于BP神经网络的压力调节器和轮速传感器的故障诊断模型训练的均方根误差分别为0.012 4和0.014 9，而基于PNN的压力调节器和轮速传感器的故障诊断模型的训练误差都为0。

2)利用测试样本集对基于PNN的压力调节器和轮速传感器模型进行检测，结果表明，无论压力调节器和轮速传感器实际故障类别顺序发生什么变化，基于PNN的故障诊断模型都能够准确的进行故障识别。