基于隔离防控策略下的新冠肺炎COVID-19传染模型

刘合财

(贵阳学院 数学与信息科学学院，贵州 贵阳 550005)

2019年末，湖北武汉开始出现了新型肺炎病例，病原体被确认为一种新型冠状病毒。世界卫生组织(WHO)将该新型冠状病毒命名为COVID-19(Corona Virus Disease 2019)。新型冠状病毒肺炎疫情的暴发引起全国及世界各国的高度重视，全国各地先后启动了重大突发公共卫生事件一级响应，可见此次疫情的严重性。科学有效地掌握疫情发展对于疫情防控至关重要，通过建立数学模型分析和预测疫情的发展趋势，为科学、有效的疫情防控提供参考，以便有关部门能及时采取措施,预防和控制传染病的蔓延。

传染病的传播规律,与人口研究的阻滞增长Logisitic模型的发展机理有相似之处。疫情往往遵循着期初潜伏孕育、萌芽缓慢增长、爆发快速增长以及终期衰退终结的阶段性过程。在自然状态下，感染者起初增加的速度逐步加快，当发展到一定程度后外界条件会施加阻滞作用，导致增加的速度会变慢，最终呈现出S型曲线。由于国家和人们对传染病的重视程度提高，往往还等不到自然条件的阻滞作用体现出来就已经采取了有力措施，数量增长的阻滞作用会比自然状态下提早呈现，并且措施越有力阻滞作用就越明显，疫情拐点就来得越早。

对传染病有关因素进行量化，从而可以建立描述传染病传播的经典数学模型：SIR模型、SEIR模型等[1]，主要思想是将人群划分为感染者、确诊者、隔离者、治愈者等，通过人群中某一群体转移至另一群体的传播学机制来建立常微分方程组并求解，从而揭示疫情传播规律。本文主要通过对新冠肺炎COVID-19疫情传染机理和统计数据的研究，绘制了疫情变化趋势图，建立了基于隔离防控策略下的SIR传染模型，为科学、有效的传染病疫情防控提供一些参考。

1 疫情趋势图

从国家卫生健康委员会官方网站收集全国31个省(自治区、直辖市)和新疆生产建设兵团报告的新型冠状病毒肺炎疫情数据，所统计的全国数据是从1月29日至3月11日每天公布的数据[2]。根据全国每天的新增确诊及疑似人数、累计确诊及疑似人数、治愈出院人数和死亡人数等数据，利用软件绘制出如下变化趋势图，从中反映出疫情变化趋势整体情况。趋势图反映了一定范围内疫情的严重程度、病毒危害程度，衡量疫情发展的总体态势。

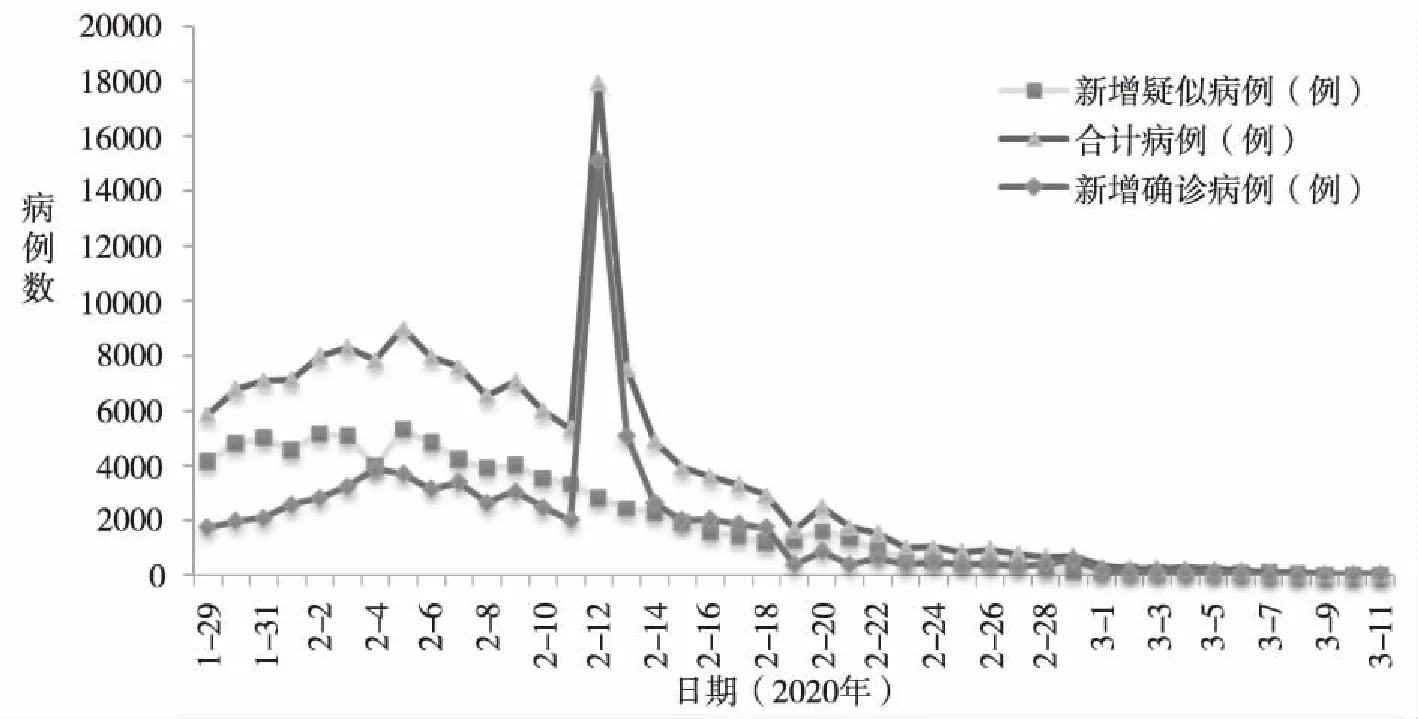
图1 COVID-19全国新增确诊及疑似病例数变化趋势图

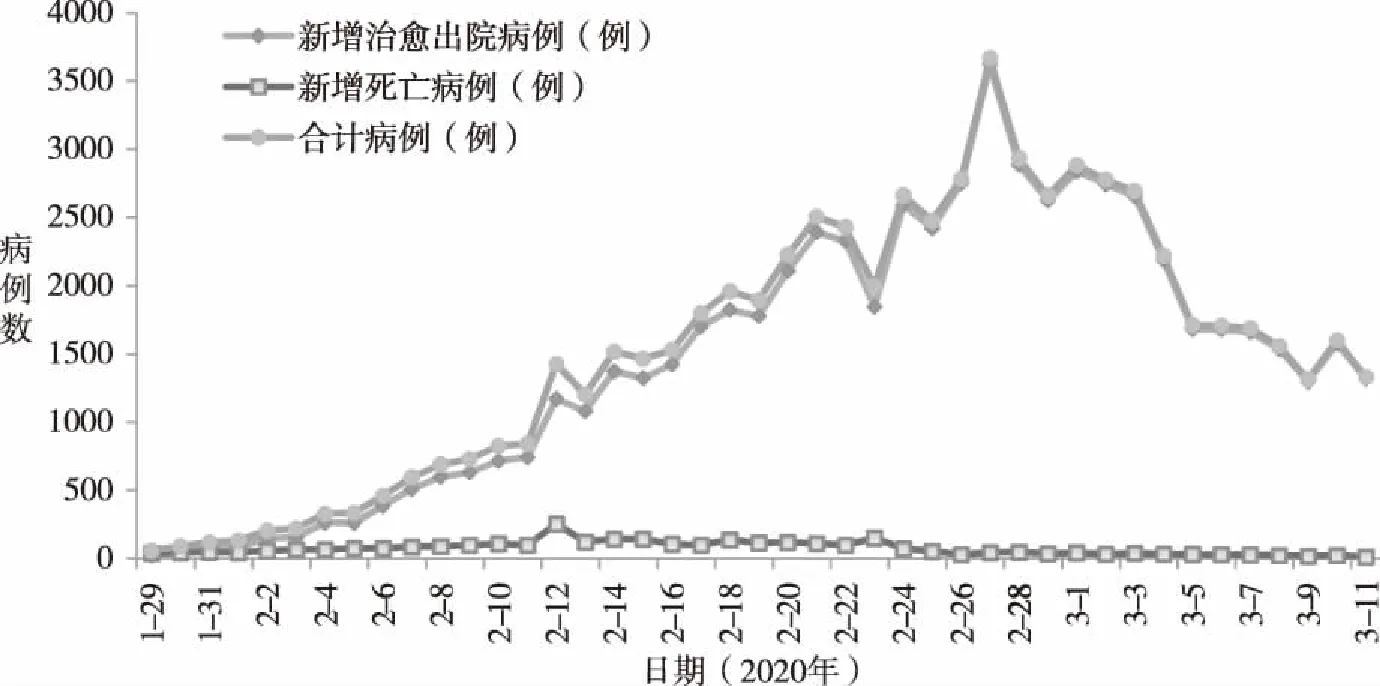
图2 COVID-19全国新增治愈及死亡病例数变化趋势图

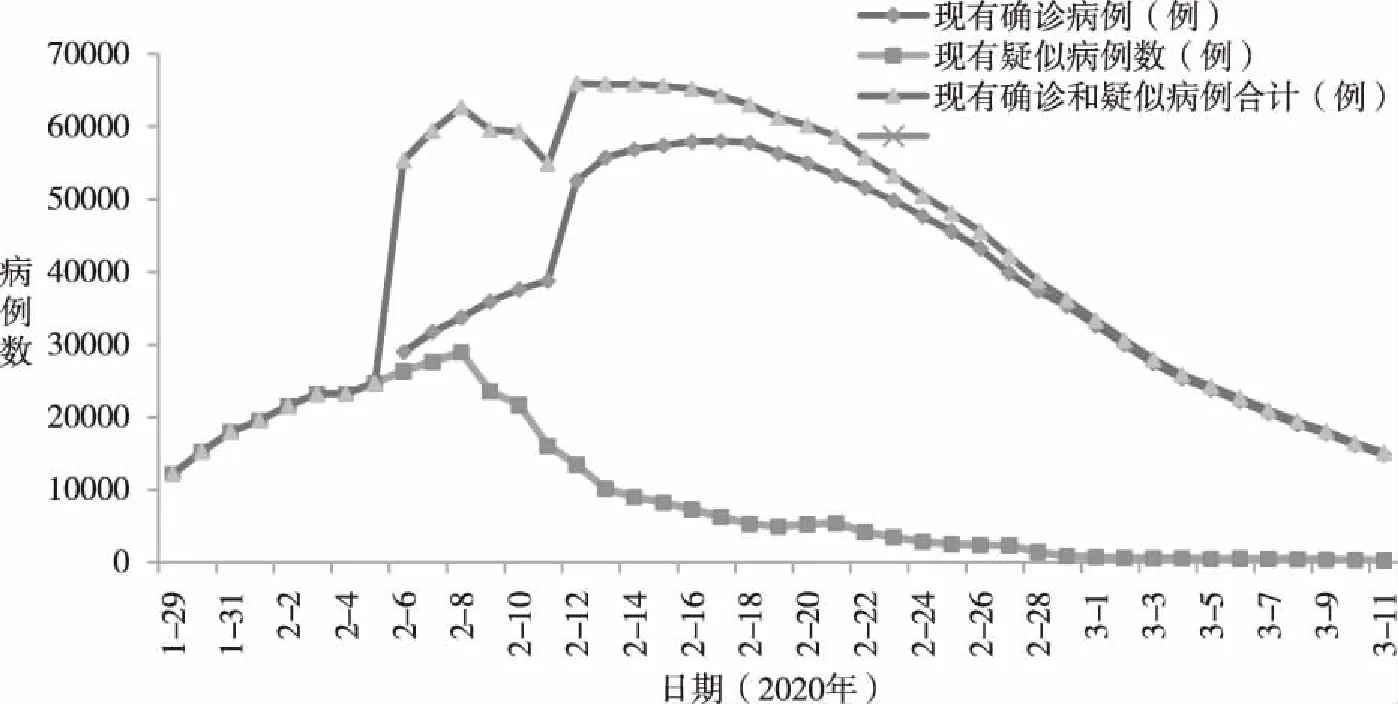
图3 COVID-19全国累计确诊及疑似病例数变化趋势图

图4 COVID-19全国累计报告确诊病例数变化趋势图

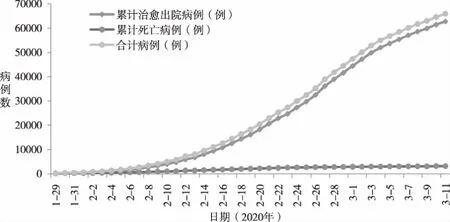
图5 COVID-19全国累计治愈及死亡病例数变化趋势图

2 隔离防控策略下的传染模型

2.1 SIR模型

将总人口群体划分为易感人群、感染人群、移出人群。易感人群(Susceptible，用S表示)是指那些尚未但很有可能被感染的个体群，感染人群(Infectious，用I表示)是指那些已感染且具有传染性的个体群，移出人群(Removed，用R表示)是指那些已感染过但不再具有传染性的个体群，不再具有传染性是因为被治愈或已死亡。

图6 SIR模型示意图

在流行病疫情的初期，易感人群的数量由于被传染将会逐渐减少，而感染人群的数量将逐步增长。随着感染人数的增长，易感者在传染病初期被感染的可能性将会逐步变大。当采取较强的控制措施以后，传染的速度会逐渐变慢，即单位时间内感染的人数会逐步减小，疫情最终会被完全控制而终结。

通常假设，单位时间内感染的数量与现有的感染者数量成正比，单位时间内治愈和死亡数量与现有感染者数量成正比。比例系数一般情形下可以假设为常数、时间的函数或分几段取常数。对于新冠肺炎，不计特殊病例，假设感染者被治愈恢复后不再被感染、不再复发，成为移出者。假设疫情期间人口的自然出生率和死亡率平衡，在隔离状态下一定时期内总人数基本保持不变。

时间用t表示，初始时刻为t0。S(t)为t时刻易感者的数量，I(t)为t时刻感染者的数量，R(t)为t时刻移出者的数量。k是单位时间内每个感染者感染的数量(传染率，传染系数),l是感染者的移出率(死亡率与治愈率之和)。受论文[1]等文献的启发，建立如下的SIR模型：

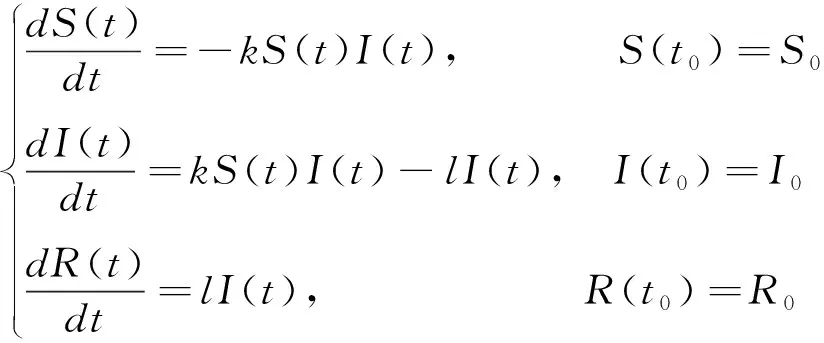
其中，S(t)+I(t)+R(t)=N,当人口用绝对数量计算时N为人口总数，用相对比例计算时N为单位1。

模型参数一般情形下可以是常数、分段常数或时间的函数，往往受防疫措施、医疗水平、免疫能力等因素影响，参数会在不同时间段取不同的值，但为了简化起见，本模型中传染率k、移出率l均视为常数。当病例信息缺失或者难以获取时参数拟合的效果会受到影响，可以根据国家卫生健康委员会每天公布的疫情数据进行统计分析，采取整体拟合参数得到参数的估计值。

2.2 隔离防控策略SIR模型

基于疫情的发展，武汉实行“封城”，全国各地也相继采取“封城”、“封路”、“封小区”、“封村”等隔离措施，全面实行公众居家隔离、集中隔离等。对于确诊病例、疑似人员的密切接触者等进行集中医学观察隔离。这一系列措施都属于隔离防控策略，在此策略下全国密切接触者人数大幅下降，病毒感染者逐步减少，疫情的严重程度相比于自由活动时已大幅减弱，取得了很好的效果。

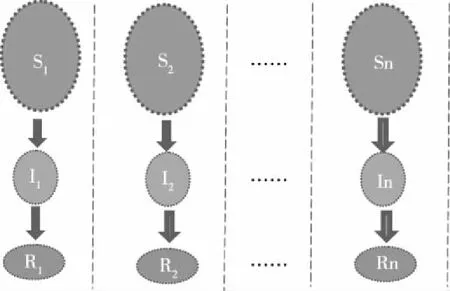
图7 隔离防控策略SIR模型示意图

将发生疫情的特定范围划分为n个相对隔离的系统，记第i个系统t时刻易感者的数量为Si(t)，感染者的数量为Ii(t)，移出者的数量为Ri(t)。记第i个隔离系统传染率为常数ki，移出率为常数li，Si(t)+Ii(t)+Ri(t)=Ni,N1+N2+……+Nn=N，当人口用绝对数量计算时N为人口总数，用相对比例计算时N为单位1。

于是，可得到如下隔离防控策略SIR模型：

i=1,2,3,……,n.

可根据数据确定模型初值和参数，再求出模型的解，从而进行疫情分析预测和判断。

3 结果与改进

本文所建立的模型揭示了传染病隔离防控策略的重要性，可为有关部门提供一些借鉴参考，由于统计数据和传播机理等方面的限制，如果能收集更多的疫情数据信息，可以提高预测的准确性。降低传染率k，增大移出率l(提高治愈率)，可以缩短传染病的病期。降低传染率，通过采取严格的隔离防控措施是做好COVID-19疫情防控的有效途径。而提高传染病治愈率依赖于研制新药、开创新疗法，提高医疗水平。

进一步研究可以从以下几个方面进行改进,包括建模、参数确定和预测。

(1)模型类型方面。除了建立连续型的传播预测模型外，还可以建立离散型的数学模型，比如差分递推模型。

(2)人群划分方面。对人群的划分，还可以进一步考虑加入潜伏者、隔离者、疑似病人、确诊病人、治愈者、留观者等更细的分类。有关资料表明，COVID-19的潜伏期通常在1至14天。考虑到传染病COVID-19存在潜伏期，假设在传染病流行的范围内，存在易感者、疑似者、感染者和移出者四类人群，建立SEIR模型更为契合新冠肺炎疫情的传播特征[3]。

(3)参数分段方面。可以考虑(隔离控制前、控制后)分阶段确定参数、参数是时间的函数(变量参数)。传染系数不但取决于控制措施的强弱，还与心理压力对免疫力的影响等因素有关，恐慌的心理对传染病有最可怕的影响，这一因素的量化会使模型更有效。

(4)分区域建模。考虑重点疫区，以其数据作为对象进行分析预测效果应该更为明显，全国的趋势很大程度上取决于重点疫区的发展趋势。

(5)基于统计发布数据的疫情拐点判断等相关问题。