基于图论的EMST聚类算法的适用性研究

魏 亮，陈晓耀，崔亚涛1，

(1.安徽中医药科学院 亳州中医药研究所，安徽 亳州 236800；2.亳州职业技术学院，安徽 亳州 236800；3.合肥工业大学，安徽 合肥 230009)

随着传统聚类分析方法在空间数据库中的应用，当前可用于空间聚类的算法非常丰富。然而，现有的空间聚类算法往往都具有其局限性，如何对当前的空间聚类算法进行归纳、整理，同时对其适用情况进行总结对于空间聚类分析的应用具有重要的意义[1]。

本文将通过对比实验，对EMST算法在空间数据库中的性能及适用性进行分析和总结。

1 EMST算法的理论基础

1.1 EMST算法的思想

EMST算法是基于图论的一种算法，能够探测不规则簇的界限。与传统的聚类算法不同，最小生成树聚类算法不假设球面形状基本数据。

图的最小生成树是所有生成树中边的权值之和最小的生成树。本文采用Prim算法构造最小生成树。如果从MST中删除一些边，就会产生一个连通分支的集合，则连通分支定义为簇。当一个簇中点的数量小于某个值的时候，作为噪声点处理。

1.2 EMST算法的描述

由于本文中的最小生成树方法建立在完全图的邻接矩阵基础上，因此，首先需构建一个包含所有聚类的赋权完全图G(V，E)，其中V为图的原始输入数据点集，E为图中各顶点间的边集，权值就是原始数据集各点间的距离，在得到各点间距离的邻接矩阵后，便可利用Prim算法查找最小生成树[2]。

基本思想是从源点S 开始构造树,然后每次在两个点的集合间(已在生成树上的点的集合Utree 与尚不在树上的点的集合Vtree) 选择一条最小代价边，随后将该边加入树中，并将相应端点加入集合Tree 中，最终当V中所有点均在集合Tree 中时，最小生成树算法结束[3]。

下一步是删除不一致边，当满足 |m-l|〉qσ(m 代笔所有边的平均值，l代表每条边的值，q是固定值，σ是标准差)条件时，删掉此边。每删掉一条边，就标记一个簇，如果簇的数量小于2，就作为噪声点。

1.3 EMST算法的流程

EMST算法的流程：

(1) 加载数据图层

(2) 求邻接矩阵

(3) prim法求最小生成树

(4) 删掉最小生成树中不一致边

(5) 标记簇

(6) 用不同的几何符号和颜色显示结果

2 EMST算法对比实验

为了进一步说明EMST算法的性能及适用性，本实验共设计了九个模拟实验数据进行对比分析。本节设计的九个模拟实验从以下四方面：(1)簇的空间形态(类球形和任意形状)；(2)簇的空间密度差异；(3)簇的空间邻近；(4)噪声点(孤立点)的影响来比较EMST算法的优缺点，同时对EMST算法参数的不同取值分别计算聚类结果，探讨参数对其聚类结果的影响[4-10]。

对于EMST算法，删除不一致边的条件是|m-l|〉qσ，本实验中对参数q取三次不同的值进行对比实验。

2.1 模拟实验一

第一个模拟实验共有254个点，是密度分布比较均匀的类球形簇，图1是EMST算法针对密度分布比较均匀的类球形簇的运行结果：

图1 EMST算法的运行结果

从算法的聚类结果可以看出，参数取不同值时，三副图聚类效果一样，说明了对于此数据，参数对EMST算法影响很小，同时也验证了此算法适用于密度分布均匀的类球形簇。

2.2 模拟实验二

第二个模拟实验共有263个点，在第一个模拟实验数据的基础上增加了若干噪声点，图2是EMST算法针对带有噪声点且密度分布比较均匀的类球形簇的运行结果：

图2 EMST算法的运行结果

从算法的聚类结果可以看出，随着参数的增大，每个类的成员有增加的趋势。对于此数据，当参数q =1.645时，聚类效果最好，q=2的时候比较好。说明EMST算法对于带有噪声点且密度分布比较均匀的类球形簇，EMST算法处理效果非常好。

2.3 模拟实验三

第三个模拟实验共有280个点，是密度分布比较均匀的任意形状簇，图3是EMST算法针对密度分布比较均匀的任意形状簇的运行结果：

图3 EMST算法的运行结果

从算法的聚类结果可以看出，对于密度分布比较均匀的任意形状簇，EMST算法聚类效果很好，并且EMST算法受参数影响不大，三幅图聚类结果都正确。

2.4 模拟实验四

第四个模拟实验共有293个点，在第三个模拟实验数据基础上增加了若干噪声点，图4是EMST算法针对带有噪声点且密度分布比较均匀的任意形状簇的运行结果：

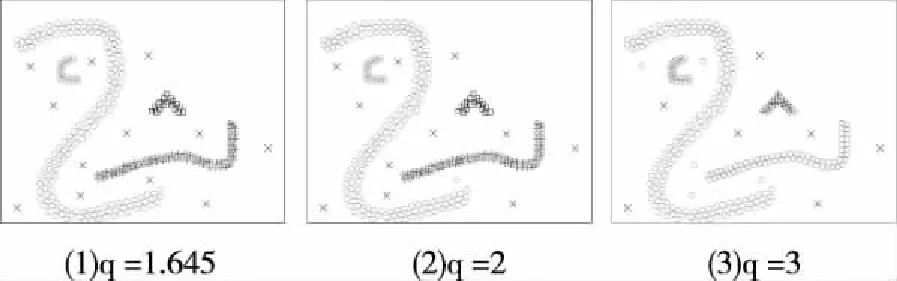
图4 EMST算法的运行结果

从算法的聚类结果可以看出，当参数q=1.645时聚类效果最佳，q=2时效果较好。说明对于带有噪声点且密度分布比较均匀的任意形状簇，EMST算法处理效果非常好。

2.5 模拟实验五

第五个模拟实验共有245个点，是密度分布差异较大的任意形状簇，图5是EMST算法针对密度分布差异较大的任意形状簇的运行结果：

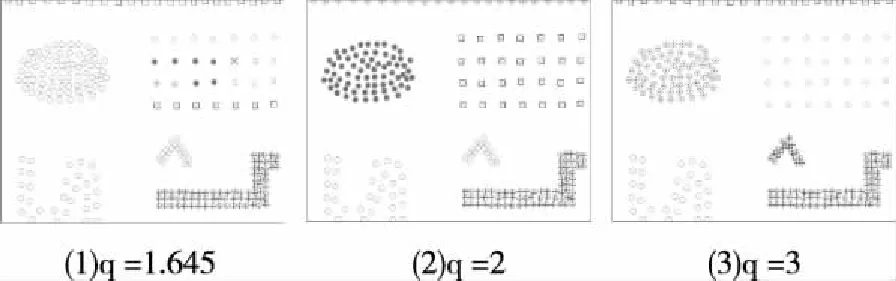
图5 EMST算法的运行结果

从算法的聚类结果可以看出，只有图(2)的聚类效果最好，说明EMST算法中当参数取值为2的时候能够发现正确的簇，此法适用于密度分布差异较大的任意形状簇。

2.6 模拟实验六

第六个模拟实验共有254个点，在第五个模拟实验数据的基础上增加了若干个噪声点，图6是EMST算法针对带有噪声点且密度分布差异较大的任意形状簇的运行结果：

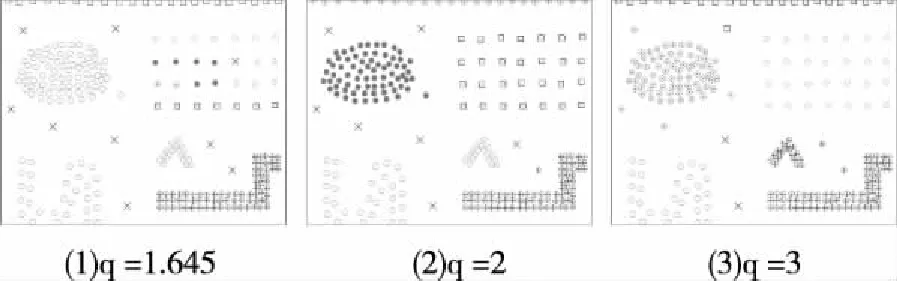
图6 EMST算法的运行结果

从算法的聚类结果可以看出，只有图(2)的聚类效果相对较好，说明EMST算法中当参数取值为2的时候，能够发现噪声点，此法比较适用于带有噪声点且密度分布差异较大的任意形状簇。

2.7 模拟实验七

第七个模拟实验共有241个点，是分布密度差异较大并有相邻情况的任意形状簇，图7是EMST算法针对密度分布差异较大并有相邻情况的任意形状簇的运行结果：

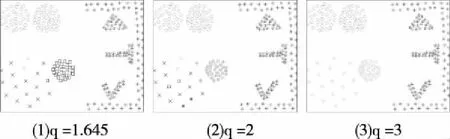
图7 EMST算法的运行结果

从算法的聚类结果可以看出，当参数取的小时，一些分布有规律的点被当做了噪声点来处理，而参数稍大一点，一些分布规律明显不同的簇被聚为一类。说明EMST算法对密度分布差异较大并有相邻情况的任意形状簇的处理效果差。

2.8 模拟实验八

第八个模拟实验共有258个点，在第七个模拟实验数据的基础上增加了若干个噪声点，图8是EMST算法针对带有噪声点且密度分布差异较大并有相邻情况的任意形状簇的运行结果：

图8 EMST算法的运行结果

从算法的聚类结果可以看出，对带有噪声点且密度分布差异较大并有相邻情况的任意形状簇，EMST算法并不适用。

2.9 模拟实验九

EMST算法适合于类球形簇，所以第九组模拟实验是类球形兼有空间邻近和密度分布不均匀的簇，继续验证其算法的适用性。图9是EMST算法针密度分布差异较大并有相邻情况的类球形簇的运行结果：

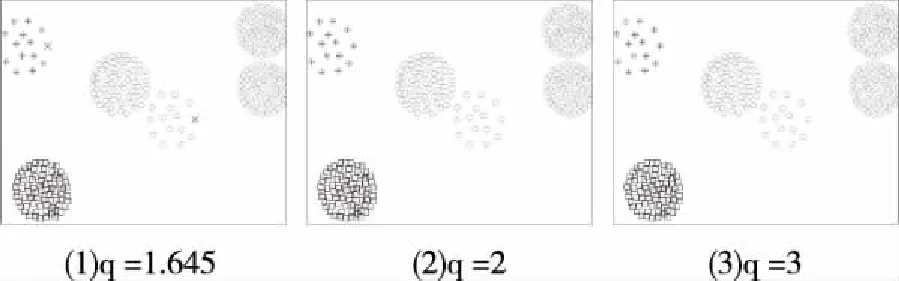
图9 EMST算法的运行结果

从算法的聚类结果可以看出，对密度分布差异较大并有相邻情况的类球形簇,EMST算法并不适用。

3 结论

对EMST算法进行了对比实验测试，将参数q在不同取值时所对应的聚类结果进行比较，并且进一步比较了四种干扰因素(簇的空间形态、簇的空间密度差异、簇的空间邻近、噪声点的影响)对聚类结果的影响，从而确定EMST算法在空间数据库中的性能。

通过对EMST算法进行的实验对比，总结出该算法的适用性：(1)空间簇的邻接对其影响较大，对发现相邻簇的效果不好，空间密度的差异对其结果具有一定的影响。(2)能发现任意形状的簇，可以发现比较明显的噪声点。q比较小时，密度比较稀疏的簇被当做噪声点，q比较大时，不同的簇被归为一类，q的取值为2左右的效果比较好。

EMST算法的该种特性，可以成为是否选用该算法进行空间聚类的决定指标，也进一步增强了该算法的实际应用价值。