非线性非自制系统的Lyapunov稳定性

席 敏

(贵州大学 大数据于信息工程学院，贵州 贵阳 550025)

一个自动系统要能正常工作，必须是一个稳定的系统。因此，对于一个系统来说，研究稳定性是很有意义的。所谓稳定性指的就是当系统受到外界干扰后，显然它的平衡被破坏，但在外扰消失以后，它仍有能力恢复或者接近原来的状态工作。非线性系统指的就是系统不满足齐次性和可加性，即不满足叠加性的系统。而非自治系统指的就是系统与时间相关，系统是时变的。在实际工程中遇到的一些系统是非线性非自治的，因此研究非线性非自制系统的稳定性具有重要意义。

对于非自治系统判断其全局一致渐近稳定以及全局渐近稳定的方法主要是运用Lyapunov构造能量函数法，即第二方法，但其分析系统平衡点的稳定性只是充分条件，因此，本文主要引出K类函数来增加条件，由此将能量函数寻找的范围缩小。

1 非线性非自制系统的定义及其稳定性的判定定理

设非线性非自制系统的方程为：

(1)

(2)

设函数满足||f(t,x)-f(t,y)||≤L||x-y||(L>0)是满足Lipschitzt条件的，且函数是逐段连续的。由此(1)的解唯一。

1.1 相关定义

定义2定义系统

设D为原点的某个领域，如果对于任何x∈D，当x≠0时，有标量函数V(x)>0且V(0)=0，则称V(x)为正定函数。

定义4K类函数

一个连续函数l(t)：l(t):[0,l)→[0,∞)[0,l]称之为K类函数，满足

(1)该函数是严格递增函数；(2)该函数满足l(0)=0.

1.2 稳定性判定定理

Lyapunov研究运动稳定有两种方法，即第一方法和第二方法。第一方法是将非线性系统在平衡状态附近线性化，然后通过讨论线性化系统的特征值或者极点分布及稳定性来讨论原来系统的稳定性问题。第二方法是定义一个能量函数V和根据扰动方程的计算直接判断稳定性[1]，第二方法相较第一方法运用的更广，是研究稳定性的主要方法。

(1)V(x)是正定的，V(0)=0;

笔者认为乡村旅游的可持续发展重点在于游客对目的地的依恋与重游，持续不断的市场需求是其发展的源泉与动力，关键在于乡愁情怀的培育与维护。“乡”本是一个地理概念，更是乡愁的物质载体，根植于人的内心，在特定的时间空间条件下产生特定的记忆，凝聚一个地方的生活，是对文化认同的情感投射，更是返璞归真的心灵慰藉[10]15。从乡愁到乡居最后到乡思的情感依恋造就了乡村旅游的灵魂，推动着乡村旅游的可持续发展。

Ⅰ：k1·||x||p≤V(t,x)≤k2||x||p

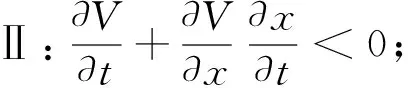
Ⅰ：

L1(||x||)≤V(t,x)≤L2(||x||)

L1(•)，L2(•)是K类函数，对于所有(∀x∈Rn,∀t≥0)都成立。

L3(•)为K类函数，对于所有x∈Rn,∀t≥0都成立。则系统的原点平衡状态为全局渐近稳定。

2 总结

本文对运用Lyapunov函数第二法对非线性非自治系统的稳定性进行判定，但Lyapunov第二法分析系统稳定在实际过程中有很大的难度，因为Lyapunov函数是很难找到的。由此本文引出K类函数，将能量函数的构造难度减小。