关于可解群是超可解群的一个结论
2020-04-28曾利江
曾利江
(遵义师范学院 黔北文化与经济研究院,贵州 遵义 563006)
有限群的性质是极其丰富的,众所周知,它在各个自然科学中起到了极其重要的作用,本文将讨论满足一定条件的一类可解群是超可解群的这一重要结论。
群G为幂零的充要条件是G的每个极大子群在G内正规[1-5]。将“正规”改为“拟正规”,“极大”改为“2-极大”,也可得到关于超可解群的类似结论,借助于次正规子群的性质[6-8],证明了当2-极大子群均为拟正规时,群G是超可解的,当群G的阶的素因子个数不小于3时,群G还是幂零的。当然,这些术语下面都要给予确切的定义。
1 定义及其讨论
定义1群G之子群H若与G的每个Sylow子群Gp可交换(即HGp=GpH),就叫H为G的拟正规子群。
引理1设H为G的拟正规子群。于是
(1)若θ为G的同态映射,则Hθ为Gθ的拟正规子群;
(2)G≥K≥H,则H也是K的拟正规子群。
证明(1)令N=kerθ,则Gθ≅G/N,于是若ψ∈Sylp(Gθ),则因P∈Sylp(G)时⟹PN/N∈Sylp(G/N),故有τ∈Sylp(Gθ)使得在同构关系Gθ≅G/N中有τ≅PN/N,然而因为存在gθ∈Gθ使得ψ=τgθ=(gθ)-1τgθ,而在同构关系Gθ≅G/N中有gθ↔gN故又得同构对应
τgθ≅(PN/N)gN=PgN/N=SN/N,
使得有S=Pg∈Sylp(G),即ψ≅SN/N,因而Sθ≅SN/N说明了ψ=Sθ,即Gθ的任意Sylow子群可视为G的某Sylow子群S的象Sθ。
因H拟正规于G⟹HS=SH,故(HS)θ=(SH)θ⟹HθSθ=SθHθ,说明Hθ与Gθ的任何西洛子群Sθ可交换,故Hθ拟正规于Gθ。
(2)再令S1∈Sylp(K),由Sylow理论知∃S∈Sylp(G)使得S1≤S,故S1≤K∩S,但K∩S又为K之一个p-子群,于是有S1=K∩S。然而H拟正规于G⟹HS为G的子群,故K∩HS=H(K∩S)=HS1为K的子群,因而HS1=S1H,说明H是K的拟正规子群。
引理2设G是可解群,而H是G的拟正规子群,那么H/HG是幂零群。
附注HG=∩{x-1Hx|x∈G},即为G中所有与H共轭的子群x-1Hx(x取遍G)之交。
证明G▯G/HG⟹H/HG为G/HG的拟正规子群(引理1(1))。于是当HG≠1时,令
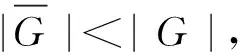
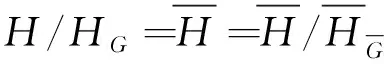
于是今后只需考虑HG=1的情况。这时要证明H为幂零群。
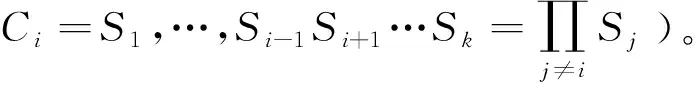
(a)若R∈Sylpi(H)且x∈Ci,则必Rx≤H。
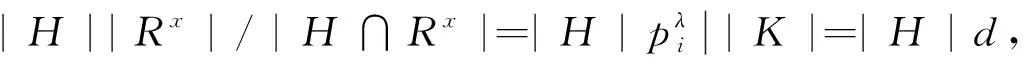
(b)当pi≠pj时,HSi∩HSj=H。
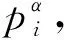
(c)对每个pi而言,H∩Si∈Sylpi(H)。
|H∶H∩Si|=|HSi∶Si|说明|H∶H∩Si|与pi互素,但H∩Si又为H的pi-子群,故H∩Si∈Sylpi(H)。
为了证明H的幂零性,只需每个H∩Si◁H能被解决即可。于是只需证明每个x∈H∩Si与每个y∈H∩Sj可交换,即xy=yx。
因为已假定了HG=1,故只需证[x,y]=x-1y-1xy∈HG。∀g∈G=CiSi⟹g=γσ(γ∈Ci,σ∈Si),故g-1[x,y]g=σ-1(γ-1x-1γ)(γ-1y-1xyγ)σ。因H∩Si与y-1(H∩Si)y都是H的Sylowpi-子群,故γ-1x-1γ∈H及γ-1y-1xyγ∈H(利用了(a)),于是,g-1[x,y]g∈SiHHSi=HSi。同理,g∈G=CjSj⟹g-1[x,y]g∈HSj。因此有g-1[x,y]g∈HSi∩HSj=H(参见(b)),即[x,y]∈gHg-1,故由g的任意性有[x,y]∈HG。
引理3设G是可解群,而H为G的拟正规子群,那未H在G内是次正规的。
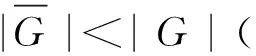
当Si∈Sylpi(G)时,注意H∩Si∈Sylpi(H)(因为[H∶H∩Si]=[HSi∶Si]),故从H的幂零性可知H∩Si◁H,即H有唯一个Sylowpi-子群。于是∀Pi∈Sylpi(G),由于H∩Pi∈Sylpi(H)有H∩Si=H∩Pi≤Pi,说明H的唯一个Sylowpi-子群是G的每个Sylowpi-子群的子群。故应有H∩Si≤Opi(G),从而H∩Si≤Fit(G),即幂零群H的任何Sylow子群都是Fit(G)的子群,因之得H≤Fit(G),于是从Fit(G)的幂零性可知H为Fit(G)的次正规子群,故再由Fit(G)◁G得H次正规于G。
引理4设H为可解群G之拟正规子群。若H是G的极大子群,则H◁G。
证明H拟正规于G⟹H次正规于G,故有G的子群列
H=K0 使每个Ki◁Ki+1。然而H在G内的极大性说明在H与G之间再不能插进真包含H的G之真子群,故必t=1,即H=K0 定义2如果H是群G的某极大子群M的极大子群,就把H叫做G的2-极大子群。也就是说在关系式H 定理1设可解群G的每个2- 极大子群在G内是拟正规的,那么G是超可解群。若这时|G|含有3个或更多个不同的素因数,G还是幂零群。 证明令|G|之素因数分解为 就P1来说,有G的子群列如: H0=P1 由上面的推导证明中可以看出,引入拟正规子群的定义后,可以深入挖掘出一系列的性质,2-极大子群的条件不是很苛刻,借助现存的次正规子群的性质,就可以证明2-极大子群很好的性质,不仅和超可解群联系起来,还在群的阶指数不小于3的多数情况下,和幂零群联系起来。2 定义及主要结论
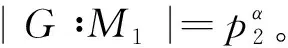
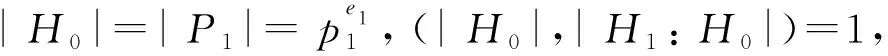
3 结语
