卫星定位轨迹最小二乘拟合适应性分析

陈志强，鲍鹏宇，宁云转

(北京全路通信信号研究设计院集团有限公司，北京 100070)

北斗卫星导航系统是中国自行研制的全球卫星导航系统，可实现与其他国家的卫星定位系统兼容共用，为用户进行全天候、全天时的定位服务。随着北斗三号基本系统的建设完成，北斗系统的服务范围从区域扩展到了全球。近年来卫星定位系统快速发展，世界各国先后开展了基于卫星定位技术的列控系统研发工作，美国通用电气研发的增强型列车控制系统（Incremental Train Control System，ITCS）已经在我国青藏铁路稳定运营十余年[1-5]。轨道的地理坐标信息是基于卫星定位列控系统的基础数据，目前常用的获取轨道位置的方法包括人工定点采集和曲线拟合两种方法[6-7]。由于定点采集具有效率低下和容易出现采集错误的问题，因此本文对基于最小二乘方法的轨道卫星定位轨迹拟合方法展开研究和讨论。

1 最小二乘轨道拟合方法

如图1 所示，装有卫星接收装置的列车从A 点运行到B 点，途中实时接收列车的卫星信息。经过多次往返，采集到轨道的定位数据，通过最小二乘拟合的方式实现轨道定位信息的采集，此方法具有方便快捷，实施简单的特点。

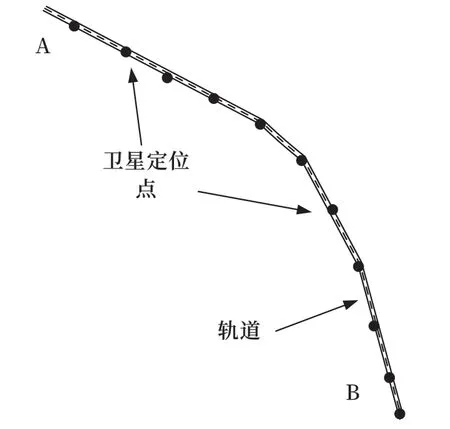
图1 卫星定位轨迹拟合示意图Fig.1 Schematic diagram of satellite positioning trajectory fitting

2 最小二乘拟合算法

最小二乘拟合是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小[8]。

待拟合点为 (xi,yi)，其中。欲对这些点进行最小二乘拟合，可以建立方程如公式（1）所示[9]。

显然，该方程组一般而言没有解，为获取最优解，引入最小二乘问题的矩阵形式：

最小化f(a) ：

可得到最小二乘问题的最优解：

由于列车轨道具有转弯半径大，大多数轨道平直的特点，可对公式（1）进行简化，令公式（1）的参数m 为2，获得待拟合点的线性拟合数据。

3 经纬度最小二乘拟合问题分析

经纬度坐标是基于地理坐标系描述的卫星定位原始数据。基于此描述的各点处于球面上，其进行最小二乘拟合时存在2 个问题。

1)球面两点之间的距离不能使用经纬度差的2范数直接进行描述。公式（2）～（4）所描述的最小二乘方法的优化结果并非最优解。

2)经纬度坐标与平面坐标系是非线性映射的，地理坐标系的线性最小二乘的直线映射到平面坐标系后会变为曲线。

针对上面两个问题，需要对最小二乘拟合在地理坐标系中使用的适应性进行分析。

3.1 经纬度坐标距离分析

如图2 所示，A、B、C、D 为地球表面上的点，线段AD 和BC 上所有的点分别有相同的经度，线段AC 和BD 上的点分别有相同的纬度。A、B 两点的经纬度坐标分别为(a1, β1)和 (a2, β2)。

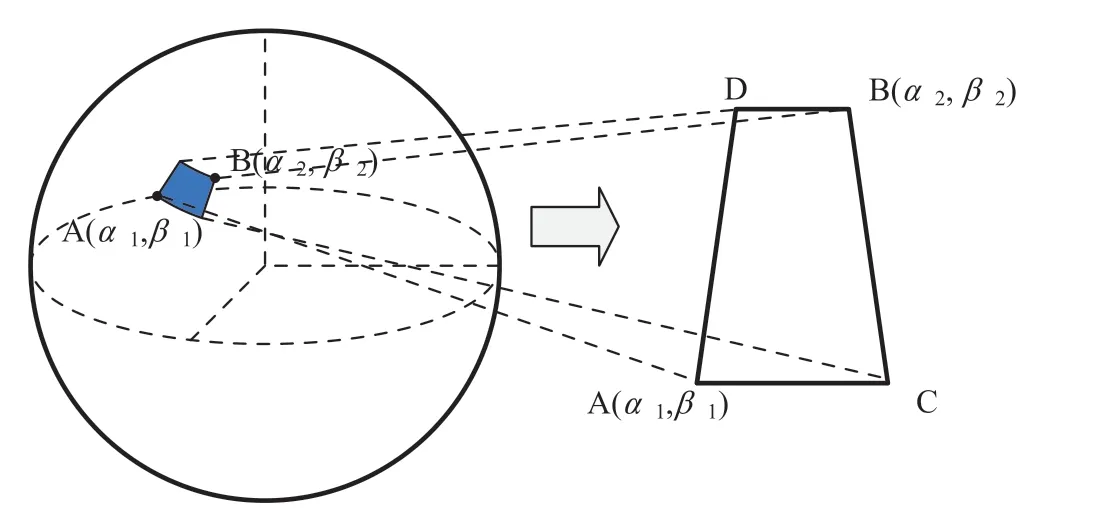
图2 经纬度坐标与平面直角坐标映射图Fig.2 Map of latitude and longitude coordinates and plane rectangular coordinates

为分析最小二乘的适应性问题，不失一般性，可简化坐标系映射关系。设地理坐标系原点为东经0 度，北纬0 度，则存在某点的坐标为 (a, β)（单位：度），则该点映射到平面坐标系的坐标为(x, y)，其映射关系为：

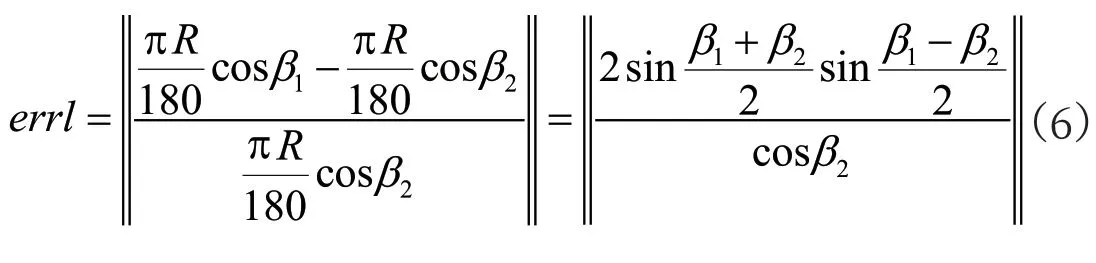
假设1：A、B 两点距离很近，公式（6）可化简为：

根据公式（7）可知，线性误差受到两个因素的影响：

2)两坐标点纬度的正切值tanβ2。

根据上述两个因素可知，若控制errl 小于e，则需要满足假设2。

引理1：两坐标点2 范数距离误差小于其中一个坐标变量之差的误差。

证明：

设两坐标点为(x1, y1)和 (x2, y2)，其2 范数距离为，其中a=x1-x2，b=y1-y2。

根据误差传递公式， a 的误差对l 影响为

因此，有Δl≤ Δa。

同理，有 Δl≤ Δb。

证毕。

综上，根据引理1，在满足假设1 和假设2的情况下，可确保两坐标点的距离误差小于e，从而最小二乘的解为其在误差e 控制范围内的近似最优解。

3.2 经纬度坐标拟合线性分析

待拟合卫星定位点为(αi, βi)，其中。应用公式（1），并取公式（1）的m 为2，对待拟合点进行最小二乘拟合，可以建立方程如公式（12）所示。

其最小二乘最优解为：

为分析地理坐标系与平面坐标系的线性对应关系，需将使用公式（5）代入到公式（1）的参数K和Y 中。

将公式（5）代入最小二乘方法公式（1）的系数K 中，并取公式（1）的m 为2，可得到：

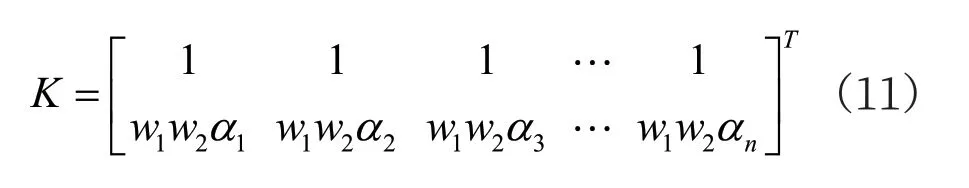
对公式（11）进行简化，有：

将公式（5）代入最小二乘方法公式（1）的Y中，可得到：

对公式（13）进行简化，有：

将公式（12）和（14）代入到最小二乘最优解公式（4）中，得到经纬度坐标点对应平面坐标系下的最小二乘最优解：

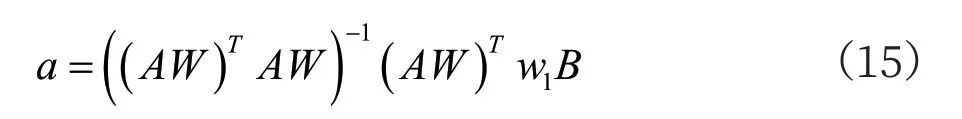
经化简可得到：

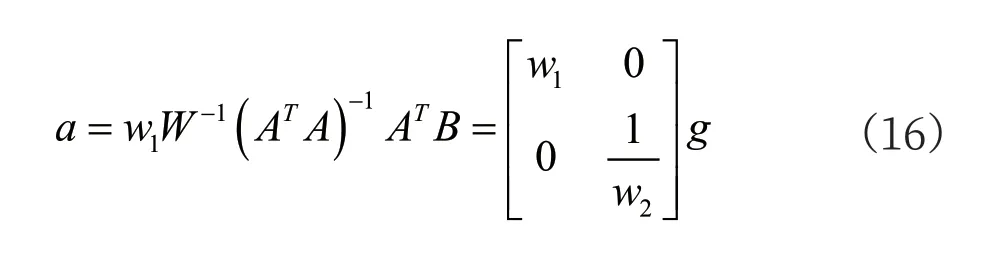
其中，a 和g 分别为平面坐标系和地理坐标系的最小二乘线性拟合最优解。

由此可见，地理坐标系的最优解g=[g0, g1]和平面坐标系的最优解a=[a0, a1]存在一一对应关系。

假设3：假设待拟合点距离很近，其最大与最小经度的余弦值之差小于errβ。

在满足假设3 的情况下，系数w1和w2均为恒定值，待拟合卫星定位点的最小二乘线性拟合结果 β=g0+g1α 与其在平面坐标系上的映射均为直线，且可经过旋转和平移得到。

4 结论

本文针对人工采集轨道卫星定位数据存在的问题，提出一种轨道数据最小二乘拟合方法。并针对地理坐标系和平面坐标系的特点，对最小二乘的应用条件进行了分析，提出3 个假设。在满足3 个假设的情况下，可直接使用最小二乘方法对经纬度坐标进行线性拟合，拟合结果与其在平面坐标系上的映射具有一一对应的线性关系。使用该拟合结果可得到轨道地理信息的近似最优解。本文提出的最小二乘拟合方法可实现轨道的实时运算，提高了拟合效率和轨道数据的可靠性，为轨道信息的采集提供了一种切实可行的方法和理论依据。