计算教学渗透建模思想的时机

徐宏臻　陆兆芬

《义务教育数学课程标准（2011年版）》特别注重发展学生的模型思想，将其作为十大核心概念之一而明确地提了出来。计算是小学数学重要的教学内容，蕴涵着明确的建模思想，而建模思想需要学生在“做”的过程和“思”的过程中慢慢积淀，在数学学习活动中逐步感悟。为此，教师要高度重视数学建模，心中有强烈的建模意识;要精心设计有价值的教学活动，做实、做好教学过程，让学生充分进行“再创造”“再发现”;要重视回顾和反思，让学生在有效的数学活动中逐步感悟和体验建模思想;要让学生适当尝试建模，在计算时建构新的模型。现结合具体课例，谈谈如何在整数计算教学中渗透建模思想。

一、备课时领悟建模思想

教材往往是按建模的过程编写的，即先把生活问题转化为数学问题，再用数学方法加以解决，并检验和评价结果的意义，从中得到一般化的算法，最后加以推广和运用，以解决更多的类似问题。

如在教学苏教版《数学》一年级下册“两位数加整十数、一位数（不进位）”时，教材提出的问题是：大客车和中巴车一共有多少座？如果把它抽象为数学问题，即为求45与30的和是多少，因此列式为45+30。接着，教材引导学生用数学的思想和方法来解决这一问题。为了便于学生直观地、形象地理解算理和算法，教材采用操作小棒、拨计数器或画示意图等方法进行探究。在操作小棒、拔计数器的基础上，教材给出抽象的算法：45+30，先算40+30=70，再算70+5=75。最后，把75个一还原成75座，从而解决了课始提出的问题。同样，教材在教学45+3时，几乎采用了同样的编排过程。为了强化学生对算理和算法的理解，教材还进行了对比，问：45+30与45+3有什么不同？让学生在对比中进一步理解具体算理，建构具体算法，并逐步向一般化的算法进发。

此外，教材在练习中也注重渗透建模思想，注重让学生感悟建模过程和方法。它紧紧围绕教学的重点、难点和关键，从具体的算理和算法出发，逐步向一般化的、抽象的算理和算法进发，直到学生建构一般化的算理和算法。在此基础上引导学生运用模型，形成运算技能，并运用到解决现实问题中去。

正因如此，教师在钻研教材时，应深刻领会编者意图，并切实遵循建模过程进行设计，从而引领学生逐步经历这一数学化的过程，发挥过程的育人价值。

二、新授时做实建模过程

领悟到教材的建模思想后，具体教学时就应该按建模的过程施教，要引导学生逐步从具体形象思维过渡到表象思维，再过渡到抽象思维，从而不断提升建模的层次和水平。教材往往从具体的、特殊的例子出发，引导学生解决具体的一道算式的计算问题，从中探明算理和算法，但教师要适时引导学生从一例、几题到一类，从特殊到一般，從具体到抽象，逐步建构更具概括性的一般的算法模型。可采取集中观察和比较，逐步分析和归纳，不断抽象和概括的策略，从而让蕴含在各种具体算式中的一般算法逐步显现出来，并引导学生及时提炼。

如在教学上述“两位数加整十数、一位数”时，在比完45+30与45+3的不同算法后，一位教师充分利用书后的习题，引导学生逐步建构一般化的算法模型。他先让学生在计数器上画一画计算23+20的过程，填出结果，并让学生在头脑中回忆刚才的拨珠过程，探寻计算方法。接着，让学生想象23还可能加几十，应该怎样拨珠，得数是多少。最后，引导学生集中观察这些等式，思考：都是23加几十，都是怎样算的？学生发现：都是把23十位上的“2”与几十的“几”相加，也就是把十位上的数与十位上的数直接相加。在此基础上，教师引导学生建构出两位数加整十数的一般化的算法模型。同样，在计算23加一位数时，也是这样设计的。这样设计不但便于学生体悟算法模型建构的一般过程和方法，实现对具体情境和算式的适时超越，而且便于学生发现算式之间的内在联系，学会在变中找不变，感受函数思想，还便于其学会分析、比较、归纳、抽象和概括，从而学会数学建模。

笔者认为，在学生得出一般的算法后，教师不要急于让学生运用算法进行计算，而要引导学生及时回顾和反思建模过程，如我们是如何逐步探究的？先干什么？再干什么？最后干什么？采用了哪些方法？……从而帮助学生体会建模过程和方法，积累建模经验，感悟建模思想。

三、沟通时感悟建模方法

《义务教育数学课程标准（2011年版）》指出，数学知识的教学，要注重知识的“生长点”和“延伸点”，把每堂课教学的知识置于整体知识体系中，注重知识的结构和体系，处理好局部知识和整体知识的关系，引导学生感受数学的整体性……为此，在具体建构了一类算式的算法模型后，教师还要注重沟通相关算法之间的内在联系，把新知识纳入学生原有的知识体系中，从而整体地建构一类算式的算法体系，并让学生感悟建模方法、积累建模经验。

如在教学苏教版《数学》四年级下册“三位数乘两位数”例1后，教师有必要对相关算式的算法进行系统梳理，因为这是整数乘法最后一部分内容。教师需要引导学生串点成线、连线成片、结片成网，形成整体的算法体系。一位教师是这样设计的：他从本课所学的三位数乘两位数开始，引导学生回顾和反思三位数乘两位数的算法，再由乘数是两位数，想到曾经学过的两位数乘两位数是怎么计算的。照这样推想，以后还会学习几位数乘两位数？学生说：四位数乘两位数、五位数乘两位数……这些新的乘法你会算吗？学生认为简单，与之前的一样，仍然是先分后合，即先用两位数个位上的数去乘多位数，得到多少个一，积的末尾与个位对齐，再用两位数十位上的数去乘多位数，得到多少个十，积的末尾与十位对齐，最后把两层积相加。学生建构了乘数是两位数的算法模型后，教师又由三位数乘两位数开始，引导学生类推出因数是三位数的算法模型。

四、运用时增强建模意识

在建立算法模型后，要引导学生直接运用模型解决相关的问题，使其在应用中进一步体会模型的好处和价值，从而亲近模型、喜爱模型、自觉运用模型。此外，为了让学生在应用中有新发现、新感悟和新提升，教师仍要引导学生主动思考，不断探索和发现，适当尝试建立新的模型，如发现新的运算规律和运算性质等，以增强学生的建模意识。

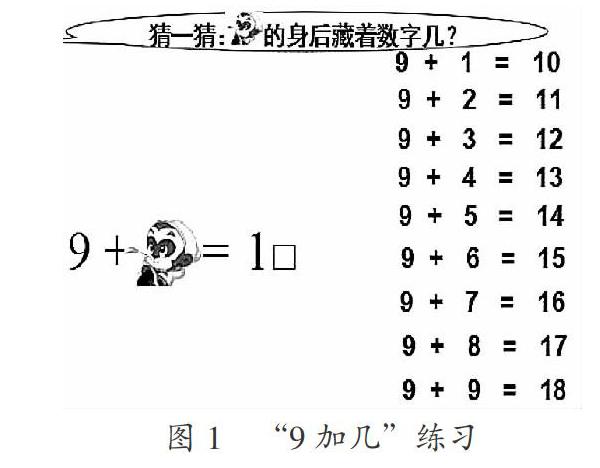
如在教学苏教版《数学》一年级上册“9加几”的练习环节，为了促使学生有新的发现和提升，教师让学生根据算式，思考孙悟空的身后藏着数字几（图1）。

在学生有序地一一算出9道算式的得数后，教师引导学生从中找规律，集中观察所加的数与得数的个位上的数之间的关系。学生发现：9加几的得数个位上的数都比所加的那个数少1，十位上多了一个1。教师追问：那个少了的1到哪里去了？学生说：移到9那边与9凑成1个十了，所以十位上多了1，也就是1个十。教师继续追问：在这些算式中，你认为哪道算式最重要？为什么？学生认为9+1=10最重要，因为其他算式都是根据它推算出来的。接着，教师单独出示9+5=1□、9+□=17，问：现在你能运用规律直接说出方框里的数吗？是怎么想的？学生迅速说出分别是“4”“8”，并说出理由。学生找到新规律后，算得更快了，还可以逆向计算。他们更乐意找规律，更乐意数学建模了。

其实，在教学小数和分数的四则运算时，也可以这样渗透，但要做到：有意、有序和有度，不任意拔高，不急于求成，不统一要求。只要我们坚持不懈，久久为攻，就一定有效。当然，上述四个方面不是相互独立和截然分开的，而是密切联系、相互交融的有机整体，在教学的不同阶段既要相互兼顾，又要各有侧重。

[责任编辑：陈国庆]