直流分布式电源系统稳定性判据研究综述

王久和，王勉，吴学智，李建国，唐芬，张雅静

直流分布式电源系统稳定性判据研究综述

王久和1，王勉2，吴学智2，李建国1，唐芬2，张雅静1

（1．北京信息科技大学，北京市 海淀区 100192；2．北京交通大学，北京市 海淀区 100044）

在实际工程应用中，需要利用稳定性判据判断直流分布式电源系统(direct current distributed power system，DCDPS)的稳定性，以便采取合适的控制策略。因此，DCDPS稳定性判据成为国内外学者研究的热点。对基于等效源变换器(子系统)和负载变换器(子系统)的稳定性判据、基于母线电压控制变换器和母线电流控制变换器的稳定性判据、基于无源性的稳定性判据、大扰动信号情况下稳定性判据的基本思想、特点进行分析。指出这些稳定性判据的优点与不足，给出了DCDPS稳定性判据研究的趋势，提出了基于无源性的稳定性判据和其他判据相结合的稳定性判断新方法。

直流分布式电源系统(DCDPS)；稳定性判据；源变换器；负载变换器；次回路增益；无源性；大扰动

0 引言

在工业中，由电力电子变换器(power electronic converter，PEC)，如整流器或DC/DC变换器，将交流电能或直流电能传送到直流母线上；直流母线通过PEC(如DC/AC逆变器或DC/DC变换器)将电能传送给各类负载，具有这种功能的多PEC系统称为直流分布式电源系统(DC distributed power system，DCDPS)。由于PEC具有重量轻、尺寸小、能量转换高效、电源并联易实现及直流型可再生能源易结合等优点，DCDPS具有适应性强、可靠性高、预期寿命长、重量轻、尺寸小和成本低等优点，在电动汽车[1-4]、舰船[5-6]、航天器[7-8]、通信基站以及大型计算机供电系统中得到了广泛应用。尽管每个PEC是稳定的，但在DCDPS中PEC的相互作用等因素的影响，导致DCDPS稳定性下降甚至不稳定，成为DCDPS进一步推广应用的瓶颈。因此，利用稳定性判据判断DCDPS稳定性是国内外学者研究的热点。对此，本文对国内外基于等效源变换器(source converter，SC)和负载变换器(load converter，LC)的DCDPS稳定性判据、基于母线电压控制变换器(bus voltage-controlled converter，BVCC)和母线电流控制变换器(bus current- controlled converter，BCCC)的DCDPS稳定性判据、基于无源性的稳定判据(passivity-based stability criterion，PBSC)及在大扰动信号下的稳定性判据进行论述与分析，指出这些判据的优点与不足，提出了可行的研究方向。

1 DCDPS稳定性判据国内外研究现状

1.1 影响DCDPS稳定性的因素

影响DCDPS稳定性的主要因素如下：1）DCDPS中各子系统或PEC之间的相互作用；2）PEC带恒功率负载(constant power load，CPL)或PEC在负反馈控制时，在控制环路带宽内PEC输入侧呈CPL特征，具有负阻特性；3）DCDPS的执行装置及传感器、计算、PWM信号及锁相环的延时；4）电压源变换器在某些频率范围内具有负阻特性[9]；5）基于小信号模型控制器在大扰动信号下控制性能下降。

1.2 DCDPS稳定性判据

1.2.1 基于等效SC和LC的稳定性判据

为研究DCDPS的稳定性，通常将DCDPS等效为SC和LC相互作用的级联结构，如图1所示。假定等效SC和LC是稳定的，且具有良好的动态性能。

图1 DCDPS的SC与LC等效

由图1可得，DCDPS输入到输出的传递函数为

由于假定s和l是稳定的，mgl就决定了DCDPS的稳定性，当mgl的Nyquist曲线不包括点(−1,0)时，DCDPS是稳定的。文献[10-21]论述了基于mgl的Nyquist曲线DCDPS稳定性判据，如Middlebrook、GMPM(gain margin and phase margin)、OA(opposing argument)、MP(maximum peak)、ESAC(energy source analysis consortium)、RES(root exponential stability)、T-SI(three-step impedance)等稳定性判据。

1）Middlebrook稳定性判据。

由式(2)可知，如果mgl的Nyquist曲线在单位圆内，就不会环绕点(−1,0)，DCDPS就是稳定的。以平面原点为圆心的单位圆外区域为mgl禁止区域(简称“禁区”)，如图2所示。

图2 Middlebrook稳定性判据禁区

2）GMPM稳定性判据。

由于Middlebrook稳定性判据对阻抗比的要求过于严格，在实际系统中难以满足。为此，1995年Wildrick提出了基于禁区概念的阻抗判据，基于禁区的GMPM稳定性判据[9-10]是指在复平面中设定一个禁区：

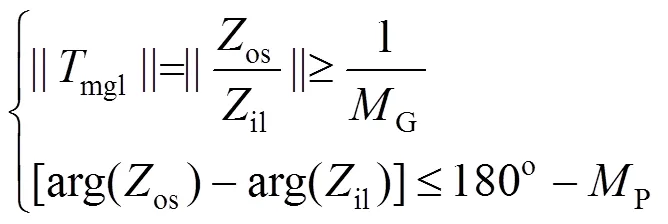
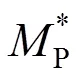
图3 GMPM稳定性判据禁区

3）OA稳定性判据。

在GMPM稳定性判据基础上，Feng等[12]提出了OA稳定性判据，如图4所示。对于1个源子系统给个负载子系统供电的DCDPS(见图5)，il=il1//···//iln，次环路增益为

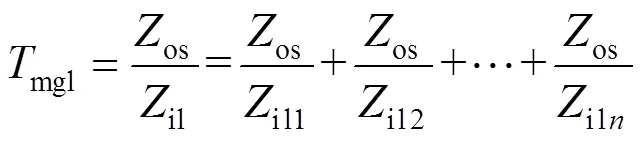
该OA稳定性判据禁区为

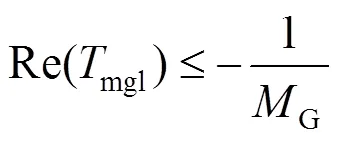
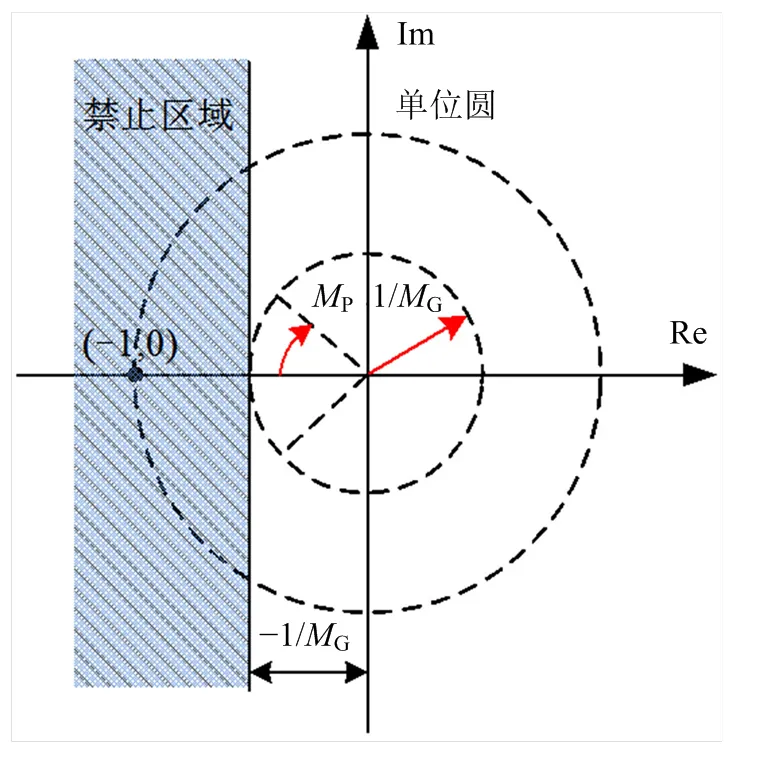
图4 OA稳定性判据禁区

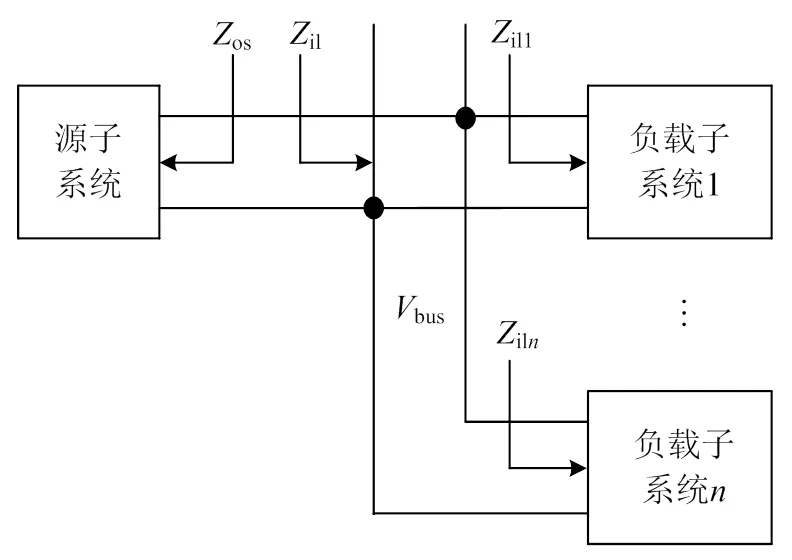
图5 1个源子系统给n个负载子系统供电的DCDPS

若源子系统的功率为os，负载子系统的功率为il1,il2,···,iln，并满足

则每个负载子系统次环路增益os/ilk(=1,2,···,)禁区为

若次环路增益的Nyquist曲线不进入式(5)或式(7)确定的禁区，则DCDPS就是稳定的。

4）MP稳定性判据。

幅值裕度和相位裕度在一定程度上能保证DCDPS的相对稳定性，但当mgl的Nyquist曲线靠近点(−1,0)时，系统的相对稳定性下降，则使用幅值裕度和相位裕度不能保证系统有良好的相对稳定性。对此，MP稳定性判据[13-15]限定了mgl的Nyquist曲线到点(−1,0)的距离，可保证系统具有一定的稳定裕度。以点(−1,0)为圆心、0为半径的圆禁区可保证系统的稳定裕度，该禁区如图6所示，可表示为

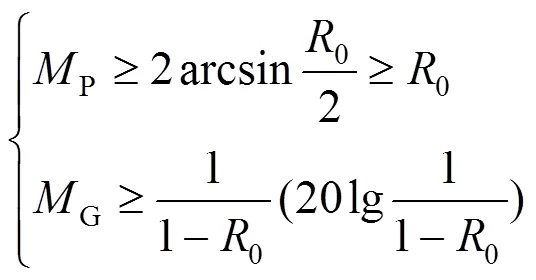
MP稳定性判据可采用直流母线上加入小信号电压扰动的方法在线监控DCDPS的稳定裕度。MP稳定性判据主要用于系统参数发生微小变化时的DCDPS稳定性判断。

5）ESAC稳定性判据。

ESAC稳定性判据[10,16-17]禁区由始于无穷远、平行于实轴、终于单位圆的2条直线，以及始于单位圆、终于的2条直线组成，如图7所示。ESAC禁区一般设置满足系统稳定运行的相位裕度和幅值裕度分别为60°和6dB。ESAC稳定性判据适用于在给定源阻抗情况下的负载阻抗设计。稳定性可由以频率、相位及幅值作为3个轴的三维导纳空间描述[18]。ESAC稳定性判据可根据DCDPS的稳定运行要求设置合适的相位裕度和幅值裕度。ESAC稳定性判据给出的禁区面积随相位裕度和幅值裕度的不同而发生变化。在相位裕度和幅值裕度相同的情况下，ESAC稳定性判据禁区面积相对于其他判据更小，其保守性相对较小。

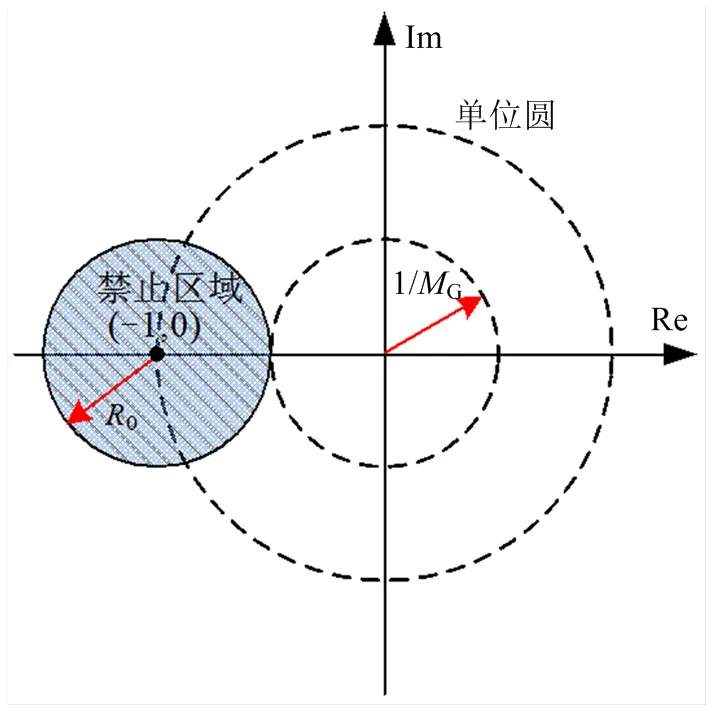
图6 MP稳定性判据禁区

图7 ESAC稳定性判据禁区

6）RES稳定性判据。

RES稳定性判据[10,19]禁区如图8所示，与ESAC类似，二者对设计影响差别较小，RES稳定性判据禁区用连续函数表示。然而，与ESAC相比，RES在基于源阻抗(负载导纳)计算负载导

图8 RES稳定性判据禁区

纳(源阻抗)约束方面具有优越性。

RES稳定性判据可通过引入函数()定义：

式中：³2，且为偶整数；Re(s)和Im(s)分别为复变量的实部和虚部；、及为正实常数。

RES稳定性判据禁区由满足平面点集 定义：

则要求

RES稳定性判据的附加性能可表示为

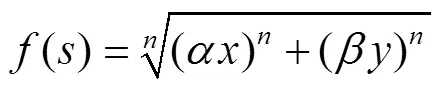
由式(12)可知，在-平面，RES是一超椭圆。另外，当保证>0时，在平面RES稳定性判据禁区不是封闭的。在Re()→−∞，→0时，RES判据禁区变成水平线，即

除上述稳定性判据外，文献[20]基于以上等效结构，利用阻抗方法研究局部稳定性，利用状态空间模型特征值分析方法研究大范围稳定性；文献[21]提出了电力电子系统阻抗和的稳定性判据；文献[22]利用双端口小信号模型获得了稳定性判据。

7）T-SI稳定性判据。

T-SI稳定性判据[10,22-23]是研究一个源子系统连接到个并联负载子系统的DCDPS(如图5所示)的小信号稳定性问题。假设所有调节的子系统均是PWM控制的DC/DC变换器，第个负载子系统的负载阻抗表示为lk。

定义第个负载子系统的映射纯阻抗lk为

T-SI稳定性判据突破了前述判据的保守性，因为它不假设式(1)中s必须是稳定的传递函数。事实上，在一个不稳定的独立源子系统的情况下，如果采用式(1)次环路增益，会产生不正确的稳定性判断。因此，阻抗判据不适用于(1)中定义的次环路增益，而是采用扩展的次环路增益：

式中：os()为源子系统的输出阻抗；il()为所有个负载子系统并联的等效输入阻抗。

T-SI稳定性判据包括以下3个步骤：1）利用负载子系统与相应的映射纯阻抗初步分析系统的稳定性；2）进行阻抗测量，先测量连接映射纯阻抗的源子系统输出阻抗，再测量每个负载子系统的输入阻抗；3）对于图3所示DCDPS，利用emgl的Nyquist曲线判断系统稳定性。

1.2.2 基于BVCC和BCCC的稳定性判据

1）BVCC和BCCC。

基于等效SC和LC的稳定性判据都是针对由源变换器(子系统)和负载变换器(子系统)组成的级联系统(见图1)提出的。在实际工程应用中，除级联结构外，DCDPS还有其他结构形式，如带储能单元的DCDPS[24]。具有发电、储能单元的DCDPS如图9所示。

图9 带发电及储能单元的DCDPS

当PV阵列不足以提供负载所需的能量时，双向变换器将电池的能量补充给负载变换器，此时它表现为一个源变换器；而当PV阵列提供的能量大于负载所需能量时，则多余的能量通过双向变换器存储到电池中，此时双向变换器表现为一个负载变换器。因此，如果用1.2.1所述的阻抗判据判断该系统的稳定性，则需要考虑PV阵列不足以提供负载所需的能量和PV阵列大于负载所需能量这2种系统工作模式，这使系统稳定性问题的分析难度变大。

为了解决上述问题，不再以SC或LC来区分 DCDPS中的变换器，而将其归类为BVCC和BCCC。BVCC指直接或间接控制其在系统直流母线侧端口电压bus的变换器，如图10(a)所示；BCCC指直接或间接控制其在系统直流母线侧端口电流bus的变换器，如图10(b)所示。

2）DCDPS通用阻抗稳定性判据。

根据DCDPS中的变换器是控制母线侧的端口电压或端口电流，将其划分为BVCC和BCCC，于是可得DCDPS的统一形式如图11所示。图11中(≥1)个BVCC并联在直流母线上，控制各自母线侧的端口电压；(≥1)个BCCC并联在直流母线上，控制各自母线侧的端口电流；busvj(= 1,2,···,)和busck(=1,2,···,)分别是第个BVCC和第个BCCC母线侧的端口电流。

利用DCDPS二端口小信号模型确定busvj和busck，根据图11可得DCDPS级联环路等效增 益为

图10 BVCC和BCCC

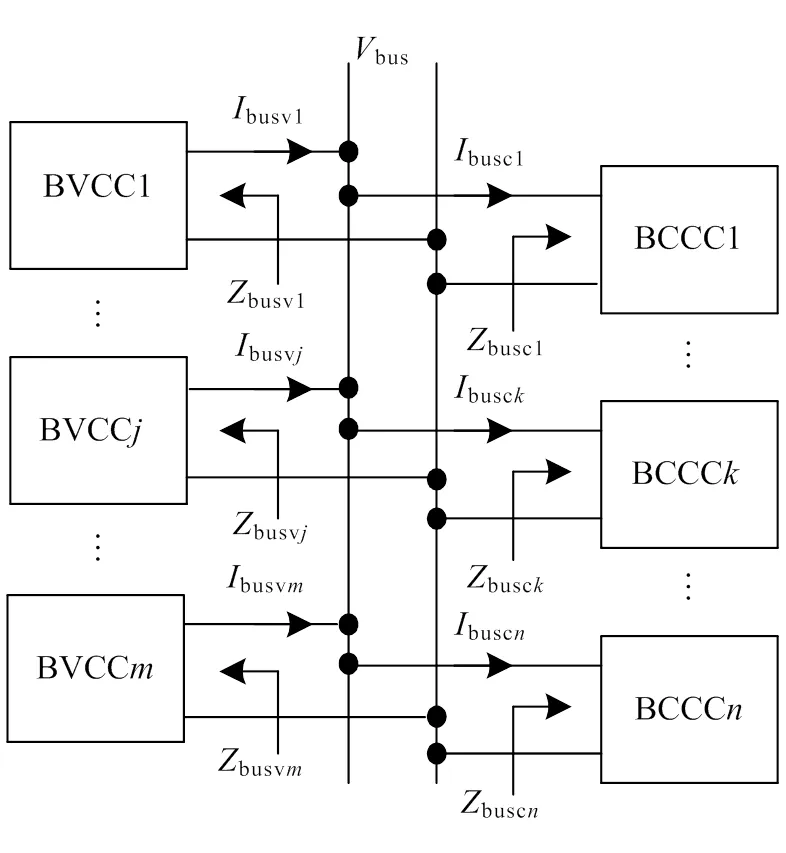
图11 DCDPS的统一形式

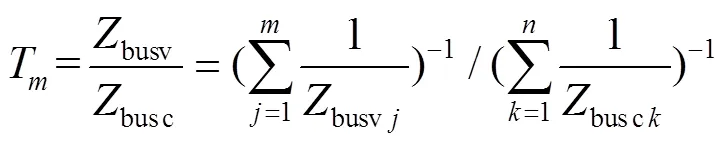
式中：busv和busc分别为BVCC和BCCC母线侧的端口阻抗。

根据式(17)可得DCDPS通用阻抗稳定性判据[25-27]为：①每个变换器单独工作是稳定的；②m满足Nyquist判据的稳定条件。

根据通用阻抗判据来判断DCDPS稳定性步骤为：①将DCDPS转化为DCDPS的统一形式，确定系统中的BVCC和BCCC及其数量和；②将BVCC和BCCC在母线侧的端口阻抗、和的值代入式(17)，根据m是否满足Nyquist判据来判断系统的稳定性。

1.2.3 PBSC稳定性判据

1）无源性与稳定性。

端口网络(系统)如图12所示，网络(系统)无源性的充要条件为：外部送给端口网络(系统)的能量()为非负的[28-29]，即

基于Parseval定理中信号在时间域内的总能量与频域内的总能量相等的原理，可将能量从时域转化为频率表示，即

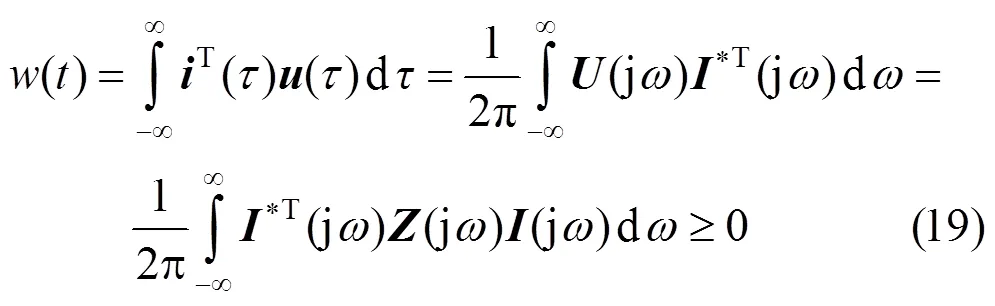
式中：(j)和(j)分别为()和()的傅里叶变换；(j)=(j)(j)；*表示共轭复数。

若网络(系统)是无源的，则网络(系统)是稳定的。由式(19)可以看出，若(j)的实部为正，则()＞0，网络(系统)就是无源的，即网络(系统)是稳定的。

2）DCDPS的等效。

PBSC是基于母线总阻抗的无源性而不是小回路增益的Nyquist判据。为利用阻抗判断DCDPS的无源性，需对其进行等效。考察图13(a)所示连接到由个源变换器和个负载变换器组成的单母线DCDPS，对于给定的系统，可简化为源子系统和负载子系统相互作用的网络，如图13(b)所示；再等效成单端口网络，如图13(c)所示。在图13(b)中，源子系统阻抗os=1//···//Z，负载子系统阻抗il=Z+l//···//Z+m；图13(c)中bus为

bus=os//il=1//···//Z//Z+1//···//Z+m(20)

图13 DCDPS及其等效网络

3）DCDPS的PBSC。

从直流母线端来看，图13(c)的1-端口网路的阻抗为bus，理论上应按式(20)进行计算，则需计算或测得Z(=1,2,···,+)，这样需大量计算或测量，导致确定bus难度大。对此，通过外部信号源给母线注入电流inj()(见图13(b))，并实施测量；于是可得

bus()=bus()/inj() (21)

式中inj()为外部装置(信号源)注入的电流。

bus()是所有变换器输入/输出阻抗的并联组合，如果bus()没有右半平面(right half plane，RHP)极点，且Re[bus(j)]≥0，则DCDPS是无源的[30-31]，即DCDPS是稳定的。Re[bus(j)]≥0等效于−90°≤arg[bus(j)]≤90°，相应的阻抗对所有频率具有正实部，这也意味着bus(j)的Nyquist曲线必须位于RHP。bus(j)的相位是bus(j)和inj(j)的相位差。如果bus(j)的相位在−90°和90°之间，对所有频率进入端口的平均功率是正的，则系统消耗能量，即系统是无源系统。如果bus(j)的相位等于90°或−90°，平均功率是0，则系统是无损的。如果bus(j)的相位小于−90°或大于90°，平均功率是负的，则系统可能产生能量，即系统是有源系统。

关于PBSC在DCDPS中的应用、阻抗测量及相应的控制器设计详见文献[32-35]。

1.2.4 大扰动信号情况下稳定性判据

为克服小信号模型在大扰动信号情况下的DCDPS稳定性判断问题，近几年国内外学者进行了相关研究。基于Lyapunov稳定理论，文献[36]研究了直流微电网大信号稳定性的参数边界条件，通过分析电流小扰动对母线电压的影响，提出了并联阻抗稳定性判定方法；文献[37]估计了系统的渐进稳定域，进行了大扰动信号稳定性研究。基于混合势函数理论，文献[38]提出了适用于直流微电网的稳定性判据，该判据表明下垂控制的直流微电网的大扰动信号稳定性与各变流器系统参数、各电源输出功率占负载功率比例的相关性；文献[39]用混合势函数理论和Lyapunov特征值法对直流微电网的功率界限进行了估计，同时利用T-S模糊模型方法和逆轨迹法对直流微电网的渐进稳定域进行了估计；文献[40]建立了基于混合势函数Brayton-Moser的模型，得到大扰动信号情况下的稳定性判据。

2 DCDPS稳定性判据分析

2.1 基于SC和LC的稳定性判据分析

根据1.2.1对稳定性判据的论述可知，基于次环路增益的DCDPS稳定性判据总体上有以下共同点：1）利用了基于源阻抗/负载阻抗比(次环路增益)的稳定条件；2）基于次环路增益极坐标图的禁区；3）在给定源阻抗情况下的负载阻抗设计。

通过对基于等效SC和LC的DCDPS稳定性判据的分析，其不足如下：

1）所有这些稳定性判据只提供DCDPS稳定性的充分条件，不是充要条件；对具有最小保守性的ESAC判据，在违背充分条件情况下DCDPS仍可以稳定。

2）所有这些稳定性判据是通过定义一个源子系统和一个负载子系统，即在假定给定的功率流向情况下使用稳定性判据；在DCDPS运行时SC和LC角色变换(功率流动方向改变)导致稳定性判据使用难度大。

3）所有这些稳定性判据主要实际困难是先分别测量源子系统输出阻抗和负载子系统输入阻抗，再进行后期处理，计算次环路增益。由于计算复杂，不适用于在线稳定性监测。

4）除Middlebrook稳定性判据之外，其他判据不利于设计的公式化。

Middlebrook稳定性判据的优点为：1）仅基于阻抗幅值进行设计，从而简化了应用；2）通过应用Extra Element Theorem[41]解决了DCDPS动态性能的相互影响问题。它的主要不足为：1）可能导致DCDPS设计的人工保守性(导致滤波元件远大于所需要的)；2）如果源阻抗和负载阻抗相交换，就违背了Middlebrook稳定性判据，这是因为如果os/il位于单位圆内，则il/os一定位于单位圆外。

对于GMPM稳定性判据，由于它定义了一个小的禁区，相对于Middlebrook判据具有更小的保守性，同时可保证所需的DCDPS增益和相位。OA稳定性判据可认为是GMPM的一个改进，其优点为：1）适用于多负载子系统的DCDPS；2）提出了实际测量次环路增益稳定裕度的方法。其缺点为：当和其他弱保守性判据一起使用时，OA稳定性判据就会失效。

MP稳定性判据可保证系统具有一定的稳定裕度，但并不能保证系统的稳定性，必须使用Nyquist判据进行辅助判定。其不足为：1）不适用于阻抗设计，亦很难在波特图上对判据进行计算；2）禁区并不能保证阻抗比os/il的Nyquist曲线不包围点(−1,0)，因此，当DCDPS工作点发生变化时，基于该禁区的监控方法不能用于判断系统的稳定性。

ESAC稳定性判据及其改进稳定性判据RES判据在保证所需的增益和相位裕度情况下，进一步减小了阻抗比判据的保守性，并对组件分组不敏感。但RES稳定性判据有利于设计公式化。RES与MP稳定性判据有共同的缺点，即不适用于阻抗设计。

T-SI稳定性判据是两级DCDPS有效的小信号稳定性分析方法，它不依赖于复杂的数学模型，特别是有关子系统的信息，而注重子系统输入/输出阻抗的测量。基于次环路增益的T-SI稳定性判据，借助于必要的转换可扩展到多级DCDPS或其他分布式系统。由于小信号平均建模和连续导通模式是它的理论基础，T-SI稳定性判据对大扰动信号稳定性分析和快时标不稳定预测是无效的。综合来看，可认为T-SI稳定性判据比其他稳定性判据应用更普遍。

2.2 基于BVCC和BCCC的稳定性判据分析

利用BVCC和BCCC将DCDPS转化为DCDPS的统一形式，则基于BVCC和BCCC的DCDPS稳定性判据突破了以上稳定性判据的限制。与T-SI稳定性判据相同，基于BVCC和BCCC的稳定性判据也是基于小信号模型，需计算各变换器的输出阻抗或输入阻抗，具有复杂性；同时也不适用于大扰动信号情况下的稳定性分析。

2.3 PBSC的稳定性判据分析

PBSC是一种基于不同概念的稳定性判据。该方法是利用整体母线阻抗的无源条件，而不是利用给定系统接口的阻抗比条件，且PBSC不需要假设子系统的稳定性。

PBSC的优点为：1）PBSC可很容易地处理多个相连变换器的DCDPS；2）由于没有功率流向假设，在功率流向变化时PBSC也适用；3）与其他稳定性判据不同，PBSC对元件分组并不敏感，因此它可减少人工设计的保守性；4）不需要次环路增益的在线测量，母线阻抗在线测量容易实现，不需要复杂的后期处理，适用于系统稳定性的监测；5）PBSC适用于设计稳定控制器，对于DCDPS通过控制器可引入有源阻尼阻抗；6）PBSC消除了前面所有判据阻止围绕点(1,0)的假设条件。

PBSC的主要不足为：1）PBSC仅仅提供了一个稳定的充分条件，而非必要条件，即如果系统总线阻抗的Nyquist图完全位于右半平面，则由源子系统与负载子系统互联形成的系统是无源的，且一定是稳定的，然而，如果对于某些频率，系统母线阻抗的Nyquist图位于左半平面，则形成的系统是有源的，就不能判断系统的稳定性；2）PBSC是基于对整个系统母线阻抗的无源评价，很难定义稳定裕度，而基于次环路增益的判据可定义稳定裕度。

2.4 大扰动信号情况下的稳定性判据分析

大扰动信号情况下的稳定性判据是基于大信号模型或非线性模型，以及Lyapunov稳定理论和混合势函数理论进行稳定性研究的，可保证大扰动信号和复杂的非线性因素影响情况下系统的稳定性；同时，也适用于小信号情况下的稳定性研究。因此，该基于能量或功率的稳定性判据更适用于工程实际。由于基于混合势函数的稳定性判据具有功率属性，因此可使系统具有良好的动态响应。其不足为模型建立、稳定域与系统参数的关系比较复杂，相对于小信号模型控制器设计难度更大。

3 DCDPS稳定性判据研究趋势

对DCDPS稳定性判据进行综合分析可知，Middlebrook、GMPM、OA、MP、ESAC及RES稳定性判据都具有一定的保守性，会导致系统在设计之初就付出了一些不必要的代价，包括系统性能下降、滤波器尺寸增大、母线电容增大等。T-SI稳定性判据和基于BVCC和BCCC的稳定性通用判据虽能克服上述判据的不足，但都是基于小信号模型，需要复杂的计算，不适用于大扰动信号及非线性情况下DCDPS稳定性的判断。PBSC可克服1.2.1和1.2.2节中稳定性判据的不足，但只是稳定的充分条件，而非必要条件；大扰动信号情况下DCDPS稳定性判据适用于大扰动信号及非线性情况下DCDPS稳定性的判断，值得进一步研究。

因此，对DCDPS稳定性判据可进行以下4个方面的研究：

1）PBSC与Nyquist判据融合研究。由于Nyquist判据提供了充要条件，并对稳定裕度有良好的刻画，PBSC通过母线阻抗的无源性给出了稳定的充分条件，因此，在系统稳定的前提下，研究PBSC与Nyquist判据的内在联系，结合其优点，对PBSC予以改进，使其成为DCDPS稳定的充要条件，并可对稳定裕度进行量化。

2）多母线DCDPS稳定性判据研究。由于多母线DCDPS在电动和混合电动车辆、电动飞机电力系统等获得了应用，本文论述的判据已不适用。基于由多个无源子系统组成的系统应是无源系统的思想[26]，研究多母线DCDPS稳定性判据。

3）阻抗测量研究。无论哪种稳定性判据，都需要进行阻抗测量。因此，需研发高性能宽带阻抗识别系统，测得精确的DCDPS母线阻抗、子系统的输出阻抗或输入阻抗，对系统稳定性进行准确判断。

4）基于混合势函数理论的无源稳定性研究。鉴于大扰动信号、负阻特性等非线性因素对稳定性的影响，可基于混合势函数建立Brayton-Moser模型，研究系统稳定性问题；同时，基于功率成形设计无源控制器，保证系统的稳定性，提高系统的动态性能。

4 结论

对国内外基于等效SC和LC的稳定性判据、基于BVCC和BCCC的稳定性判据、PBSC稳定性判据及大扰动信号情况下稳定性判据进行了系统论述，分析了各种稳定性判据的优点与不足。基于PBSC的优势，提出了以PBSC为主，融合Nyquist、混合势函数理论，研究适用于单母线和多母线DCDPS稳定性判断的新方法。

[1] Tabari M，Yazdani A．A mathematical model for stability analysis of a DC distribution system for power system integration of plug-in electric vehicles[J]．IEEE Transactions on Vehicular Technology，2015，64(5)：1729-1738．

[2] 梁珺，冯洪涛，唐巍，等．消纳分布式电源和电动汽车的交直流混合中压配电网供电模式[J]．分布式能源，2018，3(1)：39-49．

[3] 夏晨阳，赵书泽，杨颖，等．电动汽车无线充电系统研究综述[J]．广东电力，2018，31(11)：3-14．

[4] 岳红权，王建渊，杨文宇，等．基于互联网+的充电站配电设备在线监测研究[J]．电网与清洁能源，2018，34(4)：29-35.

[5] 康少波．船舶电力变换系统的稳定性分析与控制研究[D]．哈尔滨：哈尔滨工程大学，2013．

[6] Siegers J，Santi E．Stability analysis and control design for an all-electric ship MVDC power distribution system using a passivity based stability criterion and power hardware-in-the-loop simulation[C]//IEEE Electric Ship Technologies Symposium (ESTS)．VA，USA：IEEE，2015：86-92．

[7] 万成安，于磊，刘建强．航天器直流电源系统稳定性分析方法研究[J]．航天器工程，2009，18(2)：14-19．

[8] Iftikhar M U，Baig M S．Stability study of spacecraft electrical power system with constant power loads [C]//IEEE 14th International Multitopic Conference (INMIC)．Karachi，Pakistan：IEEE，2011：217-221．

[9] Harnefors L，Wang X F，Yepes A G，et al．Passivity-based stability assessment of grid- connected VSCs：an overview[J]．IEEE Journal of Emerging and Selected Topics in Power Electronics，2016，4(1)：116-125．

[10] Riccobono A，Santi E．Comprehensive review of stability criteria for DC power distribution systems [J]．IEEE Transactions on Industry Applications，2014，50(5)：3525-3535．

[11] Wildrick C M，Lee F C，Cho B H，et al．A method of defining the load impedance specification for a stable distributed power system[J]．IEEE Transactions on Power Electronics，1995，10(3)：280-285．

[12] Feng X G，Liu J J，Lee F C．Impedance specifications for stable DC distributed power systems[J]．Transactions on Power Electronics，2002，17(2)：157-162．

[13] Vesti S，Suntio T，Oliver J A，et al．Impedance-based stability and transient-performance assessment applying maximum peak criteria[J]．IEEE Transactions on Power Electronics，2013，28(5)：2099-2104．

[14] Vesti S，Oliver J A，Prieto R，et al．Simplified small-signal stability analysis for optimized power system architecture[C]//Twenty-eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC)．Long Beach，USA：IEEE，2013：1702-1708．

[15] 李安寿．分布式电源系统稳定性研究[D]．哈尔滨：哈尔滨工业大学，2014．

[16] Sudhoff S D，Glover S F，Lamm P T，et al．Admittance space stability analysis of power electronic systems [J]．IEEE Transactions on Aerospace and Electronic Systems，2000，36(3)：965-973．

[17] 杨晓平，张浩，马西奎．基于ESAC标准的分布式电源系统稳定裕度监控[J]．电工技术学报，2009，24(8)：14-21．

[18] Sudhoff S D，Glover S F．Three-dimensional stability analysis of DC power electronics based systems [C]//IEEE 31st Power Electronics Specialists Conference．Galway，Ireland：IEEE，2000：101-106．

[19] Sudhoff S D，Crider J M．Advancements in generalized immittance based stability analysis of DC power electronics based distribution systems[C]//IEEE Electric Ship Technologies Symposium．Alexandria，VA：IEEE，2015：207-212．

[20] Simiyu P，Ai X，Bitew G T，et al．Small-signal stability analysis for the multiterminal VSC MVDC distribution network：a review[J]．The Journal of Engineering，2019，16：1068-1075．

[21] Zhong Q C，Zhang X．Impedance-sum stability criterion for power electronic systems with two converters/sources[J]．IEEE Access，2019，7：21254-21265．

[22] Wei Y Q，Luo Q M，Chen S，et al．DC current bus distributed power system and its stability analysis [J]．IET Power Electronics，2019，12(3)：458-464．

[23] Wang X P，Yao R P，Rao F Q．Three-step impedance criterion for small-signal stability analysis in two-stage DC distributed power systems[J]．IEEE Power Electronics Letters，2003，1(3)：83-87．

[24] Indu Rani B，Saravana Ilango G，Nagamani C．Control strategy for power flow management in a PV system supplying DC loads[J]．IEEE Transactions on Industrial Electronics，2013，60(8)：3185-3194．

[25] 张欣．直流分布式电源稳定性研究[D]．南京：南京航天航空大学，2014．

[26] Zhang X，Ruan X B，Tse C K．Impedance based local stability criterion for DC distributed power systems [J]．IEEE Transactions on Circuits and Systems，2015，62(3)：916-925．

[27] 阮新波．直流变换器级联系统：稳定性判据与解决方案[R]．南京：南京航天航空大学，2016．

[28] 王久和．无源控制理论及其应用[M]．北京：电子工业出版社，2010．

[29] Mendez V，Tavakoli M．A passivity criterion for-port multilateral haptic systems[C]//49th IEEE Conference on Decision and Control．Atlanta，GA，USA：IEEE，2011：274-279．

[30] Riccobono A，Santi E．A novel passivity-based stability criterion (PBSC)for switching converter dc distribution systems[C]//Twenty-seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC)．Orlando，FL，USA，2012：2560-2567．

[31] Riccobono A．Stabilizing controller design for a DC power distribution system using a passivity-based stability criterion[D]．South Carolina：University of South Carolina，2013．

[32] Riccobono A，Santi E．Stability analysis of an all-electric ship MVDC power distribution system using a novel passivity-based stability criterion [C]//IEEE Electric Ship Technologies Symposium (ESTS)．Arlington，VA，USA：IEEE，2013：411-419．

[33] Siegers J，Arrua S，Santi E．Stabilizing controller design for multi-bus MVDC distribution systems using a passivity based stability criterion and positive feed-forward control[C]//IEEE Energy Conversion Congress and Exposition (ECCE)．Montreal, QC, Canada：IEEE，2015：5180-5187．

[34] Gu Y J，Li W H，He X N．Passivity-based control of DC microgrid for self-disciplined stabilization[J]．IEEE Transactions on Power Systems，2015，30(5)：2623-2631．

[35] Riccobono A，Siegers J，Santi E．Stabilizing positive feed-forward control design for a DC power distribution system using a passivity-based stability criterion and system bus impedance identification [C]//IEEE Applied Power Electronics Conference and Exposition．Fort Worth，TX，USA：IEEE，2014：1139-1146．

[36] 支娜，张辉，肖曦，等．分布式控制的直流微电网系统级稳定性分析[J]．中国电机工程学报，2016，36(2)：368-378．

[37] Kabalan M，Singh P，Niebur D．Large signal Lyapunov-based stability studies on microgrids：a review[J]．IEEE Transactions on Smart Grid，2017，8(5)：2287-2295．

[38] 厉泽坤，孔力，裴玮，等．基于混合势函数的下垂控制直流微电网大扰动稳定性分析[J]．电网技术，2018，42(11)：5725-5734．

[39] 滕昌鹏，王玉斌，周博恺，等．含恒功率负载的直流微网大信号稳定性分析[J]．电工技术学报，2019，34(5)：973-982．

[40] 刘欣博，高卓．考虑恒功率负载与储能单元动态特性的直流微电网系统大信号稳定性分析[J]．电工技术学报，2019，34(S1)：292-299．

[41] Middlebrook R D，Vorpérian V，Lindal J．The extra element theorem[J]．IEEE Transactions on Circuits and Systems-I：Fundamental Theory and Applications，1998，45(9)：919-935．

Review of Stability Criteria Study for Direct Current Distributed Power System

WANG Jiuhe1, WANG Mian2, WU Xuezhi2, LI Jianguo1, TANG Fen2, ZHANG YA Jing1

(1. Beijing Information Science & Technology University, Haidian District, Beijing 100192, China; 2. Beijing Jiaotong University, Haidian District, Beijing 100044, China)

In practical engineering application, it is necessary to judge the stability of direct current distributed power system (DCDPS) by using stability criteria, so as to adopt appropriate control strategies. Therefore, stability criteria of DCDPS are generally interested by scholars at home and abroad. The basic idea and characteristics of stability criteria based on equivalent source converter (subsystem) and equivalent load converter (subsystem), a bus voltage-controlled converter and a bus current-controlled converter, passivity and large disturbance signal were analyzed. Based on the above analysis, the advantages and defects of the stability criteria were pointed out. The research trends of the stability criteria for DCDPS were put forward, and a new method of stabilitycriteria was proposed by combining passivity-based stability criterion and other stability criteria.

direct current distributed power system (DCDPS); stability criteria; source converter; load converter; minor loop gain; passivity; large disturbance

10.12096/j.2096-4528.pgt.19066

TM712

国家自然科学基金项目(51777012)；北京市自然科学基金‒教委联合资助项目(KZ201911232045)。

Project Supported by National Natural Science Foundation of China (51777012); Beijing Natural Science Foundation-Educational Commission Joint Funding Project (KZ201911232045).

2019-04-27。

(责任编辑 尚彩娟)