基于自抗扰控制的微电网三相不平衡问题研究

钱梦然，李辉，刘新秀

基于自抗扰控制的微电网三相不平衡问题研究

钱梦然，李辉，刘新秀

（上海电力大学自动化工程学院，上海市 杨浦区 200090）

当微电网中三相负载呈现不平衡状态时，会导致三相输出电压不平衡，若采用三相四桥臂逆变器，则可解决此问题。但在0旋转坐标系下，三相四桥臂逆变器输出电压和输出电流会相互耦合。同时若系统中出现负载不平衡工况，直接采用开环控制，因不平衡负载导致输出电压中含有二倍频扰动，所以负载端输出电压仍然处于不平衡状态。针对上述2个问题，建立了三相四桥臂逆变器对应的数学模型，推导被控对象开环传递函数，对三相不平衡问题进行了深入分析。同时根据系统模型信息，设计二阶自抗扰控制器，目的是对轴电压、电流进行解耦，同时可以减少测量原件的个数。并针对由不平衡负载产生的二倍频扰动引入比例谐振控制器，最后通过Matlab/Simulink仿真，验证了该解决方案的有效性。

微电网；三相四桥臂逆变器；不平衡电压；轴解耦；自抗扰控制器(ADRC)；比例谐振控制器

0 引言

当微电网中三相负载呈现不平衡状态时，会导致三相输出电压不平衡，采用三相逆变器可解决此问题。传统逆变器主要有带变压器的三相三桥臂逆变器[1]、分裂电容式三相逆变器[2]和组合式三相逆变器[3]，但以上3种逆变器结构复杂，不利于节约成本。本文选用三相四桥臂逆变器[4]，此逆变器优势在于只需增加一路桥臂，结构简单，同时可以对中性点电压进行控制，因此能够将其运用于带有不平衡负载的场合。但是三相四桥臂逆变器在0旋转坐标系下轴会相互耦合，而且当系统三相负载出现不平衡时，采用开环控制导致系统的三相输出电压也会出现不平衡现象。针对这个问题，通过建立三相四桥臂逆变器对应的数学模型，进行相应数学推导，揭示问题出现的根本原因，同时设计了复合控制器来解决所提到的问题，最后在Matlab/Simulink软件中进行仿真验证。

1 数学模型推导与分析

1.1 dq轴耦合分析

三相四桥臂逆变器拓扑结构如图1所示[5]。其中：dc为直流母线电压；S1—S8为4个桥臂的开关组合；为交流侧滤波电感；n为中性线上滤波电感；为交流侧滤波电容；a，b，c，N对应4个桥臂中点电压；an，bn，cn分别为abc三相负载电压；a，b，c分别为abc三相滤波电感电流；n为中线电感电流；oa，ob，oc分别为abc三相负载电流。

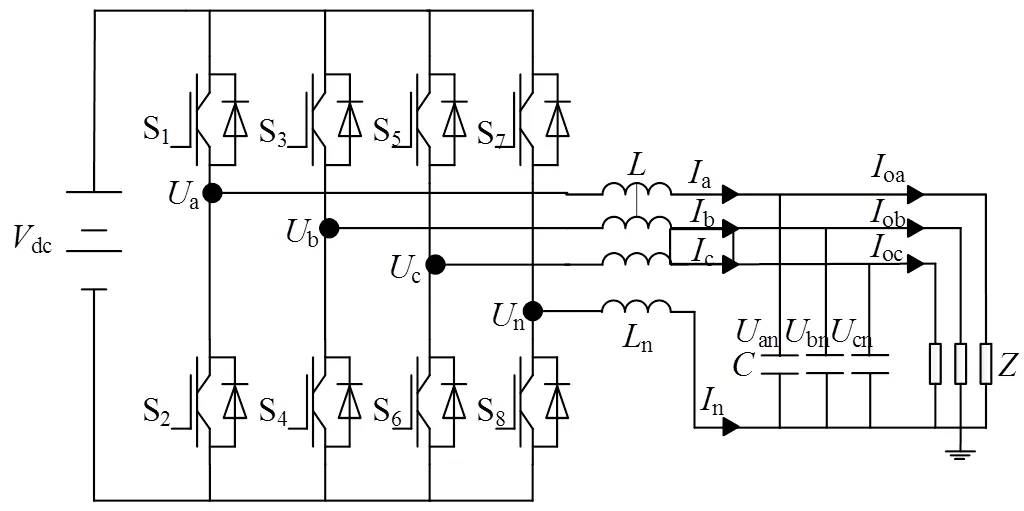
图1 三相四桥臂逆变器拓扑结构

当三相负载处于平衡状态时，忽略开关死区等因素的影响，可以根据图1得到在abc静止坐标系下三相四桥臂逆变器对应的大信号模型[6]，如图2所示。

图2 大信号模型

图2中的受控电压源af、bf和cf关系如 式(1)所示：

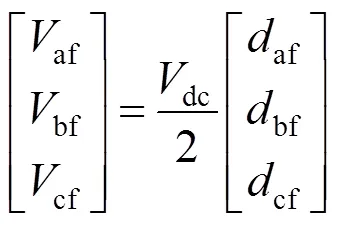
式中：af、bf、cf分别代表abc三相桥臂占空比；af、bf、cf分别代表逆变器abc三相输出电压。

根据图2列写电路方程如下：

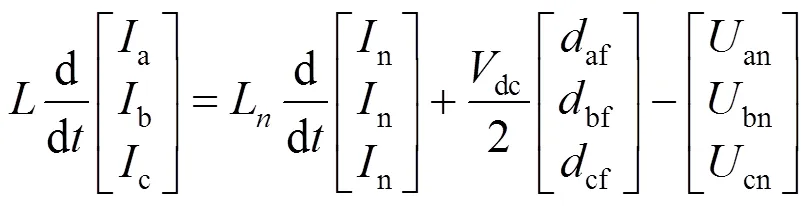
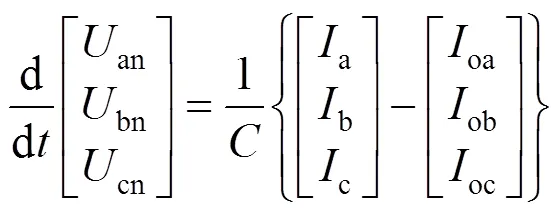
将式(2)与式(3)转换到0坐标系下，则可以得到式(4)和式(5)：

式(4)中为如下矩阵：

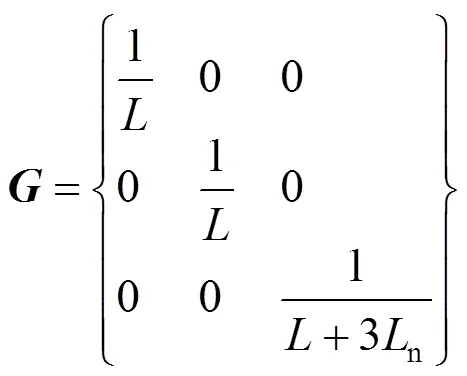
根据式(4)和式(5)得出，在dq0坐标系中，d轴电流与q轴电流呈现相互耦合关系，d轴电压与q轴电压呈现相互耦合关系，而0轴与dq轴没有耦合关系[7]。因此可以由式(4)和式(5)得出dq0旋转坐标系下的平均模型如图3所示。

1.2 三相负载不平衡分析

当三相负载呈现出不平衡状态时，三相输出电压也会呈现出不平衡状态，可采用对称分量法对三相不平衡输出电压进行分析[8-11]，将其分解为正序电压、负序电压和零序电压，如式(6)所示：

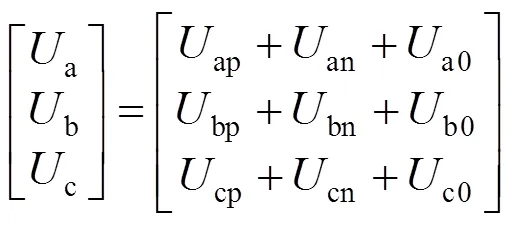
其中：

式(6)中：Up、Un、U0分别为正序、负序、零序分量幅值，=a,b,c；p为正序分量相位；n为负序分量相位；0为零序分量相位。将式(6)转换到0坐标系，如式(7)所示：

由式(7)可知，当负载呈现不平衡状态时，三相输出电压在0旋转坐标系下，正序分量转换为直流量，但负序分量会包含二倍基波频率，零序分量中有基波频率，所以当负载出现不平衡状态时，需要在0旋转坐标系中对交流分量进行相应的抑制。

2 复合控制策略

2.1 复合控制策略的优点

图4为复合控制策略系统图。所提复合控制策略主要有2个优点：1）自抗干扰控制(active disturbance rejection control，ADRC)可将微电网在0旋转坐标系中的耦合项当作总扰动处理，因在ADRC中将电感电流当作扰动项处理，所以不必采集电感电流，可降低成本；2）当微电网负载出现三相不平衡情况，输出电压在0坐标系下会包含二倍频，因此在ADRC基础上引入比例谐振(proportional resonant，PR)控制器，用来消除负载不平衡工况下输出电压中包含的二倍频扰动。

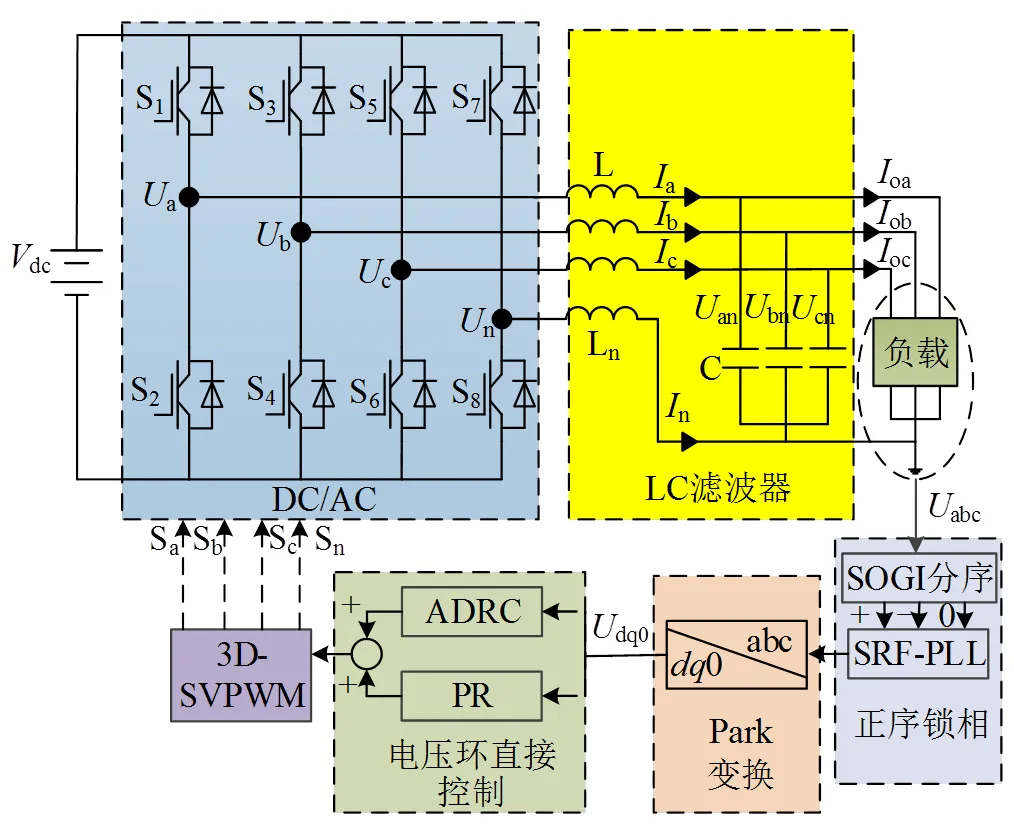
图4 复合控制策略系统图

2.2 ADRC控制器原理设计

2.2.1 ADRC控制器结构

ADRC控制器主要由扩张状态观测器(extended state observer，ESO)和线性状态误差反馈(linear sates error feedback，LSEF)构成[12-13]。其结构如图5所示，其中：1为参考值；2为参考值微分项；1为1与扩张状态观测器中1的差值，1为被控对象输出量的观测值；2为2与扩张状态观测器中2的差值，2为被控对象输出量微分的观测值；3为总扰动观测值；0为线性状态误差反馈输出量；0为调节系数；1为被控对象输入量；为被控对象输出量。

图5 ADRC控制器结构框图

ADRC控制器主要包含2个控制环：1）内环主要作用是负责对总扰动进行观测与补偿，内环是先通过ESO对总扰动进行观测，观测准确之后对扰动进行补偿；2）外环主要功能是通过反馈控制器跟踪给定信号。

2.2.2 ESO结构设计

因被控对象为二阶系统，可将其数学模型转化成式(8)所示积分串联型。

式中：为系统总扰动；为常数。

现将式(8)系统总扰动扩张为第3个状态变量3，则可以将式(8)转换为扩张状态方程：

式中表示总扰动微分项。

根据扩张状态方程式(9)建立扩张状态观测器，如式(10)所示。

式中01、02、03、0、、1与均为可调参数。由式(10)可知，扩张状态观测器阶数为三阶。

其中fal函数表达式为

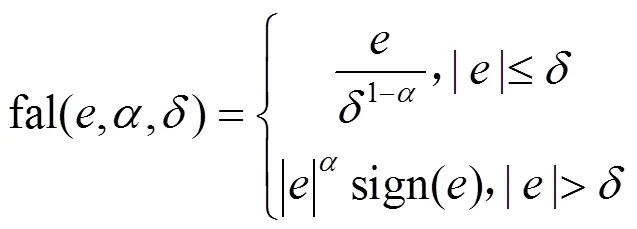
选择适当观测器参数01、02和03，ESO便能实现对式(10)中各个变量进行实时跟踪，即1→1、2→2、3→3。

2.2.3 LSEF组合方式设计

为减少控制器调节参数，状态误差反馈采用线性组合方式，如式(12)所示：

式中p、d分别为比例、微分系数。

根据图5可知，ADRC控制器输出量为

当总扰动估计值3能够在误差范围内跟踪总扰动，则对应输出为

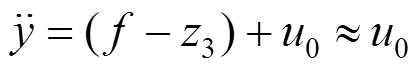
由式(14)可知，对总扰动观测准确也能使系统达到稳态，这样便能够避免积分环节对系统动态性能的影响。

2.3 PR控制器设计

根据式(7)可知，当三相负载呈现不平衡状态时，输出电压由直流分量和交流分量共同构成，为消除交流分量干扰，因此引入PR控制器。其对应的传递函数如(15)所示。

式中：k为比例增益；kR为谐振增益；ω0为基波角频率。取k=1，kR=1，ω0=628rad/s，图6为G(s)的伯德图。

通过在系统中加入一个无限增益来抑制系统中某种特定频率的信号是PR控制器一大特点，同时不会依赖系统中其他参数，这种控制方式相比其他控制方式更具有灵活性。但是理想PR控制器在所需要频率处增益为无限大，在实际中，无论是使用数字控制器还是模拟控制器，其增益都不可能为无限大。一方面，当增益太大时，容易引起系统不稳定；另一方面，理想PR控制器增益跌落非常迅速，很难处理电网电压和频率波动的情况。因此需要增大理想PR控制器对应的带宽，改进后PR控制器[14-15]如式(16)所示：

改进后PR控制器中取k=1，kR=1，w0= 628rad/s，ωc=50rad/s，将参数带入式(16)，画出其伯德图如图7所示。由图7可看出w0= 628rad/s处，即f=100 Hz处会产生较大增益，并且控制带宽有所增加，能够更好适应微电网频率波动。

改进PR控制器中比例增益的作用和PI控制器中一样，它能决定系统稳态性能和动态性能，改进PR控制器中谐振增益R能够影响PR控制器在谐振点处的增益，与理想PR控制器相比，式(15)中加入了一个参数c，其作用是可以通过截止频率c调整控制器增益和谐振点处带宽，使其控制范围能够更大。

3 仿真验证及分析

通过Matlab/Simulink对所提的ADRC+PR复合控制策略进行验证。仿真中系统各项参数如 表1所示，为验证所提控制算法能够应用于多种工况下，负载端包含三相平衡负载、三相阻性不平衡负载、三相阻感性不平衡负载以及三相阻容性不平衡负载，如表2所示。

表1 系统参数

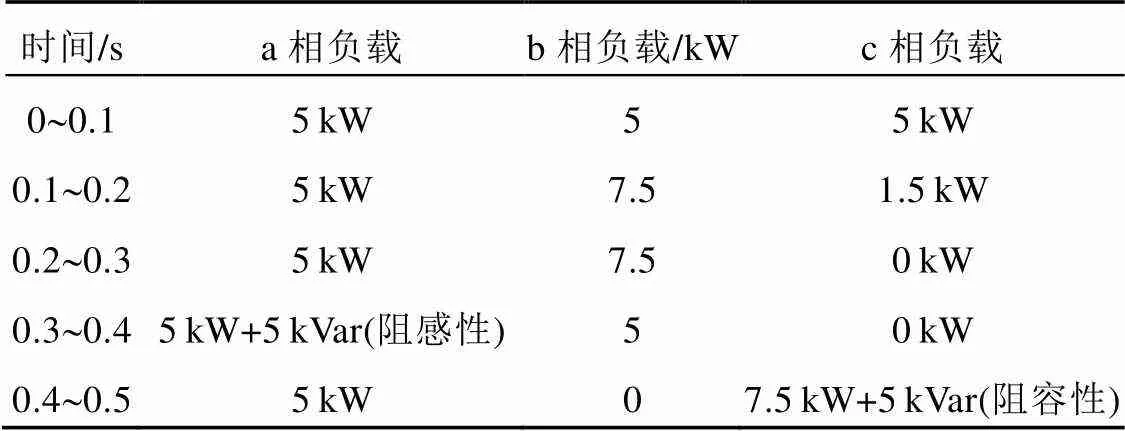
表2 负载切换工况

1）采用开环控制。

图8—10分别表示开环控制下的三相输出电压、三相输出电流和三相输出电压不平衡度。由图8和9可知，当负载处于平衡状态工况下，负载端输出电压和输出电流处于平衡状态，当负载端出现不平衡工况，输出电压和输出电流都会出现不平衡状态，在离网模式下，主要控制目标是输出电压，使得输出电压能够达到三相平衡状态。由图10可知，开环控制下负载端输出电压不平衡度最高时已超过12%，根据IEEE Std 112-1991标准，三相不平衡度波动范围为0~2%，短时间可以高于2%，但不能高于4%。由此可知，在平衡负载工况下，输出电压能够达到标准，但当负载处于不平衡状态时，开环控制输出电压不平衡度不能满足控制要求。

2）采用所提ADRC+PR控制算法。

ADRC+PR控制器参数如表3所示，负载工况与1）中工况顺序相同，图11为输出电压，图12为输出电流，图13为输出电压不平衡度。图11与图8进行对比可知，在表2不平衡工况下，图8不能使输出电压处于平衡状态，而从图11可以看出，在ADRC+PR控制器作用下，输出电压能够稳定在311 V；由图13可知，采用所提控制算法，输出电压不平衡度始终低于2%，满足IEEE Std 112—1991标准要求，可以说明所提控制策略有较好的控制效果；为了维持输出电压处于平衡状态，在不平衡负载工况下，图12中输出电流必然处于不平衡状态。

图8 开环输出电压

图9 开环输出电流

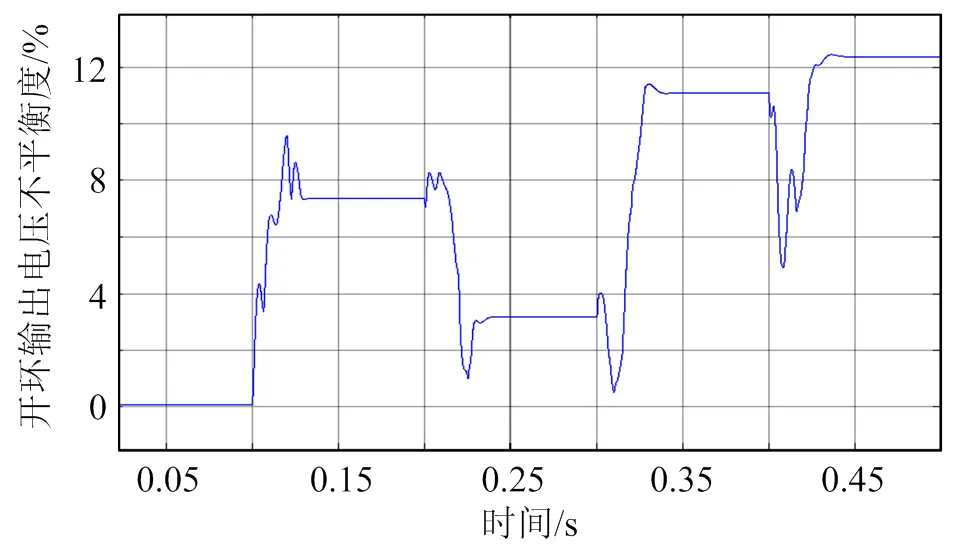
图10 开环输出电压不平衡度

表3 ADRC+PR控制器参数

图11 ADRC+PR输出电压

图12 ADRC+PR输出电流

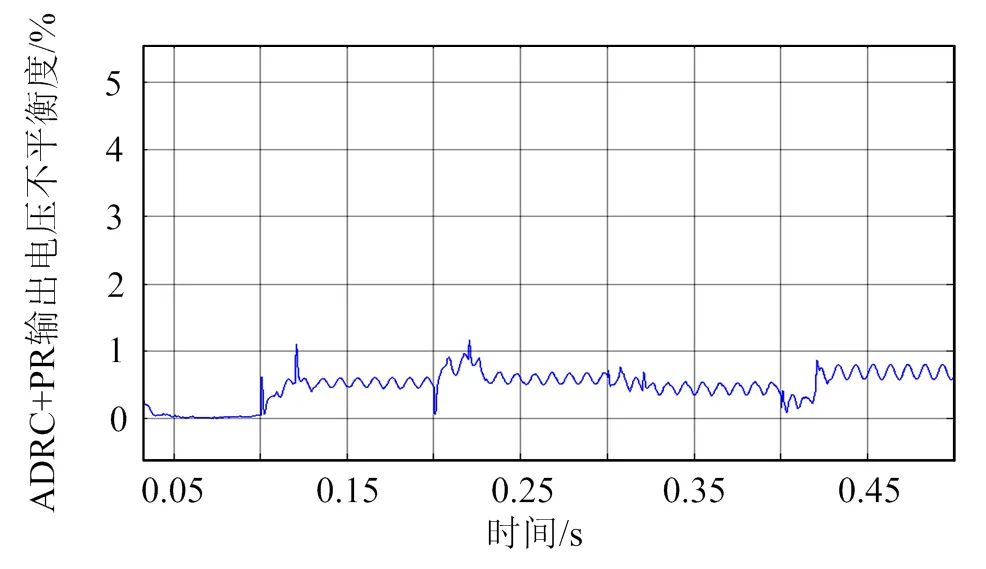
图13 ADRC+PR输出电压不平衡度

3）控制器结构为双环结构对比。

双环控制器的外环采用PI+PR控制器，内环采用PI控制器，与ADRC+PR控制算法的效果对比如图14所示，表4为对比控制器参数。在图14中0~0.2 s，2种控制器控制效果相差不大；0.2~0.5 s，在有一相负载开路、三相不平衡阻感性负载和三相不平衡阻容性负载工况下，ADRC+PR控制效果比双环控制好，可见所提ADRC+PR控制器适用范围更广。

4 结论

将ADRC控制器与PR控制器运用于电压单环控制策略中，能够针对不平衡负载对整个系统进行控制，不但可以减少电流检测元件，节省成本，而且适用范围更广。在三相平衡负载和不平衡负载等多种工况下进行了相应仿真验证，通过仿真结果可知，在多种工况切换下，三相四桥臂逆变器中三相输出电压不平衡度均满足国际标准，有效证明了所提复合控制策略的可行性及其优势。

图14 不同算法控制效果对比

表4 对比控制器参数

[1] Kukrer O，Komurcugil H，Doganalp A．A three-level hysteresis function approach to the sliding-mode control of single-phase UPS inverters[J]．IEEE Transactions on Industrial Electronics，2009，56(9)：3477-3486．

[2] 赵清林，许方玲，杨秋霞，等．基于LCL滤波器并网逆变器分裂电容控制研究[J]．太阳能学报，2016，37(4)：815-822．

[3] 裴雪军，刘明先，康勇．组合式三相逆变器并联控制技术研究[J]．电力电子技术,，2012，46(1)：99-101．

[4] 周啸，金新民，唐芬．0坐标系下带不平衡负载的三相四桥臂变流器控制策略[J]．中国电机工程学报，2014，34(19)：3105-3113．

[5] 谭翠兰，陈启宏，张立炎，等．三相四桥臂并网逆变器的无差拍重复控制[J]．电力系统自动化，2018，42(18)：142-154．

[6] 顾和荣，王德玉，沈虹，等．三相四桥臂逆变器控制技术研究[J]．电力系统保护与控制，2011，39(24)：41-46．

[7] 王恒利，付立军，肖飞，等．三相逆变器不平衡负载条件下双环控制策略[J]．电网技术，2013，37(2)：398-404．

[8] 赵云斌，李鹏程，尉怡青，等．不平衡畸变负荷无功功率理论分析与应用[J]．电测与仪表，2018，55(2)：1-7．

[9] 陈杰，赵冰，陈新，等．不平衡负载条件下三相四线制并联逆变器的下垂控制[J]．电工技术学报，2018，33(20)：4790-4801．

[10] 李德文，任旭虎，吕正阳，等．电网畸变下基于改进DSSOGI-FLL同步信号提取方法[J]．电测与仪表，2018，56(10)：40-46．

[11] 闫志强，雷霞，何建平，等．三相不平衡对配电变压器带负载能力的影响研究[J]．电测与仪表，2018，55(8)：51-57．

[12] 韩京清．从PID技术到“自抗扰控制”技术[J]．控制工程，2002(3)：13-18．

[13] 崔晓波，刘久斌，朱红霞，等．基于自抗扰Smith预估补偿方法的超临界机组再热汽温控制研究[J]．发电技术，2018，39(4)：367-372．

[14] 曾进辉，孙志峰，雷敏，等．改进型PR控制器应用于双馈风力发电系统[J]．电力电子技术，2019，53(2)：87-90．

[15] 玄兆燕，马振宇，景会成，等．基于改进重复控制与准比例谐振的电压型逆变器研究[J]．电力电容器与无功补偿，2018，39(6)：157-162．

Research on Three-phase Unbalance of Micro-grid Based on Active Disturbance Rejection Control

QIAN Mengran, LI Hui, LIU Xinxiu

(College of Automation Engineering, Shanghai University of Electric Power, Yangpu District, Shanghai 200090, China)

Under the condition of three-phase unbalanced load in micro-grid, three-phase four-leg inverter can solve the unbalanced three-phase output voltage because of unbalanced load. Nevertheless, in the0 synchronous reference frame, the output voltage and current of three-phase four-leg inverter are coupled with each other. If the load is unbalanced and the open-loop control is directly used in the0 synchronous reference frame, the output voltage is still unbalanced because of double frequency disturbance caused by unbalanced load. To solve these problems, this paper established the mathematical model of three-phase four-leg inverter, derived the open-loop transfer function of the controlled plant and deeply analyzed the mechanism of unbalanced output voltage of three-phase four-leg inverters. In addition, according to the system model information, a second-order active disturbance rejection controller (ADRC) controller was designed to decouple the voltage and current inaxis, and it could reduce the number of originals measured. Proportional resonant controller was introduced to eliminate the disturbance caused by 100 Hz. Finally, the effectiveness of the solution was verified by Matlab/Simulink.

micro-grid; three-phase four-leg inverter; unbalanced voltage;axis decoupling; active disturbance rejection controller (ADRC); proportional resonant controller

10.12096/j.2096-4528.pgt.19128

TM 711

上海市国际科技合作项目(15220710500)；上海市地方院校能力建设项目(15160500800)；上海市科委重点项目(18DZ1203200)。

Project Supported by Shanghai International Science & Technology Cooperation Program (15220710500); Shanghai Science and Technology Commission Local College Capacity Building Program (15160500800); Shanghai Science and Technology Commission Key Program (18DZ1203200).

2019-08-26。

(责任编辑 辛培裕)