基于新CH2(A′)势能面的C(3P)+H2(X1)→H(2S)+CH(2Π)反应量子波包动力学*

赵文丽 王永刚 张路路 岳大光 孟庆田

1)(山东农业大学信息科学与工程学院,泰安 271018)

2)(山东交通学院理学院,济南 250357)

3)(山东师范大学物理与电子科学学院,济南 250358)

基于一个最新的势能面,运用切比雪夫波包方法对初始态为反应体系在1.0—2.0 eV 的碰撞能量范围内进行了动力学研究.通过对角动量量子数J=60以下的所有分波进行计算,得到了反应几率、积分散射截面和速率常数.计算中用到了耦合态近似方法和考虑科里奥利耦合效应的精确量子方法.通过对比发现,随着角动量量子数以及能量的增加,科里奥利耦合效应的影响越发显著,因而对于该反应体系,科里奥利耦合效应不可忽略.本文计算所得的积分散射截面和速率常数尚无实验数据可以比较,对该反应的后续研究有一定的参考价值.

1 引 言

在燃烧化学[1]和天体化学[2,3]中,碳原子和氢分子间的反应是一种非常重要的化学反应,而CH2自由基作为中间产物,在这类碳氢反应中发挥着重要的作用[4].迄今为止,人们在实验[5-7]和理论[8-19]上对亚甲基分子CH2进行了大量的研究,且主要集中于等几个单态的势能面性质[8-11]和相关的的动力学计算而对于三态的势能面和相关的反应动力学研究相对较少,特别是正向反应少有涉及.本文的工作就是基于一个最新的CH2(X3A'')势能面并对反应开展量子波包动力学研究.

在理论方面,Knowles 等[20]在1983年给出了一个态的势能面,该势能面能较好地反映体系在所有渐近区的性质.基于该势能面,Murrell和Dunne[21]用准经典轨线(QCT)的方法研究了并计算了该反应的速率常数.1993年,Harding等[22]应用多参考组态相互作用(MRCI)[23,24]结合Dunning相关一致基组的方法得到了CH2基态的全维势能面(HGS).随后,该小组应用HGS计算了反应的速率常数,在高温区域(1500—2000 K),理论结果和实验符合得很好.基于 HGS,van Harrevelt等[25]应用量子波包和QCT的方法计算了 C H+H→C+H2的散射截面和速率常数.另外,Gamallo等[26]使用玻恩-奥本海默(BO)近似的量子力学方法对H(2S)+反应进行了动力学计算,并指出该反应只发生在解耦合的基态上.1996年,Guadagnini和Schatz[27]使用 QCT方法研究了 C(3P)+H2→H+CH 反应的产物分布,并指出产物 C H+H 的形成完全取决于C原子靠近H2的插入机制.

实验上,Scholefield等[28]使用激光烧蚀石墨的方法获得 C(3P)粒 子束,研究了 C(3P)与H2,HCl,HBr和CH3OH的反应,并指出产物CH的生成与反应物的转动态呈现明显依赖关系.1997年,Ehbrecht等[29]使用高能量(10 —180 eV)的C原子束与H2发生光化学反应,观测到了生成CH产物不同 电 子态辐射 带(2Δ -X2Π,2Σ--X2Π和并指出三种态可观测的能量范围不同.

在2019年,Zhang等[30]应用多参考组态相互作用方法(MRCI),采用包含Davidson修正的aug-cc-pVXZ(X=Q和5)基组计算得到的5285个能量点,将其外推到完备基组极限(CBS)并利用多体展开(MBE)的方法拟合构建了一个关于的全维解析势能面,其中势能最大值与最小值之间的跨度为17 eV,势能面的总方均根偏差为0.0349 eV.基于该势能面,该团队运用QCT方法,计算了反应的积分散射截面和速率常数,与基于HGS势能面的动力学计算结果和实验结果符合得很好,从而验证了该势能面的精确性.

CH2自由基电子态性质复杂,相关的动力学研究涉及到BO近似和非绝热过程,不过对该体系性质进行全面的研究并不是本文的目的.本工作主要是基于Zhang等[30]构建的势能面,用切比雪夫量子波包方法对反应的反应几率和散射截面等性质进行研究.本文所采用的方法,相对于传统的含时方法有着更优越的标度律,只需要波包的一次传播就能够给出所有能量点处的反应几率,并且波包在实空间的传播没有近似,因而在计算上更具有优势[31-33].本文主要包含以下几部分: 第二部分介绍所采用的理论方法以及相应的数值计算方法.第三部分给出理论计算结果和讨论.第四部分总结得出相关的结论.除特别说明之外,文中的所有公式和计算都使用原子单位.

2 理 论

对于反应物满足交换对称的体系(C + H2),使用雅克比坐标(R,r,γ)能够减少计算基组个数,在雅克比坐标下C + H2体系的哈密顿量的表达式为

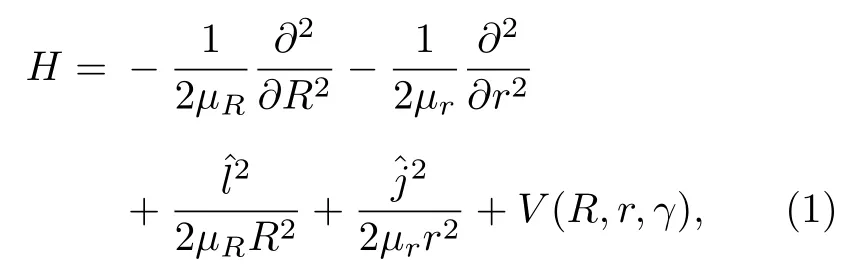
式中 r 表示双原子(H-H)之间的距离,R 表示碳原子与双原子质心之间的距离(C-H2),μr=mH/2和μR=2mCmH/(mC+2mH)表 示约化质量,V(R,r,γ)为体系的势能面,和是双原子转动角动量算符和轨道角动量算符.轨道角动量算符的平方可以表示为

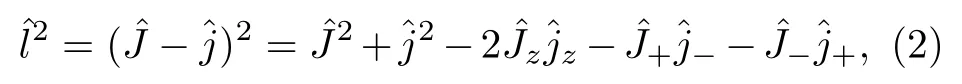
在切比雪夫波包方法中,波包传播的三项递归关系为[34,35]

其中,Hnorm=(H-H+)/H-是归一化的哈密顿量,且通过光谱的上(下)限计算获得[36].在 R(或 r)格点边缘,用高斯型函数D来描述输出波的边界条件

其中 dx决定阻尼范围,xd为阻尼起始点.初始波包|ψ0〉 表示为

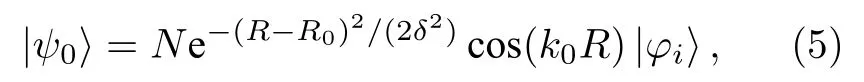
N 是归一化常数,k0为初动量,R0与δ 分别为初始波包的中心位置和宽度,| φi〉 为一个具体的振转本征函数.

通常S-散射矩阵元计算耗时较长[37],为了避免这种情况,本文采用流计算法,应用这种方法获得的初始态总反应几率为[38]

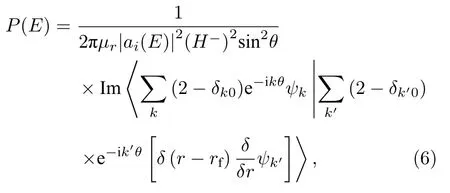
式中 rf决定了产物通道的分界面,θ≡arccos[(E-H+)/H-]是切比雪夫角,ai(E)是 初始波包的振幅[39]

为了获得给定初始态的积分散射截面(ICS),应该对所有J的反应几率进行求和

式中Ec为碰撞能量,是宇称为p、角动量量子数为 J 时,初始态的反应几率.将相应的积分散射截面 συiji(Ec)对碰撞能量 Ec结合玻尔兹曼权重进行积分,得到初态的速率常数为

其中f是电子的简并因子,kB和T分别为玻尔兹曼常数和热力学温度.

3 结果和讨论

3.1 势能面和最小能量路径

图1 CH2等势线,图中等势线间隔为0.1 eV(a)C沿着共线构型靠近H2分子;(b)C 沿着T构型插入H2Fig.1.Equipotential contour plot for CH2,the contour increments are 0.1 eV:(a)For bond stretching in C-H-H linear geometry;(b)for T-shaped insertion of C into H2 diatoms.

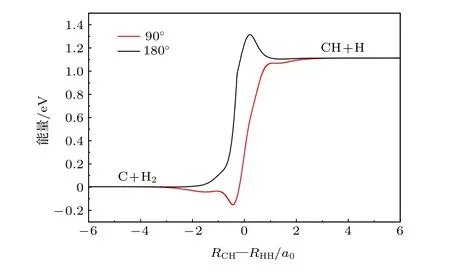
图2 90°和180°的最小能量路径Fig.2.The minimum energy paths as a function of RCHRHH at 90° and 180°.

3.2 计算细节

本文采用切比雪夫量子波包方法研究C(3P)+H2→H+CH反应.由上述分析可知,该反应是一个有较大的势垒和较小的势阱的典型吸热反应,为了计算得到精确的ICS和速率常数,需要较高的碰撞能量、大量的分波以及较大的基组数,尤其是考虑完全的CC效应时.对于 J=0 的情况,经过反复的收敛性测试,本文选取了最优的计算参数列于表1.应用这些计算参数,对于J=0,5,15,··,60的分波进行了CS 近似和完全的CC效应的计算,其他反应几率通过上述反应几率用三次样条插值法插值得出[42],进而得出碰撞能量范围在1.0—2.0 eV 的ICS,最后给出速率常数.

表1 波包计算中的数值参量(除特殊说明,均采用原子单位a.u.)Table 1.Parameters used in wave packet calculation(The atomic unit is used in the calculation unless otherwise stated).

3.3 反应几率

图3 不同分波的反应几率随着碰撞能量的变化Fig.3.The reaction probabilities vs.collision energy at different J.

图3给出了J=0,J=10,J=30和J=50的精确量子计算(考虑完全CC效应)反应几率随碰撞能量的变化.从图中可以看出,整体上反应几率数值较小(＜ 0.22),这是因为C原子无论从哪个角度碰撞H2,过程中都有可能形成中间络合物CH2,当能量较低、J较小时,络合物还可能比较“长寿”,并且CH2也有很大的几率衰变回反应物C+H2[27].图3中不同分波的反应几率显示范围是0—0.22,碰撞能量显示范围是1.0—2.0 eV.对于J=0,反应几率逐渐从0开始增大,约为1.10 eV时,反应几率大于0.1,这与前面MEP讨论的C(3P)+H2→H+CH反应是一个吸热反应是一致的,与该反应需要吸热1.109 eV也是一致的.但是同时要注意到,在1.0—1.1 eV的范围内,碰撞能量不足以越过该体系的势垒,而反应几率仍然不为0,这只能用量子隧穿效应解释.随着总角动量J的增加,离心势垒逐渐增大,反应阈能逐渐增加,J=30的阈能约在1.2 eV,J=50的阈能约在1.65 eV.从整体上看,反应几率随着碰撞能量的增加而增加,这也符合一般的吸热反应的反应几率变化规律.在低能区域反应几率呈现强烈的振荡,这是由体系的势阱(0.2 eV)所产生的共振引起的.当碰撞能量增加时,反应几率的振荡减弱,逐渐变得不明显.

在分子反应动力学的量子方法中,CS近似被广泛地应用于很多体系,而且这种方法已经被证明是相当成功的[43].但是,CS近似中忽略了科里奥利效应.实际上,有动力学研究表明在一些化学反应中,这种效应会产生非常重要的影响因而不能忽略[44,45].例如 Meijer和Goldfield[44]发现CC效应在H+O2反应中扮演着重要的角色,如果忽略CC效应将会使J ＞ 0时的计算变得不可靠,这种偏差在高能区越发明显.

图4画出了 J=5,10,20的 CS近似和CC两种方法下的反应几率.两种计算结果都表现出共振特性,随着J的增大,一些共振会消失,这是因为J越大,波函数计算中包含的分波更多.此外,CS的振荡幅度比CC的大得多,这是反应中科里奥利耦合效应受到长程力支配的结果.整体上来讲,在角动量J比较小的情况下(J=5),CC计算的反应几率小于CS近似的数值;当J=10时,两种方法的反应几率基本符合;当J=20时CC计算的反应几率大于CS近似的结果,J越大,二者差别越明显.从J较大时的单一分波来看(J=20),在低能区域(小于1.3 eV),CS的计算结果比CC的大,在1.3—2.0 eV的范围内,CC计算的结果大于CS近似的数值,并且碰撞能量越大偏差越大.理论认为,中间络合物CH2的形成对于反应机制起着主导作用.当J较小时,CS近似下由于H2分子态的限制,C更容易与其发生碰撞,从而促进产物生成,所以CS的几率较大.随着J的增大,更多分波贡献被考虑其中.一方面,CS近似下长程相互作用影响较大,长程势会使得碰撞时间变长,原子的重新组合变慢从而使得反应几率变小;另一方面,由于科里奥利耦合效应激发的振动模式更有利于破坏H-H键从而促进产物的形成.这种情况下,CC效应就会显著影响反应过程,所以CC的几率较大.

3.4 积分散射截面和速率常数

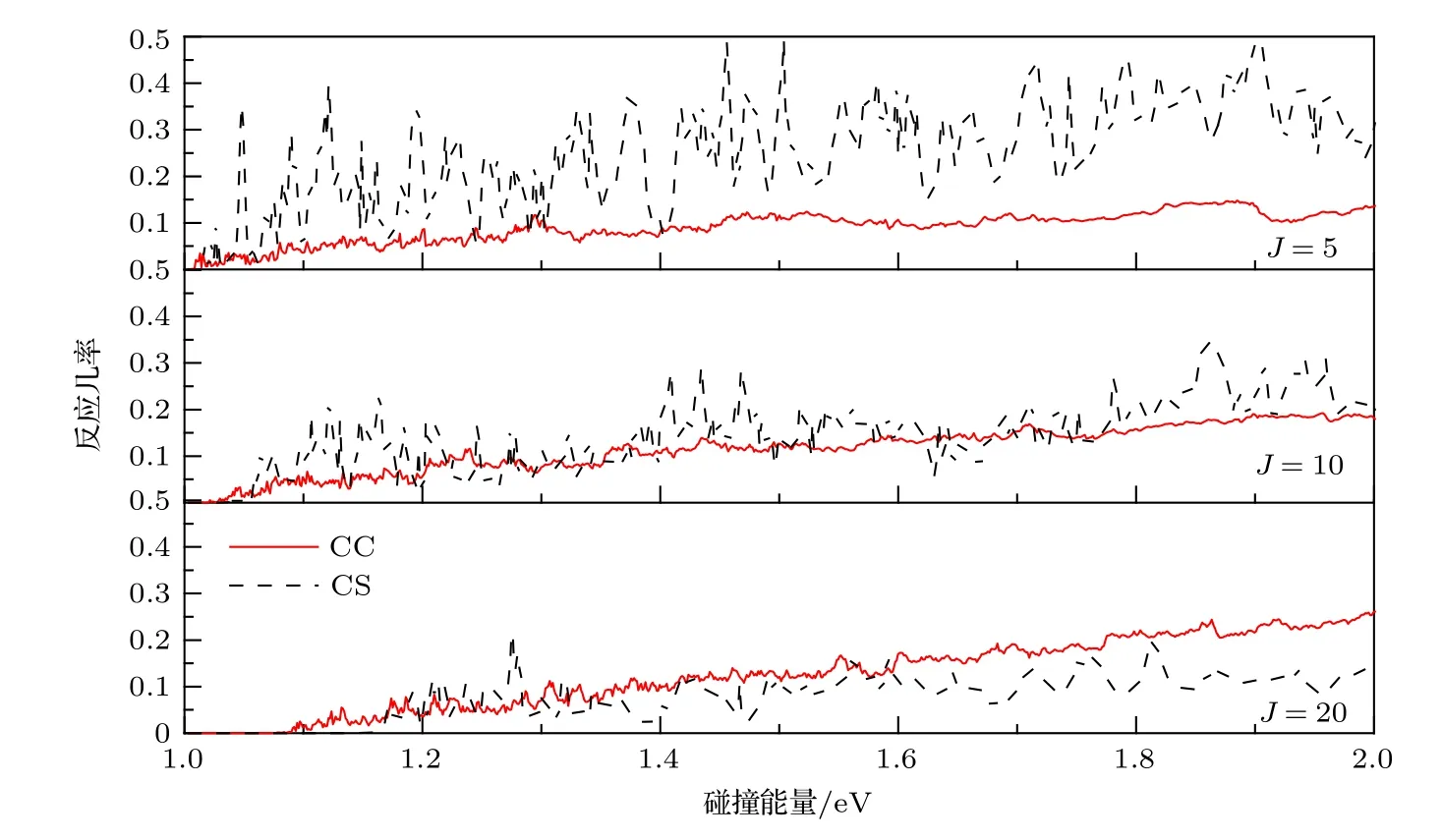
图4 CC与CS反应几率比较Fig.4.Comparisons between the CC and CS probability.

根据(8)式,ICS是把所有分波的反应几率乘以各自权重,然后再对所有的分波求和得到的.在1.0—2.0 eV的碰撞能量范围下,我们对所有J ＜ 60分波进行加权求和得到了 C(3P)+H2→H+CH 反应的ICS.图5给出了分别用CS近似和CC方法得到的ICS随着碰撞能量的变化.从图中可以看出,随着碰撞能量的增加,两种计算方法的ICS都会增加,与一般吸热反应的ICS的变化趋势一致.相比于CS近似的ICS,CC计算的结果振荡得更加剧烈,但幅度比CS的小,并且CC的ICS随碰撞能量的增加而增加得更快.当EC＜ 1.27 eV时,两种方法的计算结果基本符合.当EC＞ 1.27 eV时,CC的ICS迅速增加,CS的ICS则缓慢增加,碰撞能量越高,二者的差距越大.例如,当EC=1.21 eV 时,σCC=0.135 Å2,σCS=0.130 Å2,二者数值几乎相当;当EC=1.61 eV时,σCC=0.647 Å2,σCS=0.256 Å2,前者是后者的 2.53 倍;当EC=1.99 eV 时,σCC=1.022 Å2,σCS=0.305 Å2,前者是后者的3.35倍.考察势能面的特征就会发现,势能面的势阱、鞍点和过渡态的位置对于中间络合物的形成是非常有利的,即不利于产物的形成,这就导致了CS近似下ICS随能量增加而缓慢攀升,然而,正如前文所述,科里奥利耦合效应就可以克服这一点,所以CC的ICS随能量增加上升得非常快.

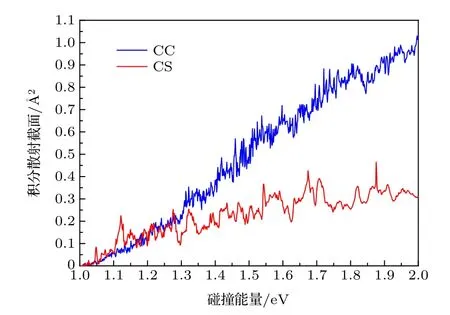
图5 C+H2反应的积分散射截面Fig.5.The integral cross section of the C+H2 reaction.

基于积分散射截面,应用(9)式,我们计算出了 C(3P)+H2→H+CH 反应的速率常数,如图6所示.温度的取值范围为1000—2000 K,对应ICS碰撞能量的取值范围1.0—2.0 eV.图中红色实线表示CC计算的速率常数,黑色虚线表示CS近似的结果.从图6中可以看出,在1000—1400 K,速率常数增加比较平缓,CC和CS的结果基本相一致;当T ＞ 1400 K时,随着温度的增加,速率常数迅速增加,我们认为速率常数对于温度如此敏感归因于该反应为吸热反应,有较高的反应阈能.另一方面,我们注意到文献[46]报道的类似电子结构O(3P)与CH4反应的速率常数,该文献认为计算过程中忽略势垒交叉的影响会导致速率常数计算结果偏大.基于同样的原因,我们预测本文速率常数计算结果可能比实际偏大.此外,类似于ICS的结果,随着温度的增加,CC速率常数比CS攀升得更快,例如在T=1400 K时,CC计算和CS近似的速率常数分别为 5.52 × 10—15和5.07 ×10—15cm3·molecule—1·s—1,二者的差值为4.50 ×10—16cm3·molecule—1·s—1,CS 比 CC 结果小 8.25%;在T=1700 K时,CC计算和CS近似的速率常数分别为 2.91×10—14和2.37×10—14cm3·molecule—1·s—1,CS比 CC结果小 18.58%;在 T=2000 K时,CC计算和CS近似的速率常数分别为9.43 × 10—14和6.98 × 10—14cm3·molecule—1·s—1,二者的差值为2.46 × 10—14cm3· molecule—1· s—1,CS 比 CC 结果小25.95%.可见,温度越高,CC与CS的计算结果差别越大.

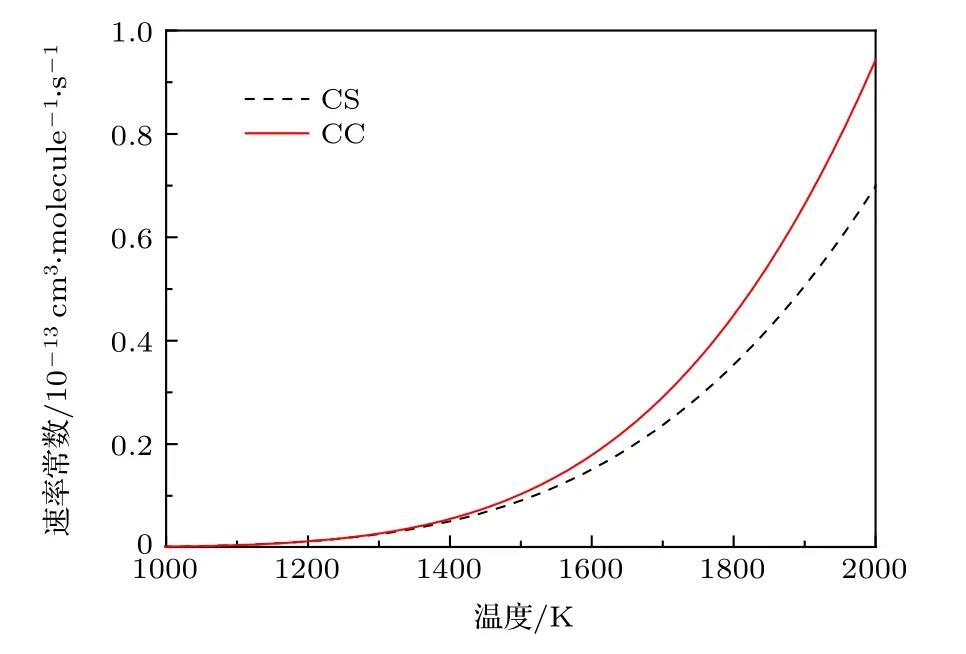
图6 C+H2反应的速率常数Fig.6.The rate constant of the C+H2 reaction.

4 结 论