步进频率信号在目标成像中的速度补偿研究

张 恒，宋 佳，柯 涛

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

步进频率雷达信号是均匀步进的脉冲序列，波形相参且带宽窄[1]。一组脉冲序列可以等效地获得宽带信号，具有分辨力高的特点，有利于目标的高分辨一维距离成像。这种大带宽信号的优势可以降低对前端收发组件性能、AD采样器件和后端信号处理瞬时带宽的需求，是一种热门的雷达信号波形，在毫米波成像、高速目标检测、雷达导引头和汽车避碰等军用、民用领域有着广泛的应用。步进频率雷达信号成像周期长，对多普勒敏感，动目标会产生距离像畸变和移位，实际使用时必须对高速目标的速度进行精确补偿。针对以上问题，本文对目前较为热门的几种高速目标速度补偿方法进行了理论分析和仿真，并提出了一种较为有效的速度补偿方法。

1 步进频率雷达信号分析

步进频率雷达信号的时域波形如图1所示。

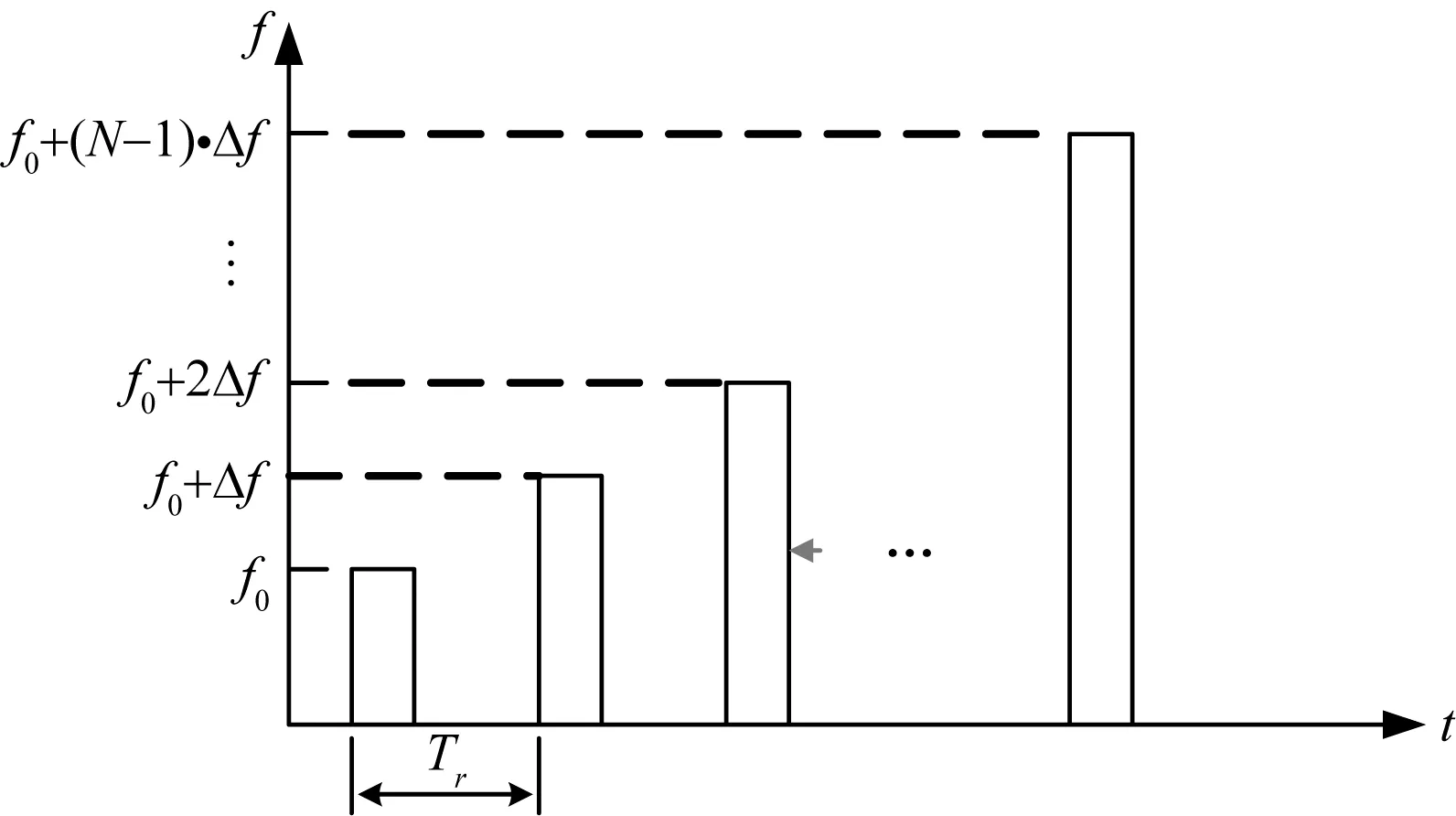
图1 步进频率雷达信号波形示意图

步进频率信号表达式如下：

exp[j(2π(f0+iΔf)t)]

(1)

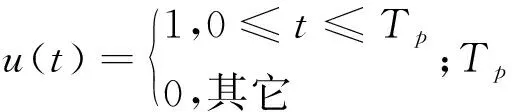
根据雷达模糊函数公式，求得x(t)模糊函数为：

|χ(τ,fd)|=

(2)

式中：Δf=10 MHz；N=10；Tp=0.5 μs；Tr=2 μs。信号模糊图仿真如图2所示。

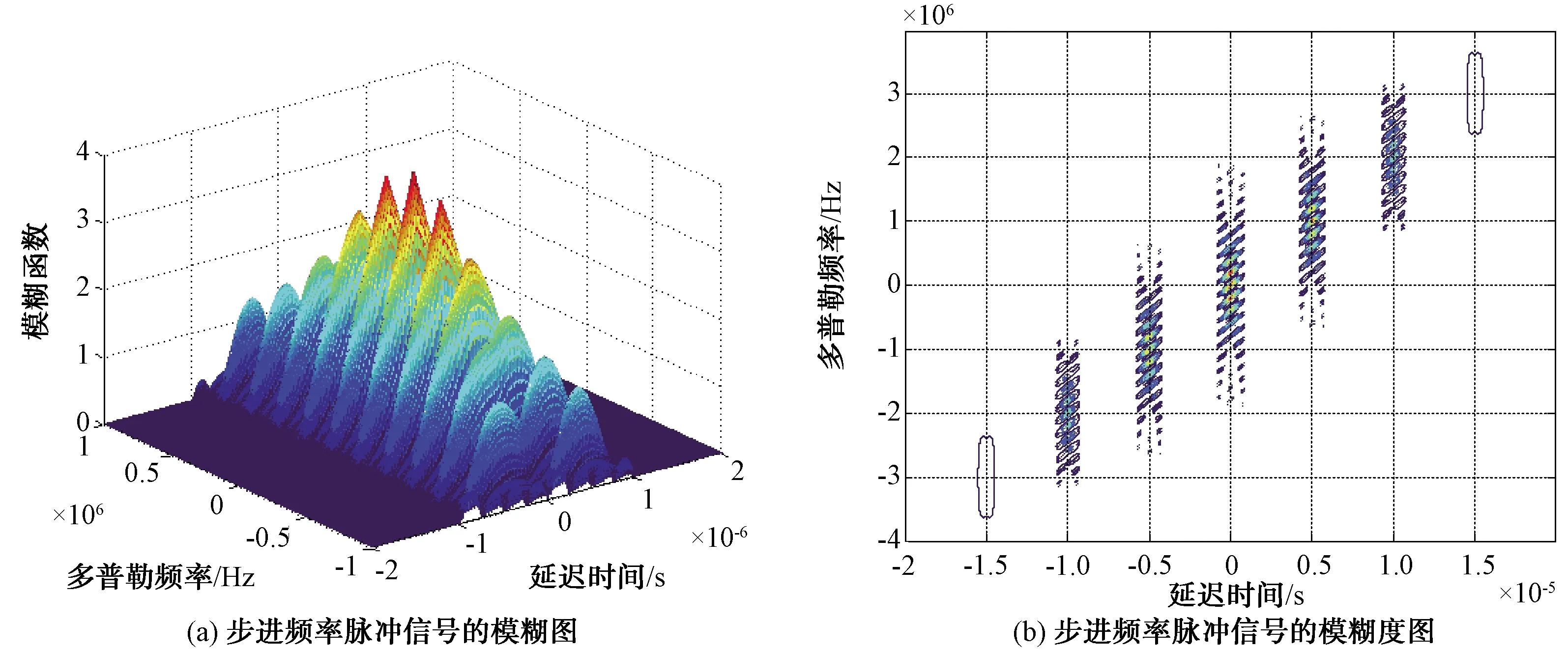
图2 模糊图和模糊度图仿真

模糊图由彼此不重叠的模糊带组成，具有周期性，此回波信号存在时频耦合和速度/距离模糊的特性[2]。

2 速度对目标成像的影响

对于运动的目标，讨论速度和目标一维距离成像的关系。设采样时间t=iTr，有R(t)=R-viT，代入式(1)得到步进频率雷达信号的回波为：

(3)

对上式进行分析：前2项表达式和固定目标是相同的，不会对目标成像造成影响，而后2项表达式内均含有速度分量v。

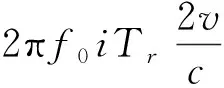
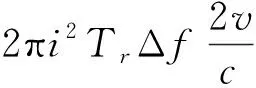
图3仿真了目标速度对运动目标距离成像的影响。仿真参数如下：载频20 GHz，脉冲重复周期Tr=20 μs，脉冲串宽度2 μs，Δf=10 MHz，频率步进点数N=32，4个目标在1 km处的运动速度分别为0 m/s、15 m/s、30 m/s和54 m/s。

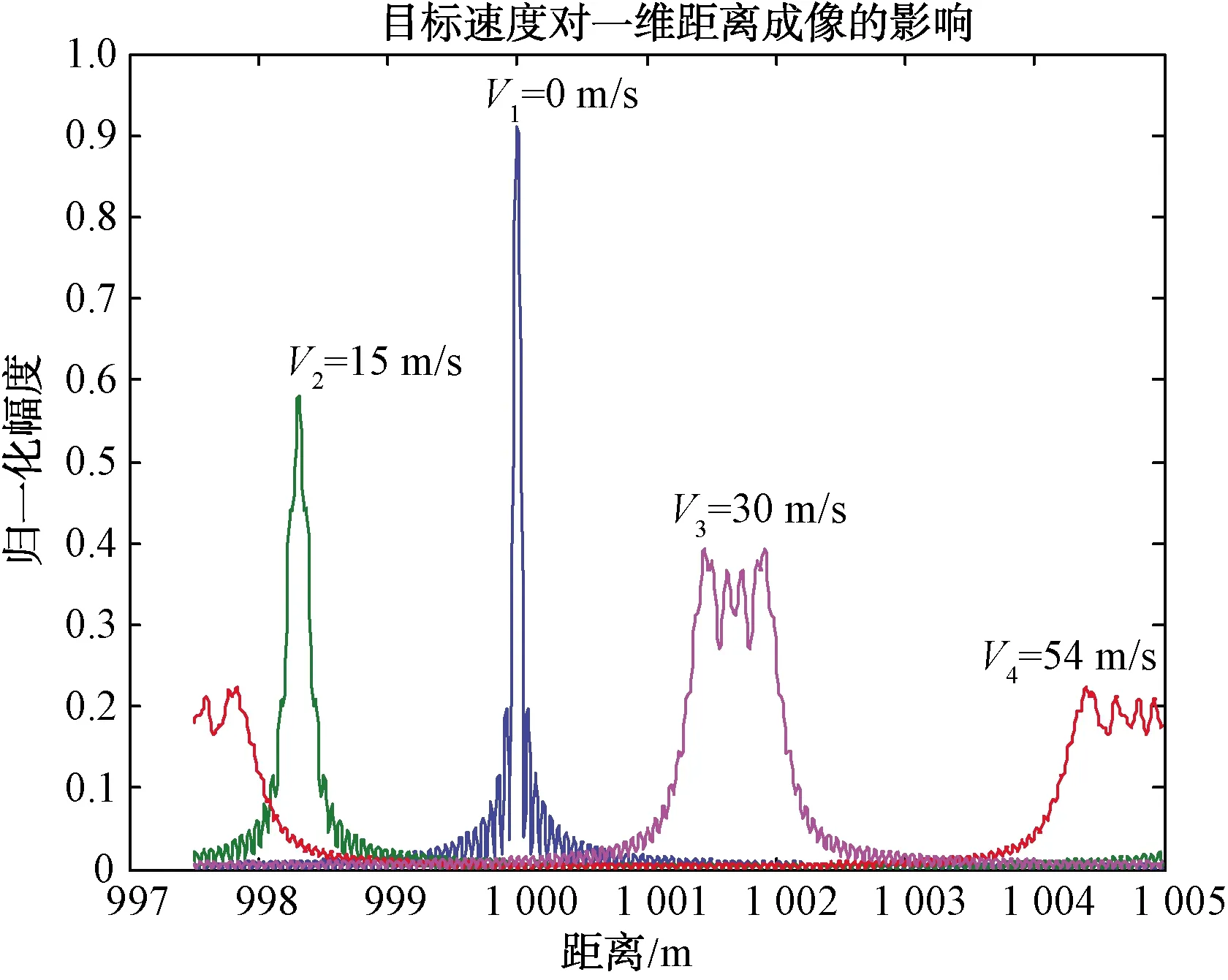
图3 速度对运动目标一维距离成像的影响

从仿真图能够直观地看出，目标速度对距离成像的影响和理论分析基本一致。目标速度V1=0 m/s时，一维成像的距离较准确；目标速度V2=15 m/s时，造成了一维成像的距离游走，导致目标测距出现误差；目标速度V3=30 m/s时，成像幅度出现畸变和展宽，恶化了SNR，不利于后端检测；目标速度V4=54 m/s时，目标距离分裂，且随着速度增加，目标分裂更加严重。

根据上述仿真和分析，对目标进行速度补偿后，才能得到高精度的一维距离成像。

3 步进频率雷达信号速度补偿方法研究

步进频率雷达信号速度补偿的基本思路是：首先使用基于时域互相关函数FFT的速度粗估计，将目标速度限定在一个大致范围，然后将粗估计速度代入脉组函数，精确搜索得到目标的准确速度估计[3]。

3.1 步进频率雷达信号的速度粗补偿

步进频率雷达信号采用一组正负频率步进脉冲串波形，首先步进频率雷达信号脉冲串从f0步进到f0+(N-1)Δf，然后脉冲串从f0+(N-1)Δf负向步进到f0[4]，脉冲串宽度和周期相同。则相邻2组脉冲串同位号的时域互相关函数为：

(4)

式中：第1项为常数。

因此对S12(i)归一化后做FFT运算，可得：

(5)

式中：η=Round(2N2vΔfTr/c)

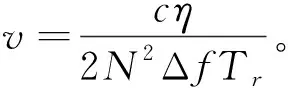
3.2 步进频率雷达信号的速度精确补偿

为了更精确地估计目标速度，在时域互相关速度粗估计的基础上，继续采用脉组函数的方法来对目标的速度精确搜索。目前比较热门的脉组函数方法主要有以下3种。

3.2.1 最小脉组误差法进行速度估计

目标速度的精确搜索原理就是：基于最小脉组误差函数收敛准则，搜索到全局速度收敛点，函数如下[5]：

(6)

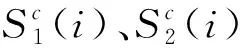
当Δv=0时，此函数具有全局最小值，Ps(Δv)=0，因此可通过在Δv范围上对Ps(Δv)进行最小值的搜索得到运动目标速度的精确估计。

3.2.2 最小脉组相位差分法进行速度估计

目标速度的精确搜索原理就是：基于最小脉组相位差分函数收敛准则，搜索到全局的速度收敛点，函数如下：

(7)

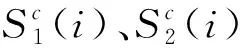
同理，当Δv=0时，Ps(Δv)=0。因此可通过在Δv范围上对Ps(Δv)进行最小值的搜索得到运动目标速度的精确估计。

3.2.3 最大脉组乘积求和法进行速度估计

目标速度的精确搜索原理就是：基于最大脉组乘积求和函数收敛准则，搜索到全局的速度收敛点，函数如下：

(8)

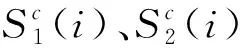
可知当Δv=0时，Ps(Δv)取得最大值，在Δv范围上对Ps(Δv)进行最大值的搜索即获得与目标真实速度相等的估计。

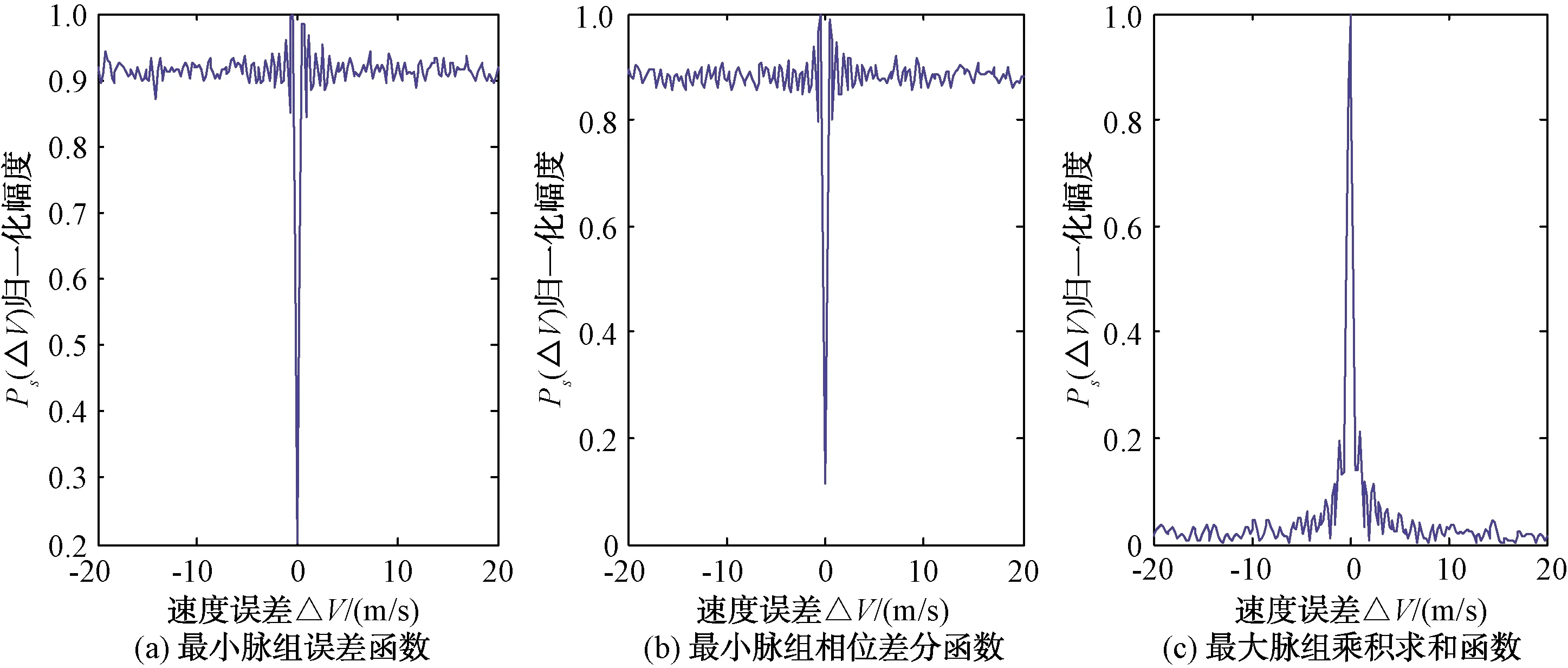
图4 3种脉组函数仿真

对比3种脉组函数仿真图可以看出，函数的峰值宽度相对较小，十分适合精确的速度估计，实际应用时搜索长度最好不超过各峰值宽度[6]。

4 仿真及分析

仿真中取载频20 GHz，Tr=20 μs，脉宽2 μs，频率步进Δf=10 MHz，频率步进点数N=32，目标的运动速度从0 m/s增加到100 m/s。考虑到实际处理时，不可避免地存在噪声和杂波信号，仿真时信号叠加高斯白噪声。

首先对目标的速度进行粗估计。如图5所示，在不同的信噪比和FFT点数的情况下对目标速度粗估计进行仿真。

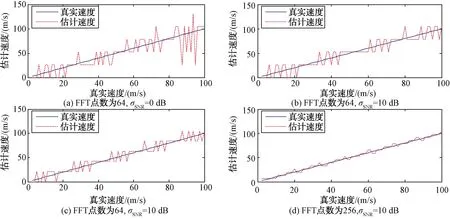
图5 时域互相关法对速度粗估计

由图5可以看出，通过增加FFT点数和提高信噪比(SNR)，可以有效提高速度粗估计的精度。在256点FFT和信噪比20 dB的情况下，速度粗估计误差在6 m以内。

对3种脉组函数精确速度估计的收敛性进行对比分析，在不同的信噪比条件下，完成蒙特卡洛仿真，给出估计速度误差，目标速度搜索范围为-5 m/s～5 m/s，图6给出了误差对比结果。

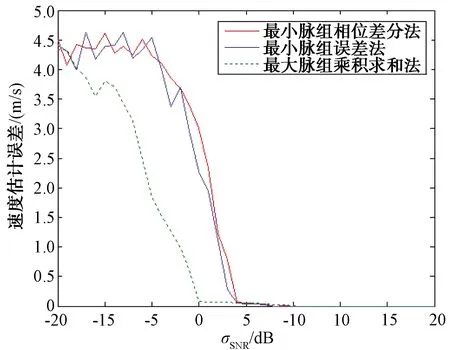
图6 3种脉组函数精确速度估计的收敛性比较

由图6可以看出，随着SNR增加，3种估计方法的收敛性差异不大，但是在σSNR=-5 dB时，最大脉组乘积求和法仍能够使速度估计有效地收敛至目标真实速度。此时其它2种函数速度估计收敛性相比较差，且只有在σSNR大于0 dB后，速度才能有效收敛到真实速度。因此最大脉组乘积求和法优势更明显。

假设有3个目标，距离和速度分别为：R1=500 m(速度V1=5 m/s)，R2=508 m(速度V2=15 m/s)，R3=505 m(速度V3=50 m/s)，采用最大脉组乘积求和法对3个目标进行速度精确估计和补偿，如图7所示。速度补偿后3个目标的最终成像效果良好，有效消除了目标的幅度下降和峰值分裂现象。

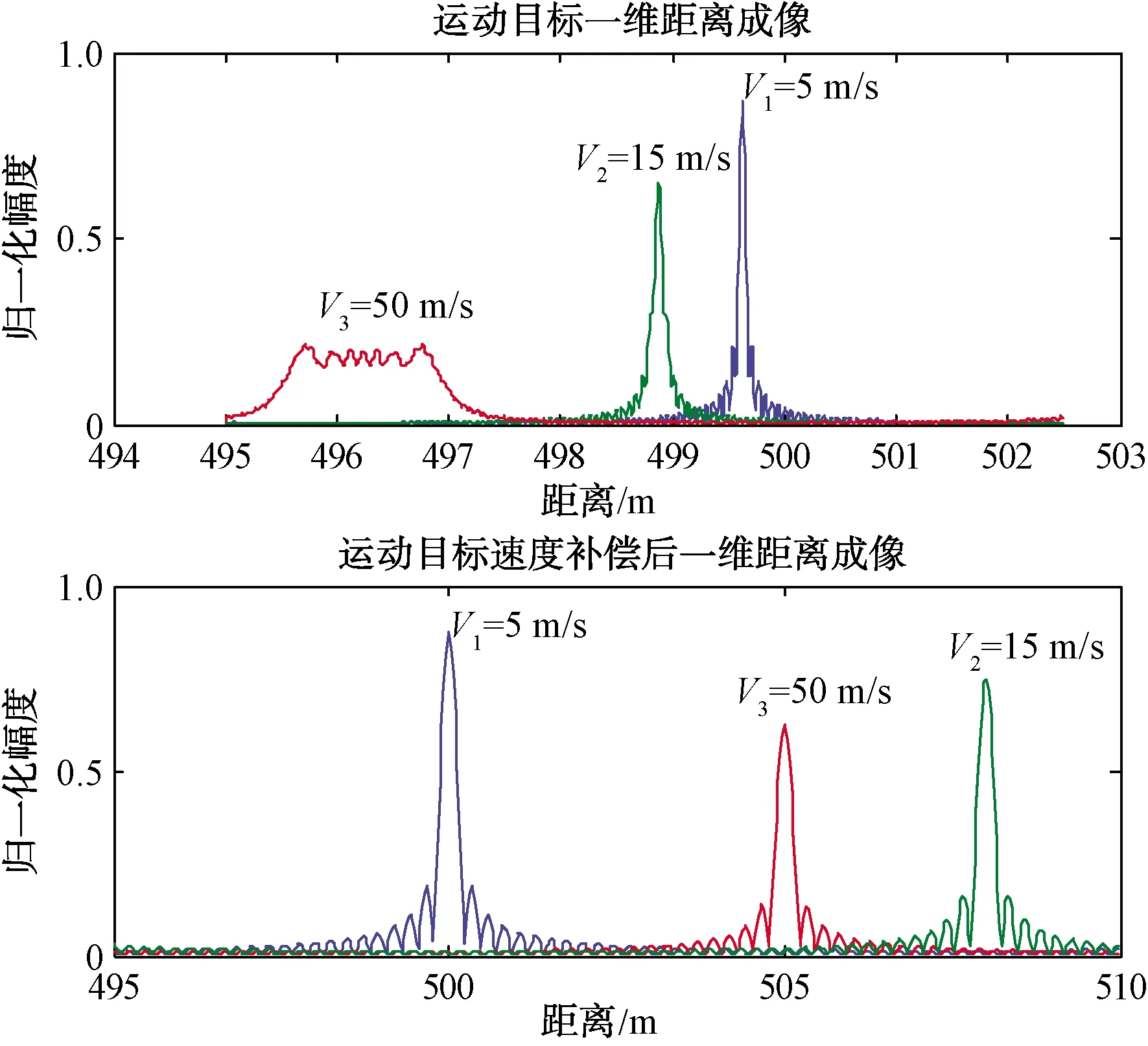
图7 速度精确补偿前后一维距离成像对比

5 结束语

速度补偿是步进频率信号目标一维成像必须解决的问题，本文通过理论分析和仿真实验对目标成像中的速度补偿方法进行了研究。首先使用基于时域互相关FFT法对速度粗估计，然后利用3种脉组函数高精度估计速度，最后对速度补偿后再完成距离成像。仿真结果表明3种脉组函数均能有效得到运动目标的真实速度估计，且最大脉组乘积求和法相对更具优势。