基于扩展卡尔曼滤波的二维弹道修正弹制导算法研究
2020-04-27何子达王亚飞王海川
何子达,王亚飞,王海川
(江苏自动化研究所,江苏 连云港 222006)
0 引 言
随着现代战争在远程精确打击方面的需要,将弹道探测及控制技术应用于常规炮弹的弹道修正弹应运而生。固定鸭舵二维弹道修正弹作为介于榴弹炮和导弹之间的一种制导炮弹,比榴弹炮射程远、命中精度高,比导弹成本低,在现代化战争中扮演着越来越重要的角色。
落点预测是弹道修正控制技术研究的重点部分,文献[1]采用扩展卡尔曼滤波对攻角修正系数进行评估,并根据攻角修正系数确定了四自由度弹道模型;文献[2]基于模糊控制理论和动态径向基函数(RBF)神经网络在线辨识理论,提出落点预测导引律;文献[3]给出了一种综合抛物线拟合、最小二乘法、非线性滤波等算法的落点预测方案;文献[4]以修正机构纵横向最大修正能力之比为比例因子,改进了滚转角的计算;文献[5]基于摄动理论和逐次逼近优化方法,建立了参考弹道和发射条件的快速求解方法;文献[6]研究影响落点预测精度主要因素;文献[7]剔除异常值提高落点预测精度。
之前的研究人员在对弹道积分初始点做滤波估计时,往往考虑的是使用无控弹道模型滤波估计。而二维弹道修正能力较弱,在大部分情况下都是处于有控状态飞行,这时如果依旧利用无控弹道方程滤波估计会带来一定的误差。本文基于有控质点弹道模型,利用扩展卡尔曼滤波算法,对一条有噪声的弹道进行滤波估计,得到当前时刻的状态估计值,选取快速积分算法,以滤波估计值作为积分初始点,外推弹道得到预测落点,并依据预测落点得到指导指令,最后通过仿真实验验证该算法的可行性。
1 固定舵二维弹道修正弹制导流程
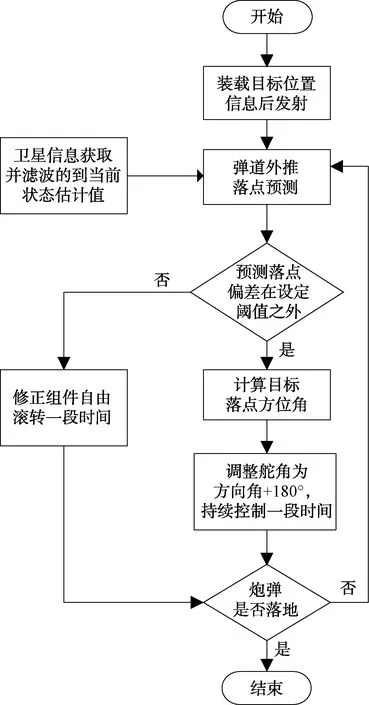
图1 二维弹道修正弹制导控制流程图
2 数学模型
2.1 弹道模型
由固定鸭舵二维弹道修正弹的工作原理可知,在弹道修正指令计算的过程中,弹道滤波、落点预测及指令解算环节均发挥着重要的作用,而弹道模型是进行弹道滤波及落点预测的基础。二维弹道修正弹的控制对制导指令解算的快速性和实时性具有较高的要求,现阶段弹载计算机运算能力有限,难以满足快速解算七自由度刚体弹道的需求,而常规的质点弹道模型又忽视修正组件控制效果的影响,无法对有控弹道进行解算。故本文在常规无控质点弹道滤波方程基础上引入控制量,建立二维弹道修正弹有控滤波模型[8]:
(1)
(2)
(3)
bx*=(bx-kxd)/cosθ0
(4)
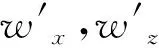
选取状态量为地面坐标系下的位置、速度分量:
X=[x,y,z,vx,vy,vz]T
(5)
可以得到状态方程:
(6)
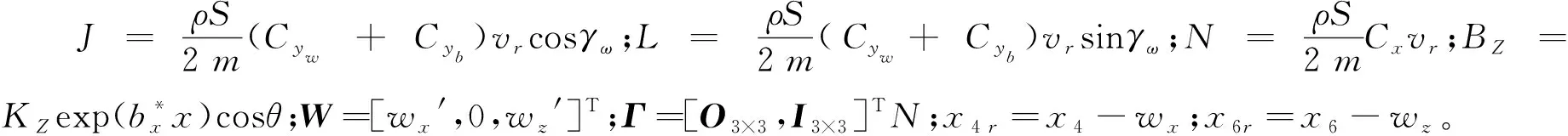
2.2 GPS量测模型
二维弹道修正弹在飞行中是通过弹载计算机GPS接收模块接收卫星信号,从而得到弹丸当前的位置、速度信息。因此可选取卫导测量得位置速度等信息构建观测矢量[10]:
那如果孩子觉得被欺负了,怎么办?对于学龄孩子可以参考我们之前发表过的一篇文章(《怎样的孩子容易被霸凌,怎样的会霸凌人?》)的建议,而对于学龄前的宝宝,你需要给他选择一些简单的做法,而不是像那种“打得过就打,打不过就跑”这种粗糙模糊的建议,对于他们这过于复杂了。
y=h(X)+ν=[x1,x2,x3,x4,x5,x6]+ν
(7)
式中:ν为GPS量测噪声误差,ν~N(0,R)。
2.3 扩展卡尔曼滤波算法
扩展卡尔曼滤波算法的原理是:对非线性状态方程以及观测方程进行局部泰勒展开,得到近似线性方程,然后利用传统的离散型卡尔曼滤波方程递推状态估计量。
对式(6)利用泰勒展开得到线性化后的离散方程:
(8)
扩展卡尔曼滤波的递推方法如下:
(1) 一步状态预测方程:
(9)
(2) 一部预测均方误差:
(10)
(3) 滤波增益矩阵:
(11)
(4) 状态估计方程:
(12)
(5) 估计均方误差方程:
(13)

2.4 制导指令的解算
根据扩展卡尔曼滤波算法,得到弹道的状态估计值后,即可以此为起始点,利用弹道积分算法外推无控弹道,得到预测的无控落点(xP,zP)。基于质点弹道模型的无控弹道快速积分算法在多篇文献中已有阐述,本文不再赘述。根据无控落点与目标点(xT,zT)的距离偏差,即可进行控制指令的解算。
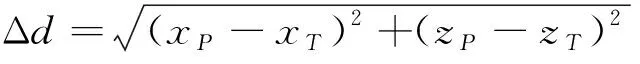
(1) 若Δd≤D
此时,无控落点与目标点位置较为接近,无需对弹道进行修正控制,即可得到较高的落点精度。因此,该情况下可使执行机构保持自由滚转状态,直至下一个预测周期。
(2) 若Δd>D
此时无控弹道落点与目标点偏差较大,须对弹道进行修正控制。由式(14)可知,修正落点相对于无控落点的方位角与控制角度的相位差约为180°,因此,固定舵滚转角指令可通过下式进行计算[11]:
(14)
3 仿真结果
3.1 扩展卡尔曼滤波仿真
对固定舵二维弹道修正弹进行弹道仿真,为使仿真结果和实际飞行情况尽量一致,结合实弹飞行试验结果,对弹药的气动力系数及力矩系数进行了离线辨识。为了模拟初速、射角、射向、气动力参数、风速等因素对弹道的影响,在七自由度弹药仿真中叠加了多类正态分布的随机误差,主要误差取值范围如表1所示。
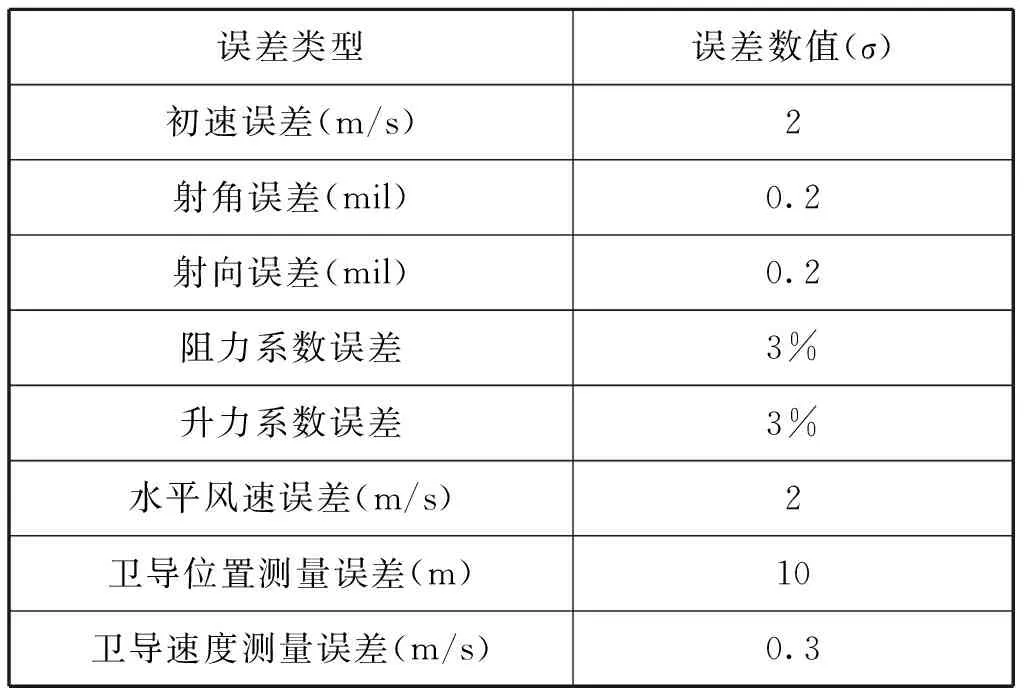
表1 随机扰动数值
仿真条件为:初速度850 m/s,射角48°,卫星导航数据率为10 Hz,令固定舵自飞行15 s后,始终保持固定舵修正机构滚转角为45°的施控状态,直到弹丸落地,对全弹道滤波,选取15 s~25 s,如图2~图4所示。
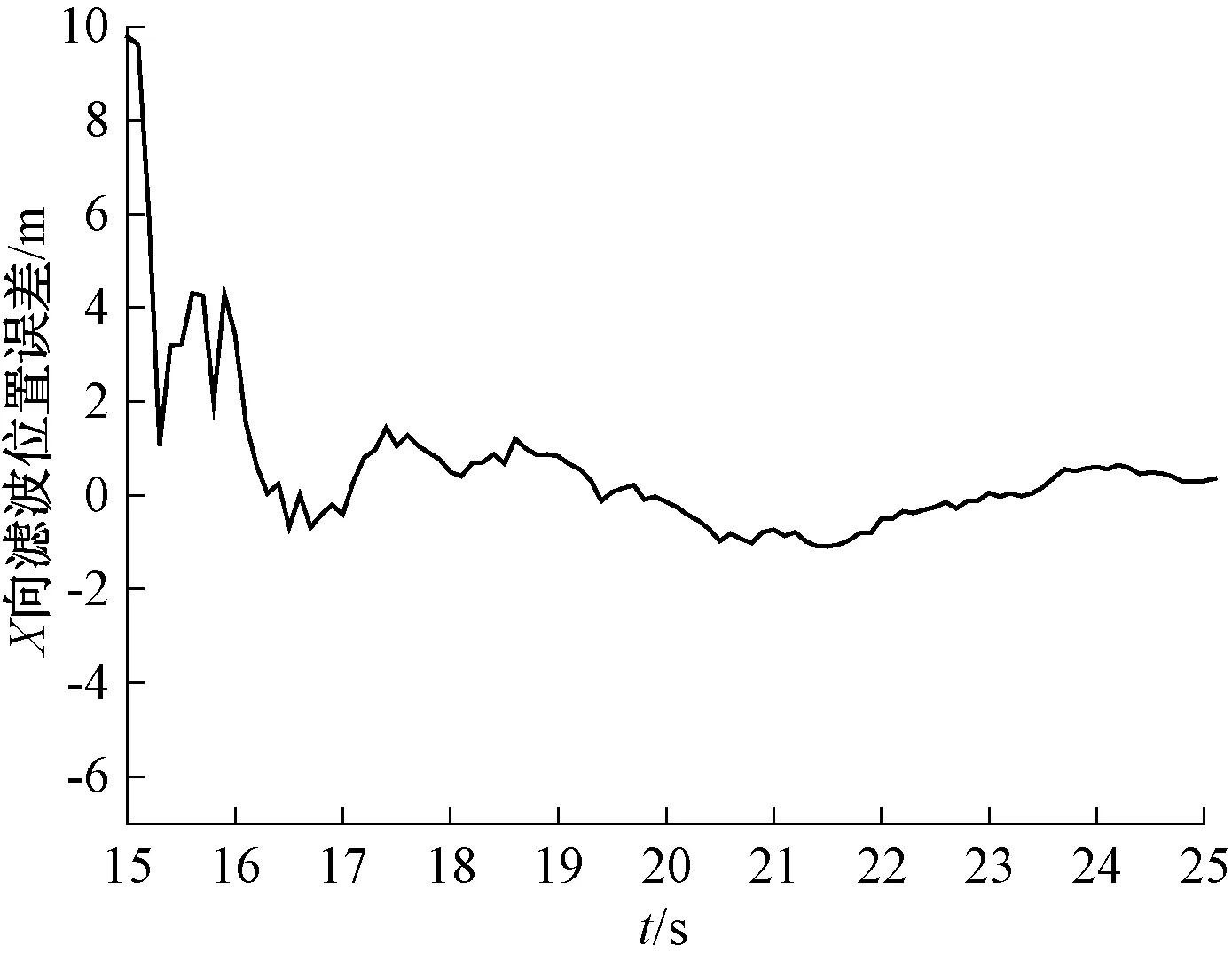
图2 X向位置估计误差
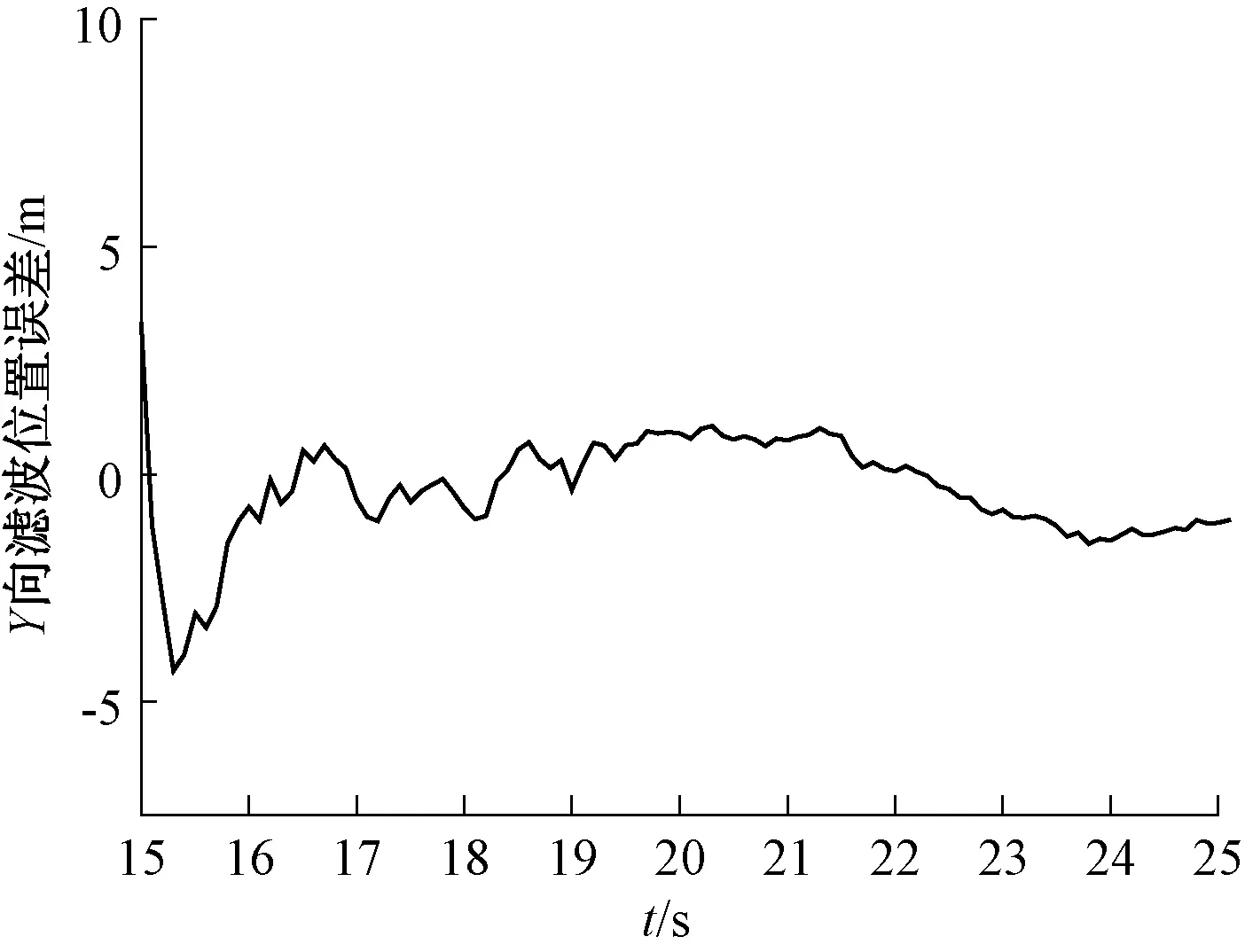
图3 Y向位置估计误差
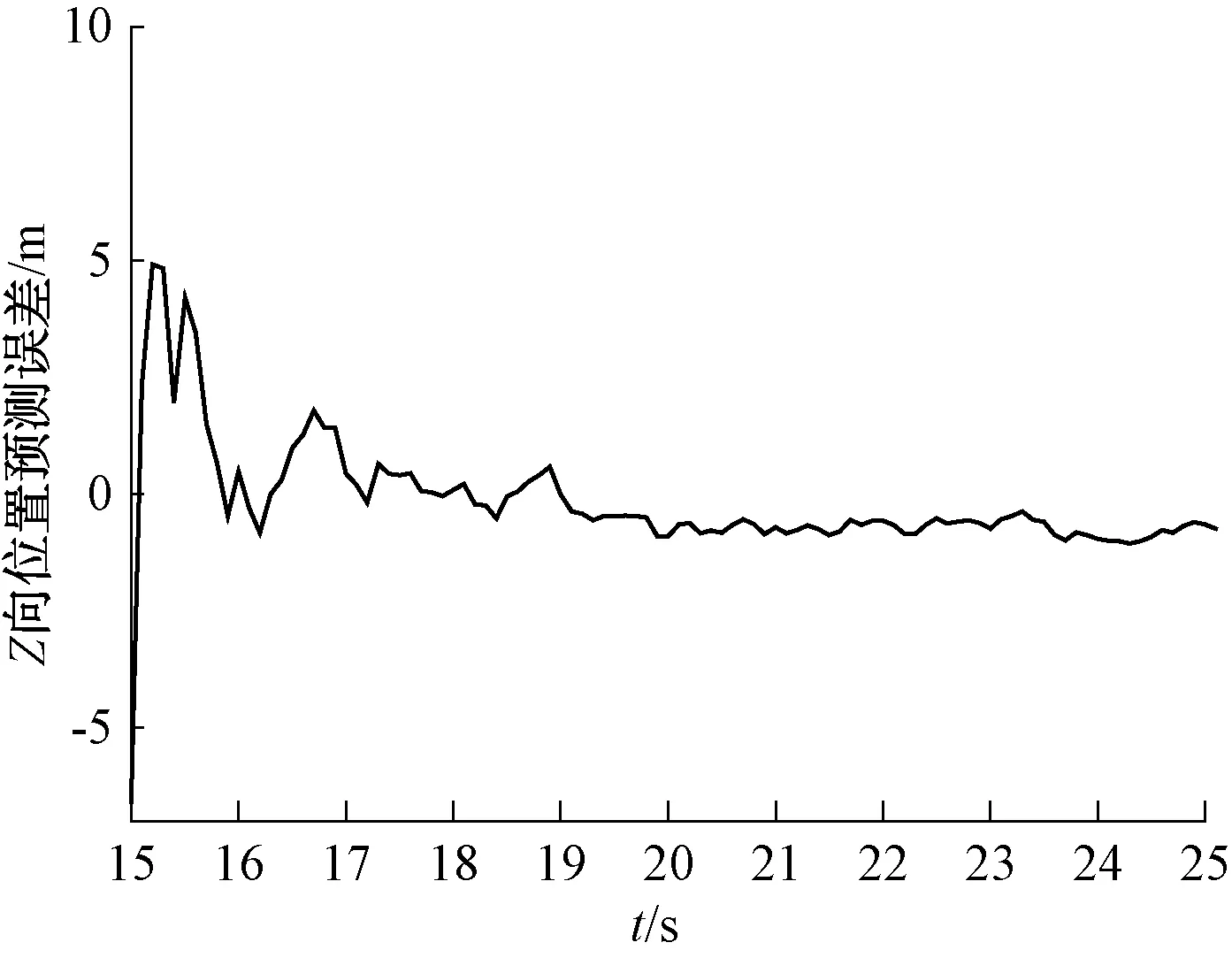
图4 Z向位置估计误差
由图2~图4可以看出,估计误差基本在3 s内完成了收敛,说明基于扩展卡尔曼滤波的有控弹道滤波精度高、收敛快,适用于弹道参数估计。据此可选取滤波时间长度为3 s,进行落点预测及控制指令解算。对1条有噪声的弹道进行滤波估计,结果如表2所示。

表2 噪声与滤波结果对比
从表2可以看出,速度估计误差大部分可以保持在0.2 m/s以内,位置估计误差基本保持在3 m以内,说明基于有控弹道模型的扩展卡尔曼滤波估计精度高,适用于二维弹道修正弹飞行过程中的参数估计。
3.2 制导控制仿真验证
在40°射角,从弹丸出炮口15 s开始修正,每隔5 s进行1次落点预测,按照表1误差条件进行仿真,以目标点坐标为(22 950,600)m为例,某条件下无控落点实际坐标为(23 099,671)m,其射程方向与目标点相比偏差远149 m,侧偏方向偏左71 m。对于该算例,制导系统在15 s开始起控,每隔3 s解算1次落点并计算滚转角指令,将弹药不断向目标点引导。图5~图6分别为该过程中预测落点及控制指令的变化曲线。从图5可以看出,落点的射程偏差从149 m缩减至14 m,侧偏从71 m缩减至2 m,表明本文制导算法具有良好的制导精度。
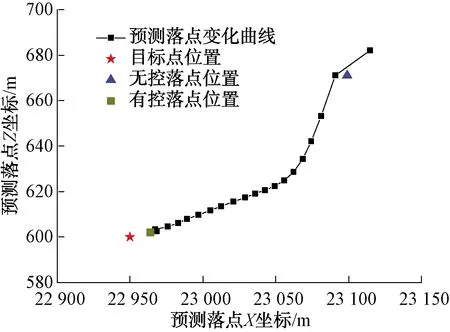
图5 预测落点坐标变化曲线
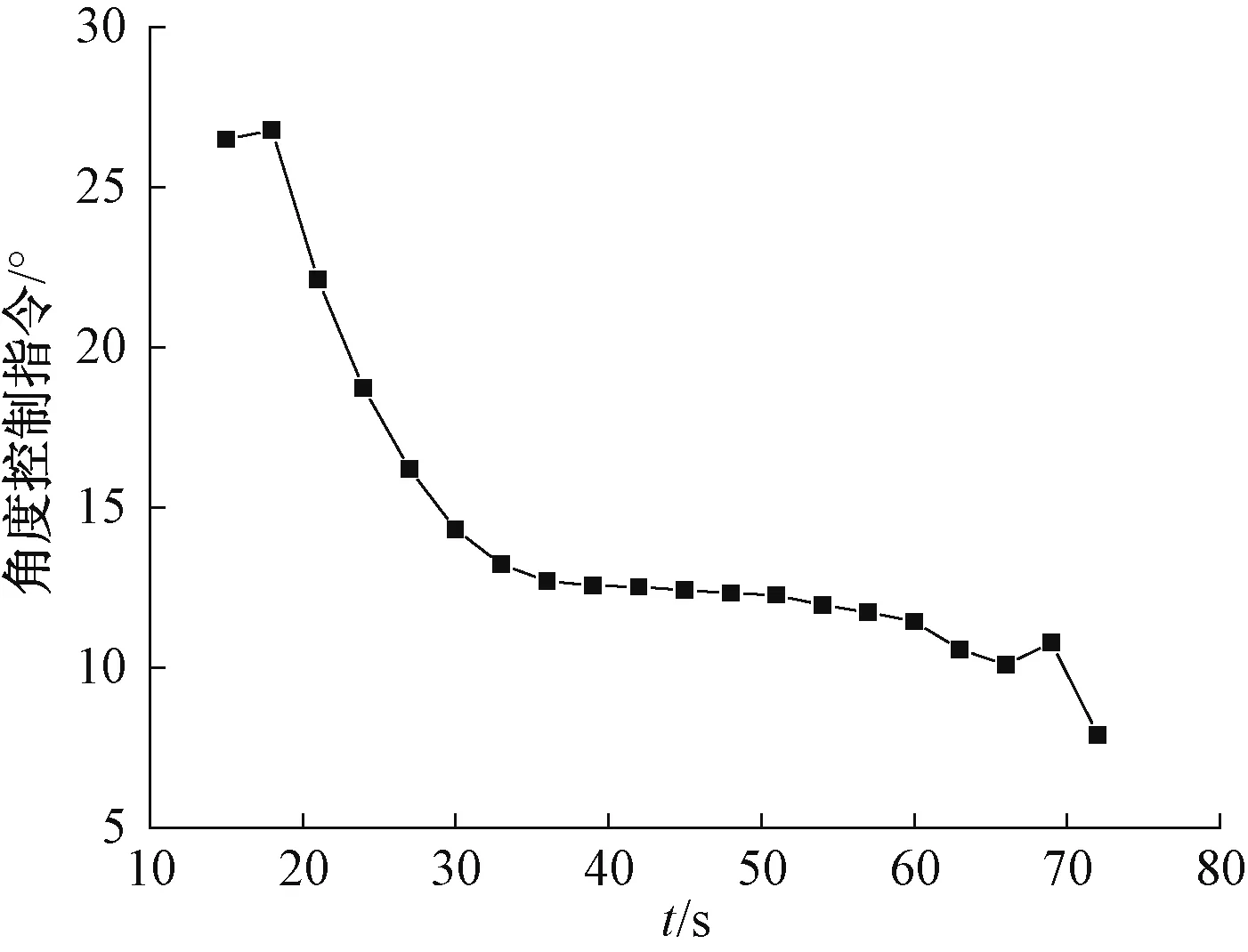
图6 控制指令变化曲线
为了进一步验证制导控制系统的导引精度,采用了蒙特卡洛打靶方法,在射角40°、目标点位于(22 950,600)m情况下进行仿真,结果如图7所示。仿真结果表明,通过二维弹道修正,可以显著降低无控弹药落点的散布范围,并可以将大部分弹药修正至目标点附近位置。在40°射角情况下,圆概率误差(CEP)约为28 m。
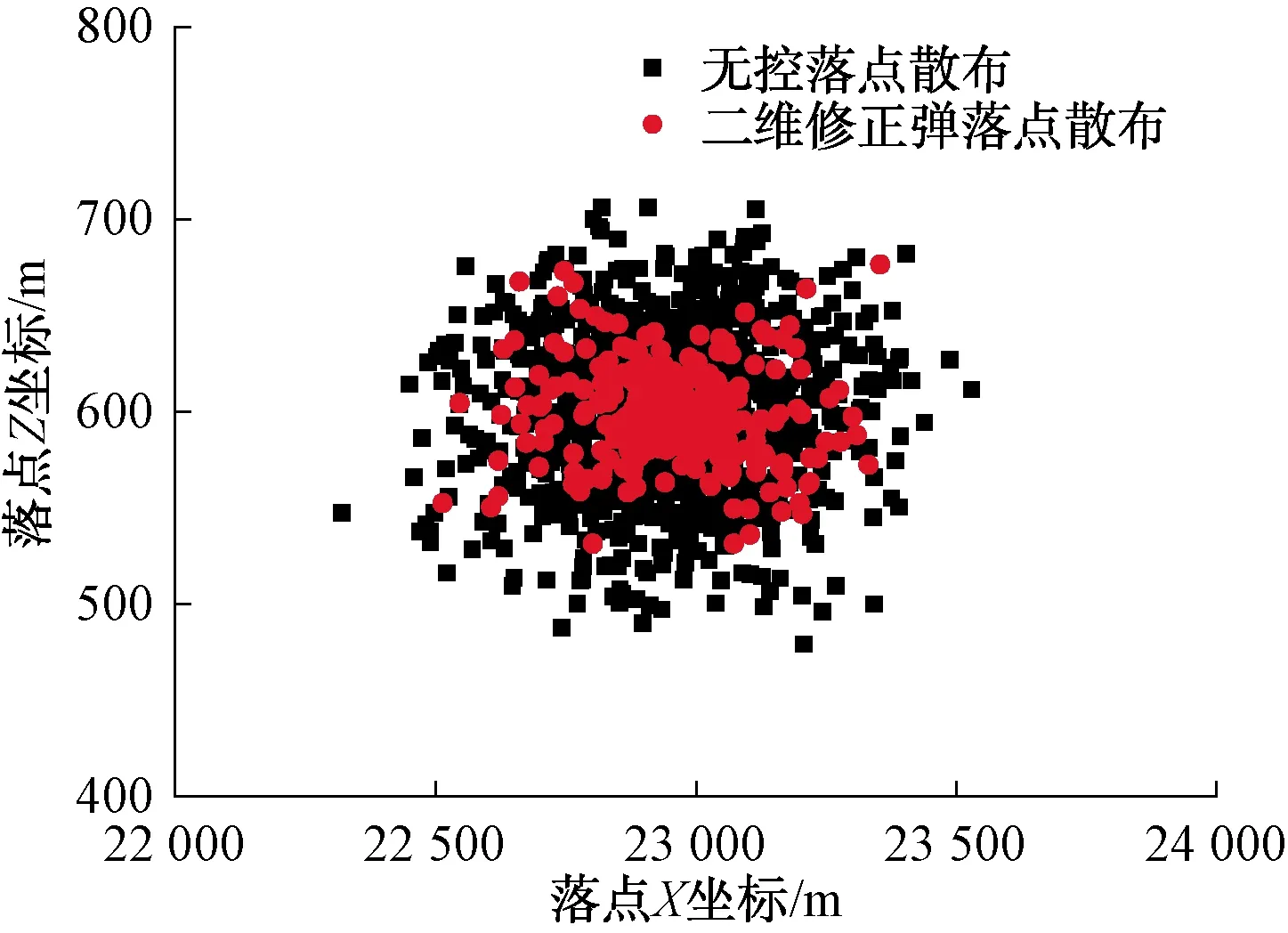
图7 48°射角条件下二维修正弹落点散布图
4 结束语
本文提出了一种基于扩展卡尔曼滤波的有控弹道滤波估计及制导控制指令解算方法。与传统的无控弹道滤波算法相比,在滤波状态模型中引入了控制量,通过对有控弹道进行滤波,获取弹药的状态估计值。仿真结果表明,该方法有效地减小了卫导测量精度引起的误差,提高了落点预测精度,通过闭环制导控制,可以显著降低落点散布范围,提高弹药的落点密集度。
