基于压缩感知的MIMO-OFDM无线通信信道估计技术研究

赵鼎臣

（中国电子科技集团公司第二十八研究所，江苏 南京 210000）

0 引 言

当前，随着科技的进步，移动通信技术已经发展到了第四代（4G），并逐渐朝着第五代通信技术演化[1,2]。4G通信核心技术为正交频分复用（Orthogonal Frequency-Division Multiplexing，OFDM）技术和多输入多输出（Multiple-Input Multiple-Output，MIMO）技术。OFDM技术是将信号调制到不同子载波同时输出，传输效率提升的同时能够有效抵御干扰。MIMO技术可以利用多天线信道和空时编码技术大幅度提高数据传输的速度。将MIMO技术和OFDM技术相结合，构建出MIMO-OFDM系统，不仅可以发挥二者在传输上的优势，而且可以克服码间串扰和信道间干扰，是5G通信的关键技术之一。

信道估计历来是通信系统中实现信息精确解调的关键技术。传统信道估计主要依托最小二乘技术实现，这种方式须放置大量的导频信号而导致频带资源被消耗。压缩感知技术作为打破奈奎斯特采样定理的新型采样技术，引入到信道估计中可显著降低导频信号的数目，从而提升频带资源效率。对此本文开展基于压缩感知技术的信道估计技术研究工作，旨在推动通信系统的完善设计。

1 OFDM通信系统传输模型

OFDM信道传输模型如图1所示，根据OFDM信道传输模型来对OFDM信道做如下解释。目标数据由随机方式生成，基带信号中存在丰富的低频分量，在大多数通信传输系统中传输时，可以通过相应的调制技术来提升传输性能，如采用16PSK和16QAM等[3,4]。根据当前应用情况，16QAM相对性能较佳，因此本篇文章中使用16QAM调制方式来进行实验设计。

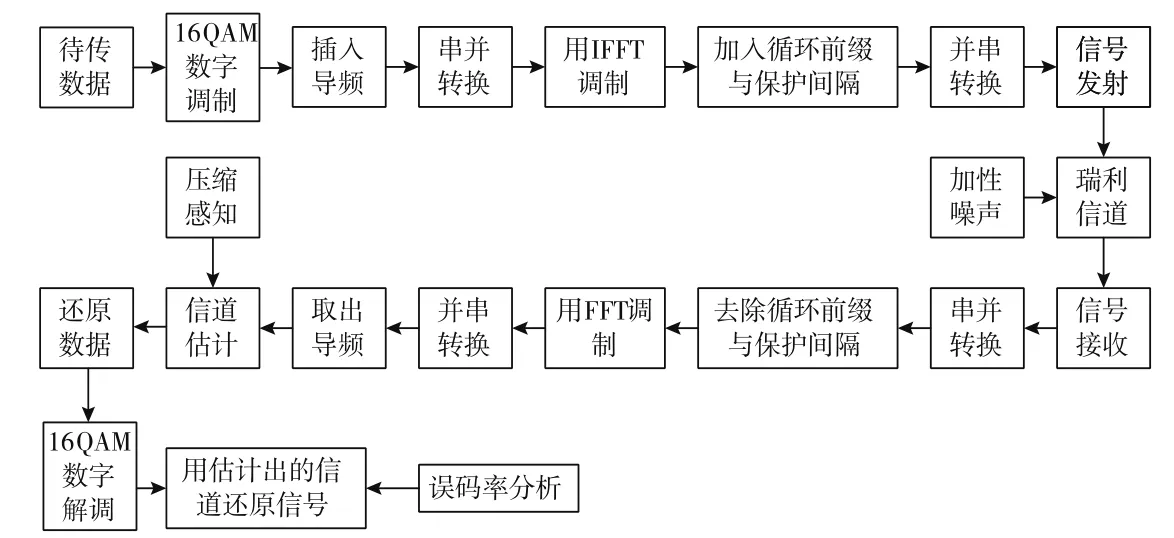
图1 OFDM信道传输模型

为了进行信道估计，本文在发送端插入导频。调制串并转换后的数据，OFDM技术的调制方式与IFFT变换非常相似，因此采用IFFT变换对OFDM发送符号进行调制。此外，在通信系统中，传输信道通常存在子载波间干扰和符号间干扰现象，所以在进行OFDM调制时需要加入保护间隔和循环前缀，接下来进行并串转换再发送至多径瑞利衰落信道，并考虑噪声进行传输。

信号发送后，接收端对获取的信号进行串并转换处理，并去除循环前缀和保护间隔，采用FFT方法进行解调，以获取传输信号，然后从传输信号中提取设定的导频。由于导频是自己加入的，发送前的导频和发送后的导频都已知，因此在接收端导频附加上了信道的特征，通过对发送和接收的导频做相应的运算就可以将信道估计出来，再用估计出来的信道对接收到的信号进行还原和数字解调，最终得到有用数据。

2 基于Denoiser-ISTA的OFDM信道估计原理

2.1 ISTA算法原理

压缩感知技术的关键在于压缩信号的重构，重构过程实际上可以理解为对线性逆问题的求解。ISTA算法是其中的典型方法，该方法对应的求解问题模型可表述为：

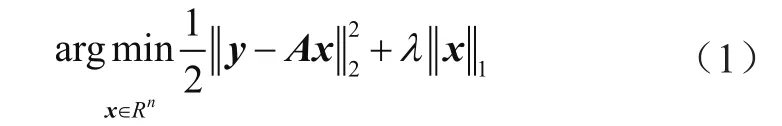
式（1）为典型的L1正则化模型，其中λ为正则化参数；A表示观测矩阵；x、y分别为输入信号和测量信号。上述优化目标函数由保真项||y-Ax||22和正则项||x||1组成，其中保真项||y-Ax||22的意义在于获得最真实的信息，其构造形如最小二乘形式。正则项||x||1是获取真实信息x的最稀疏表示，即保证真实信息x的稀疏性，以此作为先验条件。在该先验条件下，正则项可对信号分量进行有效识别。因为在较宽的信号变换域空间中，如傅里叶空间和小波空间等信号分量分布更加集中，其对应的幅度较大，而噪声对应的幅度由于泛化的原因而呈现出较小的幅值，由此通过一定的筛选可有效实现信号和噪声的有效分离，但是也有可能将幅度较小的信号分量筛选出去。基于此将二者联合起来，采用制衡的方式实现二者之间的平衡而获得相应的优化结果。

针对这一函数，根据Majorization-Minimization优化框架，可得对应优化步骤如下。

首先，求解保真项梯度，并进一步梯度迭代，其计算如下：

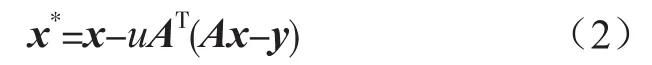
其次，利用导数为零即为极值点的思路求解如下L1正则化模型：

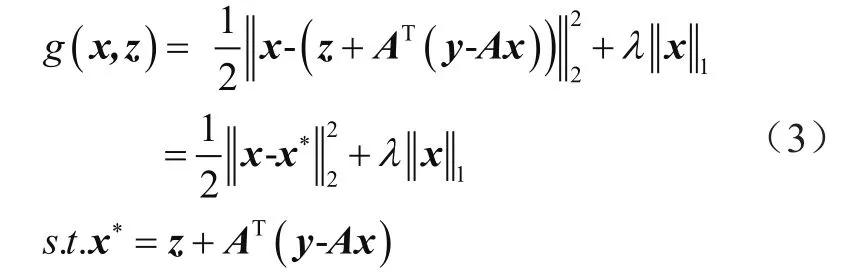
最后，判断所迭代求解的结果是否满足迭代要求，满足条件输出，不满足条件则重复上述两步。

2.2 Denoiser-ISTA算法基本理论

根据上述分析可知，ISTA算法对应的优化模型可重写为：

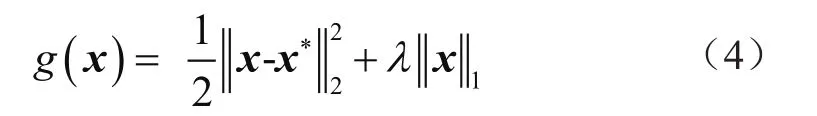
式（4）为ISTA算法核心部分，鉴于该环节对应的去噪性质，本文将该项表述为滤波形式，即通过滤波器对应的滤波效果实现对信号叠加噪声的去除。对应的表达为：

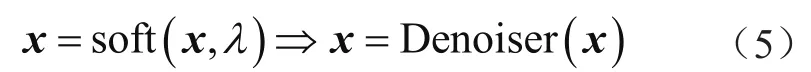
通过上述的过程来实现对本文算法的重新构建。输入测量值y、测量矩阵A、正则化参数λ以及优化尺度u，输出重建原始信号x^，初始化重建原始信号x=0。首先求解保真项梯度，并进一步梯度迭代，计算为：

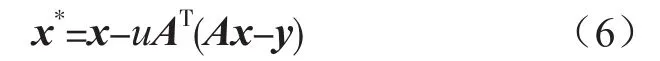
其次Wiener滤波器替代阈值收缩迭代环节，采用公式（5）结论形式进行求解。最后判断所迭代求解的结果是否满足迭代要求，满足条件输出，不满足条件则重复上述过程，直至满足条件后输出。

2.3 基于Denoiser-ISTA的MIMO-OFDM信道估计方案

2.3.1 信道估计模型构建

假设发射天线的数量为M，包含K的下行MIMO-OFDM系统信道估计的大规模单接收天线用户单元中估计一个OFDM符号采用的载波数量是N，循环前缀的长度为NCP[5]。接收单元对应信号模型可进行数学表达为：

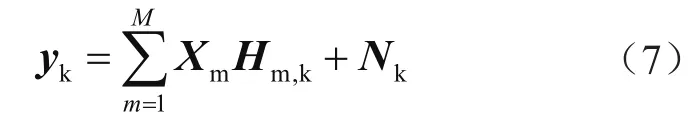
式中，yk表示第k个用户接收到的OFDM符号中对应的N×1的信息；Xm为对角矩阵，即第m根发送天线发送的N×N维度信号，而对角阵的正对角线的元素都是对应天线发送的N×1信号序列；Hm,k表示第m根发送天线与第k个用户之间的N×1频域系统中的信道参量；Nk表示为高斯白噪声[6]。

由此可得频域信道和时域信道之间的数学关系为：

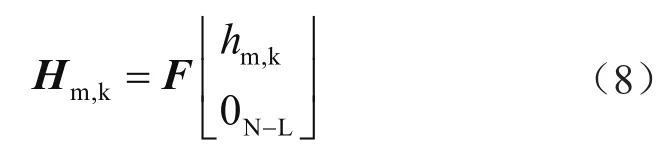
式中，F表示离散傅里叶变换矩阵，而其对应的第（k,l）个元素对应的值为：

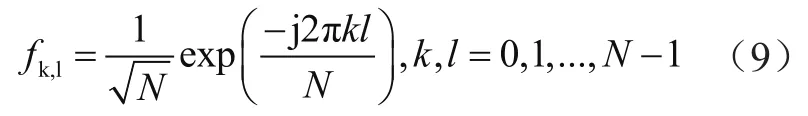
hm,k描述为相对应的时域信号。在现实的通信中，由于传输路径中存在阻碍而导致多径信号再不同时间下到达接收端，由此得到延时误差。该误差的存在促使传输信道呈现延时域的稀疏性，因此可采用压缩感知可实现精确的信道估计过程[7]。该处信道信息在时延域上的数学关系为：

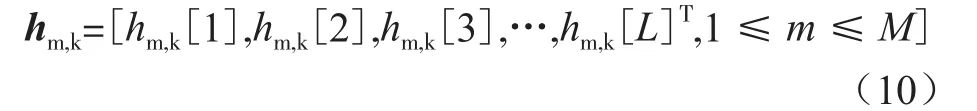
式中，L代表时延域的等效信道长度。

2.3.2 导频设计

对于导频的放置是一个科学问题，导频放置图案需要在一些准则的规定下进行设计。在压缩感知框架下导频阵列实际上为观测矩阵，因此需要满足RIP准则和最小相关性准则[8,9]。对于这一类问题，一般采用随机导频即可满足。为了降低本研究的整体复杂性，本文的设计中采用随机放置的方式来安置导频，从而以优化设计局面。

2.3.3 时延信道估计

上述分析可知，MIMO-OFDM系统信道具有稀疏性[10]。估计过程中一组天线在一个OFDM载波中选择Np个载波作为导频子载波，因此共有Np×Q个导频子载波。在接收端用户接收到的单个OFDM符号上第q组天线的导频信号yq,k=CNp×L可描述为：

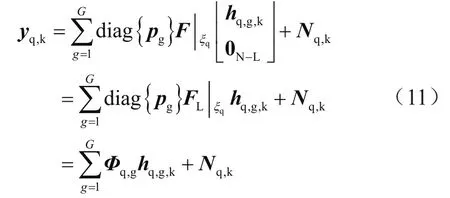
式中，{pg}为导频子载波上的导频序列；hq,g,k表示时延域信道冲击响应；ξq表示第q组天线在OFDM信号中导频子载波的索引集合Φq,g为天线g发送的导频序列，接收到的全部天线导频信号表示为：

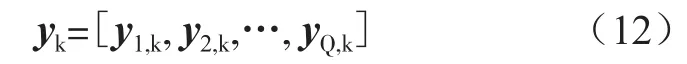
对此可以通过对该公式来求解获取稀疏特性的时延域信道。

2.4 方案实现

图2中展示整体实现方案，即获取相应的导频x及导频对信道的响应y，此时的y被叠加上噪声，然后进行稀疏重构，为了使重构过程更加精确，需要在MIMO-OFDM信道系统中引入基于Denoiser-ISTA算法进行信道估计，从而以提升整体的信道估计效果。

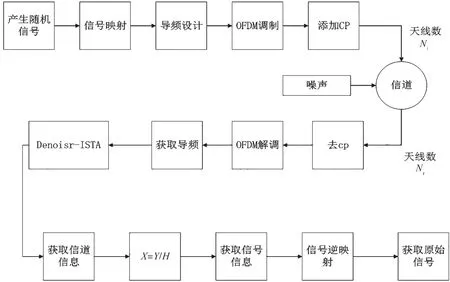
图2 系统方案实现框图

根据实验结果可知，相同噪声下，本文算法的整体估计性能相比其他对比算法具有显著的优势。导频数目的增加，对应的信道估计精度也会提升。可知在一定的估计精度条件下，LS算法要想实现本文算法的效果显然需要更多的导频，由此可知本文提出的算法及其信道估计方案能够在一定精度条件下，实现信道估计使用的导频数目的削减，从而能够提升信号传输效率，并同时降低导频污染风险。

3 结 论

本文提出的Denoiser-ISTA算法及其对应的信道估计方案在噪声压制和减少导频等相关方面具有较大优势。此外本文所构建是基于L1正则化模型下的优化算法，其最大的优点在于不需要信道稀疏度作为先验信息，这相比于OMP等一系列算法具有更为广泛的实用性。总之，本文所提出算法具备的这些优势对于推动基于CS理论的大规模MIMO-OFDM信道估计技术发展有着关键支持。