含分布式电源配电网络重构遗传算法优化研究
2020-04-26贾文宇
贾文宇
(华北水利水电大学,河南 郑州 450045)
0 引 言
配电网重构是一种基于系统运行状态,经优化网络拓扑来提高网架运行效率与电能质量的举措。现阶段,学者在研究配电网优化问题上大多采用数学优化理论算法[1]。其中GA具有简单、便捷、收敛性佳以及全局搜索能力强等优点而被广泛应用于配电网重构问题的求解中[2]。但是常规的GA无法针对配电网的结构特性进行编码和遗传操作,这在一定程度上会产生大量不可行解,进而弱化搜索效率。此次研究针对上述问题提出一种应用于含分布式电源配电网重构的GA优化方式,在优化GA编码方式的基础上,将机会约束检验融入到生成种群和交叉变异等流程中,以此求解含不确定性的配电网重构问题,进而为运行工作者的调度决策提供借鉴。
1 含不确定性的配电网重构模型
1.1 最大供电能力的机会约束模型
配电网最大供电能力指标即配网在达到节点电势差约束与支路容量约束条件下所输出的最大负荷[3]。目标函数如下:

式中,N代表节点个数;Pi代表各节点最大负荷;Pint.i代表节点i的同步负荷;Pd.i代表节点i的负荷增长基数;k为负荷增长系数。为了客观的对比优化结果,将最大供电能力等效为最大供电倍数K,进一步定义K=1+k[4]。
供电能力计算的约束条件如下:

式中,Uimin、Ui以及Uimax分别代表节点i的电势差、下限以及上限;I1和I1max分别代表l流过的电流及其上限;f(Ps)和f(Pw)分别代表光伏和风电的出力概率密度函数;Ps、Psmax、Pw以及Pwmax分别为抽样得到的光伏、风电输出功率及上限[5]。
此次研究采用重复潮流法计算供电能力,在潮流计算的过程中,将分布式电源等效为PQ节点,在此基础上经正态分布体现节点负荷的不确定性。含分布式电源与负荷等不确定因素,所得供电能力机会约束模型为:

式中,Pr即分布式电源等效特定节点负荷;K为不确定信息下的最大供电倍数;Kmargin表示供电能力安全阈值;α为预设供电能力机会约束置信水平。
1.2 含供电能力和分布式电源出力机会约束的配电网重构模型
将统计模拟得到的最大供电倍数K基于降序进行排列,依附于预设的置信水平可以获得供电能力安全阈值Kmargin,以此数值最优为重构目标,构建的目标函数为 max。
在重构的过程中,一定要达到下述约束条件:
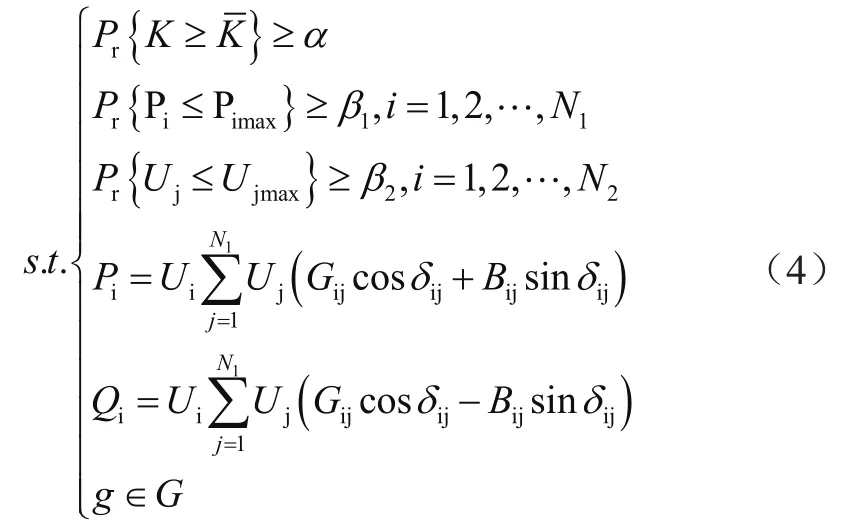
式中,Pr为支路供电能力安全阈值;Pi和Uj分别表示不确定状态下支路i的功率和节点j的电势差;Pimax和Ujmax分别表示支路i允许功率极值与节点j允许电势差极值;α、β1以及β2分别表示供电能力、支路容量以及节点电势差的置信水平;N1和N2分别表示网架支路和节点总量;g即各重构完成的配电网架结构;Qi为各网架支路节点功率;G为各辐射状连通网架集合。
2 GA优化及其应用流程
因为配电网具有闭环设计和开环运行的特性,所以在重构时要从根本上确保所有个体的辐射和连通性。因此,在应用于配电网重构领域时要对GA实施进行下述优化[6]。
2.1 初始种群生成策略
针对常规问题,一般的编码方法大多是通过二进制数对全部开关进行编码,也就是通过0和1去体现联络开关和分段开关的开合状态,此方案的特点是编码便捷和容易操作[7,8]。不过此方法并未考虑配电网的运行特点,会造成算法运行时产生大量不可行解,更有甚者会直接影响计算效率[9]。此次研究的编码方法中,针对某个含b个节点和l条支路的配电网架,将组成符合网络拓扑约束网架的各支路编号整合到集合N1,将其他支路编号整合到集合N2,连结N1和N2即可形成新个体。经这种将网架树枝和连枝分别编码的方法,能够确保初始种群内的所有个体都具备辐射性与连通性,因此确保算法求解的可行性要求。生成流程如下:
(1)设置N为所有备选线路集合,N1和N2即空集合,D表示网架变压器所在节点集合;
(2)从N中找出全部带有D中节点的支路,在此基础上随机抽取一条作为新增线路;
(3)将流程(2)抽取的支路整合到N1之中,如果N1线路组成的网架无法达到辐射性要求,那么将此支路整合到N2,反之将此支路的末节点加入D;
(4)重复流程(2)和(3),在N线路已全部加入N1和N2后停止,对新个体实施各项机会约束检验,如果达到标准即可加入初始种群,反之回到流程(1);
(5)在初始种群中个体数量达到预设值的情况下算法结束。
2.2 交叉操作流程
为了从根本上确保初始种群中的个体在交叉操作后仍达到拓扑约束要求,对交叉操作算法实施下述优化。(1)从初始种群内以轮盘赌形式选择两条染色体作为父、母代;(2)在特定长度区间中随机选择一个染色体交叉点,将处于父代交叉点前的全部支路编号加入子代染色体的集合N1;(3)删除母代染色体内所有和子代染色体相同的支路编号;(4)将母代染色体内其它支路编号逐一整合到子代染色体,每次整合都要对“环”进行检查,如果达到辐射性要求即可加入集合N1,反之加入N2;(5)对构造的子代染色体实施各项机会约束检验,如果达到约束要求,则交叉操作完成,反之回到流程(1)。在进行交叉算法时,首先选取父代部分辐射状支路加入到子代染色体,在此基础上从母代内选取不重复的支路逐一加入到子代染色体。通过上述方式所形成的子代个体内包含了父母代的信息,而且拓扑结构达到连通辐射性要求。
2.3 随机机会约束检验方法
在进行遗传操作时,要对算法中的个体实施电势差、功率以及供电能力机会约束检验[10]。此次研究采用统计模拟检验机会约束条件,流程如下。(1)已明确置信水平α,对于初始种群和重构时所生成的某个个体,设ξ=(ξ1,ξ2,ξ3,…ξn)为n维的随机向量,ξ1,ξ2,ξ3,…ξn分别表示分布式电源和各节点负荷所满足的概率分布;(2)从n维随机向量ξ内随机生成一组抽样值θ1,θ2,θ3,…θn,也就是分布式电源出力和各节点负荷的一组单次计算抽样值;(3)对此时的个体实施确定性潮流计算,进一步检查电势差、功率有无越限,通过重复潮流法计算此状态下最大供电能力倍数K,如果K≥Kmargin,同时各节点电势差和支路功率不越限,即可明确事件成立;(4)拟定试验次数为S,S′即所有试验次数中事件成立的次数,如果S′/S>α,即可认为达到置信水平α,随机机会约束条件成立,此个体为可行解。
2.4 算法流程
GA优化整体流程如下。(1)选择GA初始参数,其中包括种群大小以及变异概率等;(2)生成满足连通辐射性的网架加入种群;(3)依附于光伏电池、风机以及负荷的概率密度函数实施统计模拟,在此基础上对种群中染色体进行机会约束检验,如果未达到标准则重新生成并替换;(4)将统计模拟得到的供电能力结果根据降序进行排列,依附于置信水平获取染色体适应值;(5)通过轮盘赌的方式选择两条父代染色体,对父代染色体实施交叉操作生成一条子代染色体,此染色体同样达到拓扑约束要求,在此基础上依附于设定的变异概率对此染色体实施变异操作;(6)和流程(3)相似,对子代实施机会约束检验,同时计算子代适应系数,如果没有达到机会约束或适应系数较之原种群没有提高,则返回流程(5);反之将子代加入种群替换适应系数较低的染色体;(7)在种群中全部染色体都相同的情况下,即可证实算法已收敛。
3 算例分析
笔者通过IEEE-33节点配电网系统进行验证。IEEE-33节点网架拓扑结构见图1。初始网架的整体负荷为3 715 kW+j2 300 kvar。在节点8与24分别接入光伏发电系统与风力发电系统,风机切入风速为4 m/s,额定风速为12 m/s,切出风速为25 m/s,额定功率为400 kW。光伏系统整体面积为10 000 m2,光电转换效率为0.14。
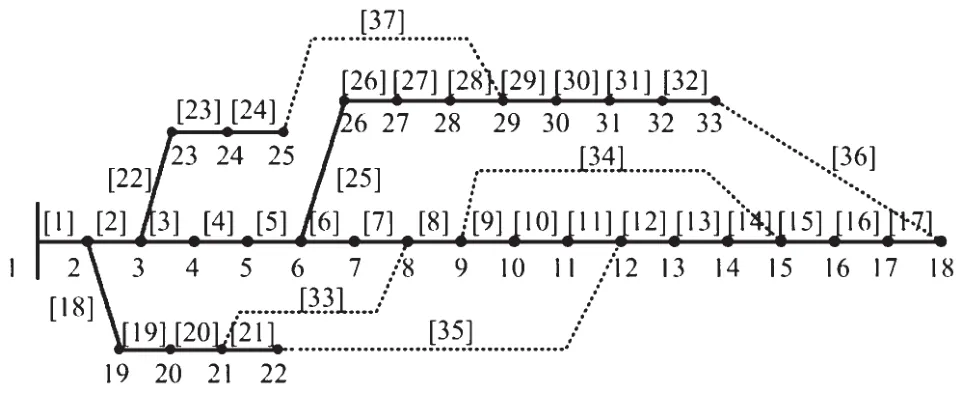
图1 初始网架拓扑
3.1 含分布式电源的配电网重构结果分析
在通过GA求解模型的情况下,初始种群大小拟定为20,变异率拟定为0.1,统计模拟次数N为5 000。取各约束条件的置信水平为0.8,设置不同的分布式电源,得到的重构结果如表1所示。

表1 网络重构结果
通过表1能够得到以下结论。在重构方案中,无分布式电源方案供电能力增加6.05%,而接入光伏系统和风机的方案供电能力分别增加7.25%与5.15%,由此可证,在重构的过程中加入供电能力机会约束能够在一定程度上深化配电网供电能力,同时接入分布式电源对供电能力的改善更为显著。在不同类型分布式电源同时接入配电网的情况下,供电能力达到最优,由此可证,采用此次研究所提出的重构方法对含多种分布式电源的配电网实施重构,能够在一定程度上增加网络的供电裕度,同时可以加强配电网的利用率以及安全性。
3.2 置信水平对优化方案影响分析
在光伏系统和风机同时接入的情况下,分别取不同的置信水平对模型实施求解,重构结果如表2所示,其中置信水平为0.8状态下的收敛曲线如图2所示。

表2 网络重构结果

图2 置信水平为0.8的收敛曲线
通过表2的重构结果,得到以下结论。(1)在配电网同步接入多种分布式电源的情况下,重构结果的供电能力会随着约束条件置信水平的提高而降低,由此印证对机会约束要求越高,方案的供电能力就越低。(2)低置信水平下的重构结果尽管具有较高的供电能力,但无法体现全局状态,且出现极端状况的概率较高,实际应用性偏低。而提高置信水平导致供电能力降低,对重构结果的安全性会产生影响,所以置信水平不宜过高。(3)总的来说,在多种分布式电源同步运行的状态下,可选择置信水平0.8作为参考数值,此时重构结果兼顾了置信水平和供电能力的要求,具有较强的适用性。
4 结 论
此次研究融合了机会约束理论,构建含供电能力机会约束的配电网重构模型,分析了配电网负荷和分布式电源出力的不确定性,从根本上避免了确定性负荷下重构结果过于保守的问题,优化方案更为丰富,且具有更高的适应性。此外,此次研究GA优化可以依附于配电网运行特性,规避不可行解,深化算法效率,在此基础上明确负荷和分布式电源出力的随机性,加强了方案对不确定性的适应度。算例结果表明此次优化算法的有效性,进一步印证了它适用于不确定性配电网重构问题。算例结果显示,经笔者所提方法实施重构,能够从根本上加强配电网供电能力。在配电网同步接入多种分布式电源的情况下,置信水平越高,优化方案的供电能力就会随之降低,所以要依附于实际运行需求进行有针对性的设定与调整。
