块稀疏广义正交匹配追踪算法*
2020-04-25杨恩蘋王彦帅隋天宇
杨恩蘋,周 三,王彦帅,隋天宇
(中国电子科技集团公司第三十研究所,四川 成都 610041)
0 引 言
压缩感知作为一种可以突破Shannon-Nyquist定理局限的采样理论,近十年来受到了广泛的关注,在通信、遥感、遥测、医疗图像等领域得到了广泛的应用。对于稀疏信号或可被稀疏分解的信号,压缩感知能够以远低于信号Nyquist 速率的采样率完成采样,其理论基础如下,

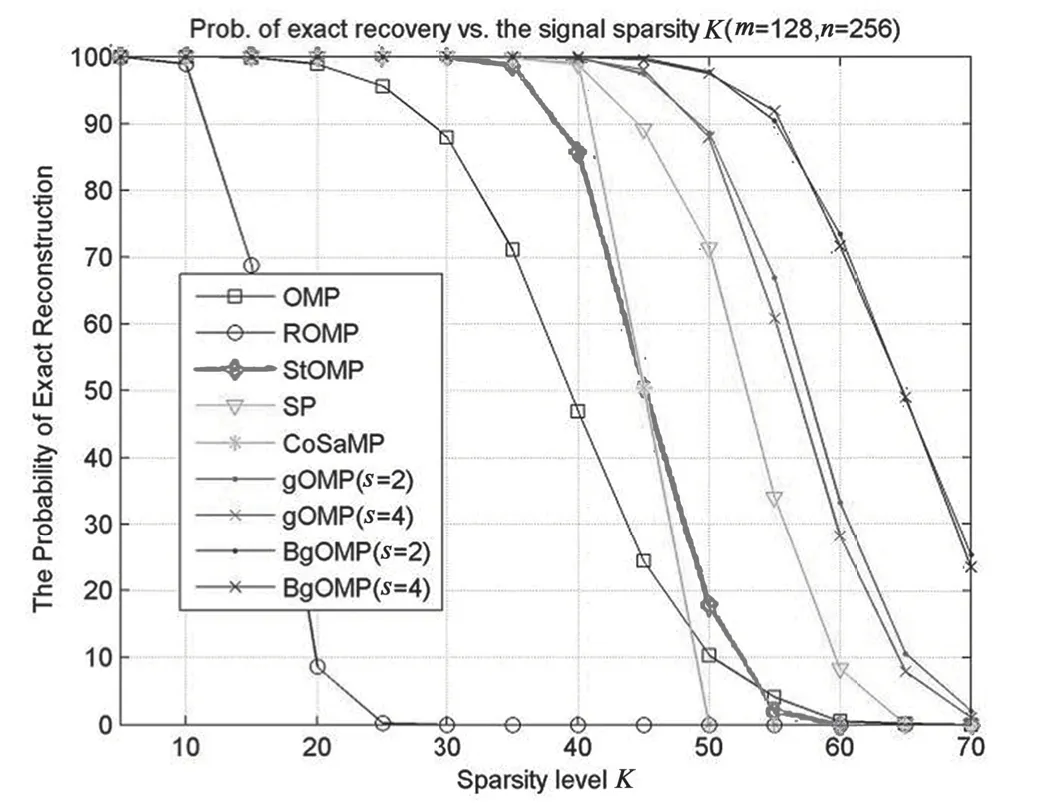
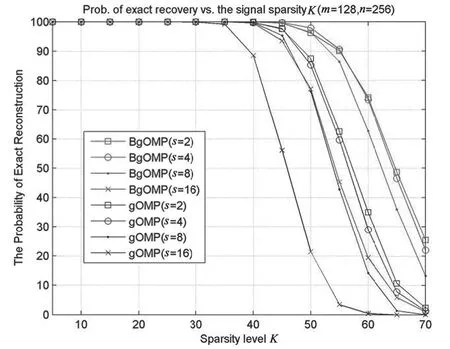
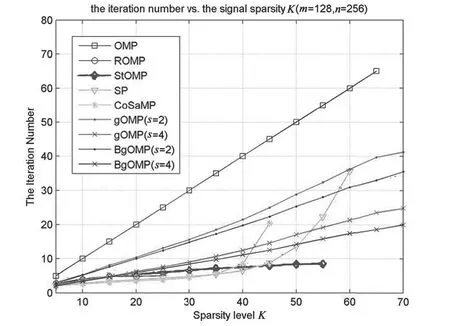
其中,x 是长度为n 的稀疏(或可稀疏分解)信号,Φ 是维度为m×n(m< 不难发现,在m< 一般说来,上述算法适用于重构非零元完全随机分布的稀疏信号。然而,一些研究发现在某些稀疏基的约束下,例如傅里叶基和小波基等,块稀疏信号更加符合人造信号的特点[6-9]。此类信号的非零元呈“块状”随机分布,而非单个非零元随机分布。文献[10]提出了针对一种特殊块稀疏信号的重构方法,但要求所有非零块的长度相等,零块的长度为非零块的整数倍。文献[11]提出的算法,不要求非零块长度相等,但是需要利用信号中关于块结构的先验知识,即知道信号中每个块的长度,只是不知道某个具体的块是全零块还是非零块。 综上,现有块稀疏信号重构算法仍存在局限,有进一步提升的空间。因此,本文针对块稀疏信号重构问题,基于计算量较小的且性能优异的gOMP,提出了适用于块稀疏信号的BgOMP 算法,给出了算法的详细介绍,证明了算法的无失真重构的充分条件,并通过仿真证实了算法的有效性与优越性。 设信号总长为n,信号中非零元素的个数为K,若K< 其中,ψ 是维度为n 的稀疏分解基(若信号无需稀疏分解,则表示单位矩阵),θ 为非零块的系数,I 是包含所有非零块的索引值的集合,集合I 的势为|I|=||I||0=K。 为方便理解,这里通过图示的方式说明块稀疏信号特点。图1 表示一个信号向量,每个方块表示一个元素,白色方块表示0 元素,着色方块表示非零元素。可以看出,该信号包含3 个非零块,稀疏度K 等于9,集合I={3,4,5,7,8,10,11,12,13}。 图1 块稀疏信号示意 所有的匹配追踪算法都具有相通的基础原理:计算y 与Φ 的相关值,通过相关值的大小估计出x的非零元。不同的匹配追踪算法的区别主要体现在潜在非零元的选取方法,以及最终确定潜在非零元的方法上。本文提出的BgOMP 与gOMP 的主要区别在于,利用了块稀疏信号的稀疏特性——非零元在信号向量中分段连续[9]。换句话说,如果通过相关计算找到了一个正确的潜在非零元,那么索引值与该非零元相邻的元素(如果存在的话),必然也为非零。例如,若通过相关运算,估计出图1 中索引值为10 的元素非零,那么索引值与10 相邻的9和11 中,至少有一个为非零元素。算法伪代码如下: 表1 BgOMP 伪代码 算法所需的输入值有传感矩阵、采样值、稀疏度与算法的估计步长。前三项输入是大多数匹配追踪算法的必备输入,当然目前也存在一些能够估计信号稀疏度的算法,但通常计算复杂度较高。算法的估计步长是指每次迭代时,通过相关运算选取的非零元个数。 算法需对迭代次数、集合I、残差r、块的选取范围进行初始化。在初始状态下,显然有,迭代次数为0,集合I 为空集,残差r 等于采样值。需要说明的是块的选取范围,通常压缩感知要求信号的稀疏度不超过m/2,否则任何重构算法都无法重构信号,因此,在这个极限范围内,利用块稀疏信号特性选取潜在的非零元素。 算法更新迭代次数后,首先计算矩阵Φ 与残差r 的相关值,并构建两个集合,第一个集合Λ 包含最大s 个相关值对应的索引值,第二个集合包含最大m/2 个相关值对应的索引值(仅需一次相关计算,伪代码中两项相关计算是为了区分两个集合)。然后,寻找Λ 中所有元素的相邻元素,若这些相邻元素同时也属于第二个集合,那么判定为有效。最后,将上次迭代产生的估计集合与本次迭代找到的最大值集合,以及这些最大值的有效相邻元素集合这三个集合合并,进而计算残差,更新残差并进入下一次迭代。 众所周知,迭代算法必须设置停止条件,在本算法中停止条件与gOMP 完全相同,停止条件1 可以设置为一个极小的固定常数,当残差大于该常数时,将进行下一次迭代;停止条件2 为迭代次数,因知晓信号稀疏度,且估计的信号支撑集不应超过m,所以,若迭代次数大于稀疏度或m/s,需要停止迭代。 与众多压缩感知重构算法类似,本文仍然使用受限等距特性(RIP)对算法进行约束。首先说明RIP 的定义, 定义1[12]:若对于任意的K 稀疏向量x,矩阵Φ 以常数δ(0<δ<1)满足 那么称Φ 满足K 阶RIP。 下面,利用gOMP 的相关结论证明BgOMP 的有效性。 引理1[4]:假设nx∈R 是一个K 稀疏的信号,N为gOMP 的估计步长,只要其RIP 常数满足 那么gOMP 在第一次迭代时,必然能够找到至少一个非零元的正确位置。 定理1:假设nx∈R 是一个总稀疏度为K 的块稀疏信号(K ≥2),s 为BgOMP 的估计步长,只要其RIP 常数满足 那么BgOMP 在第一次迭代时,必然能够找到一个非零块的正确位置。 实际上,在定理1 中,步长s 等效于gOMP 的步长N,区别在于第一次迭代,完成相关计算后,BgOMP 将选择相邻元素,加入估计的支持集。下面证明选择相邻元素,不会消除已有的正确元素。 证明:由引理1 可知,当成立时,有: Λ1中的所有s 个元素,从数值上来看,可能完全不相邻,也可能是连续的s 个数字,因此, 可得: 可知只要在第一次相关计算时,能够找到至少一个正确的非零元,这些正确的原始必然被保留在估计支撑集中。 类似地,可以利用gOMP 后续迭代的约束条件给出BgOMP 的约束条件。 引理2[4]:设N ≤min{K,m/K}且gOMP 进行了l次有效的迭代,那么当满足以下条件时,第l+1 次迭代必然成功, 定理2:设s ≤min{K,m/K},那么当满足以下条件时,BgOMP 必然能够重构原始信号: 证明:由引理2,并结合增加向量元素后集合势的大小,可知,当BgOMP 进行了l 次有效的迭代,那么当满足时,第l+1 次迭代必然成功。同时,考虑到: 因此,BgOMP 满足即可保证信号重构。 此外,从可以看出,当s=N 且K ≥2 时,强于,因此,在处理块稀疏信号时,BgOMP 的约束条件较原始gOMP 的约束条件更加严格。 在本文的仿真实验中,块稀疏信号产生方法为:首先根据算法稀疏度,生成一个长度为K 的向量,其元素的数值符合高斯分布,然后计算K 个非零元可构成的块的个数k,从满足k 取值范围的整数中,随机选取一个值k´,将长度为K 的向量划分成为k´个块,最后将这些块随机插入长度为n-K 的零向量当中。 本文算法是经改进gOMP 而来,所以核心的仿真对比算法为gOMP。考虑到,gOMP 和BgOMP 均为需要已知稀疏度K 的匹配追踪算法,所以将业界较为著名的,同样也需利用该先验信息的几种匹配追踪算法也作为对比对象,包括OMP,ROMP,StOMP,SP,CoSaMP。 仿真中包含的参数有: (1)传感矩阵的维度,m、n,在后续所有仿真中,n=256; (2)信号的总稀疏度K 和块稀疏度k´; (3)特别地,对于gOMP 和BgOMP 还包括估计步长,N 和s; (4)对于拥有常数迭代停止条件的算法,设置为ε=10e-6; (5)仿真图片中,每一个概率数值均由1000次仿真实验得出。 仿真实验一对比各种算法在不同稀疏度场景下的经验重构概率,参数设置如下: (1)m=128; (2)5 ≤K ≤70,且取值间隔为5; (4)N 和s 均选 取2 和4 两 个 值。 从图2 中可以看出,仅对OMP 进行了简单修改的gOMP 算法性能明显优于SP 和CoSaMP 等复杂且具备精炼能力的算法,同时,能够看到在块稀疏场景下BgOMP 具有最优的重构概率,且在对应的步长选择情况下,较gOMP 具有明显的重构概率提升。当K=45 时,gOMP 的重构概率开始下降,而BgOMP 在K=50 时才下降。此外,在K=50 时,BgOMP仍然能以97%的重构概率恢复出原始信号,而gOMP 的重构概率以低于90%。 图2 不同稀疏度下的重构概率对比 仿真实验二对比BgOMP 和gOMP 的不同估计步长对经验重构概率的影响,与仿真实验一存在区别的参数如下: (1)仅对BgOMP 和gOMP 进行仿真; (2)s 和N 的取值包括,2、4、8、16。 从图3 中可以看出对应的步长情况下BgOMP重构性能均优于gOMP,且步长越小,重构性能越好。但是,小的步长必然导致更多的迭代次数,增加运算量,因此,步长需折中选择。不过,受篇幅限制,步长选择问题,此处不作过多讨论。 仿真实验三对比各种算法在不同测量值(测量值的数值等于y 的维度)下的经验重构概率,与仿真实验一存在区别的参数如下: (1)50 ≤m ≤100,且取值间隔为5; (2)K=20。 从图4 中可以看出在固定信号稀疏度的情况下,测量值数目相同时,BgOMP 的重构概率最高;在重构概率相同时,不论步长为何值,BgOMP 所需的测量值最少。在压缩感知框架中,通常认为测量值数目越少,算法能够适应的压缩比就越高,重构性能越好。此外,图4 中也能明显看出BgOMP 的性能优于gOMP。 图3 BgOMP 和gOMP 对比 图4 不同测量值下的重构概率对比 仿真实验四对比各种算法在不同稀疏度场景下的迭代次数,参数设置与仿真实验一完全相同。需要说明的是本次实验中,图中的每个数据通过1000次仿真实验中正确重构的实验次数统计而出。 从图5 中可以看出,OMP 需求的迭代次数均最多,等于稀疏度,符合该算法原理。StOMP 需求的迭代次数相对较少,但重构性能一般,K=35 时,重构概率极具下降,K=55 时,已无法重构信号。SP 和CoSaMP 这两种复杂的算法在稀疏度低时,重构概率高,需求的迭代次数少,但一旦稀疏度超过一个临界值,迭代次数将极具上升。 特别地,从图5 中可以看出,gOMP 和BgOMP是仅有的两种算法在稀疏度为70 的时候,还有部分仿真实验成功,迭代次数增长也较为平稳。同时,不难看出,相同情况下BgOMP 需求的迭代次数少于gOMP,且总的看来稀疏度越高越明显,这充分说明非零块的寻找是成功的,BgOMP 较gOMP 的改进优化是成功的。 图5 不同稀疏度下的迭代次数对比 本文针对压缩感知中的块稀疏信号重构问题,提出了块稀疏广义正交匹配追踪算法。该算法以原理简单,计算量小且重构性能优异的广义正交匹配追踪算法(gOMP)为基础,通过在gOMP 的迭代环节增加最大相关值相邻元素搜索步骤,实现了寻找信号非零块的功能,以简单的集合运算为代价,大幅提升了块稀疏场景下的重构概率。基于gOMP的理论分析表明若传感矩阵以一定条件满足RIP,那么BgOMP 必然能够重构信号,同时,数值仿真证明了BgOMP 是有效的,且较其他匹配追踪算法更适用于块稀疏重构场景。1 块稀疏信号模型
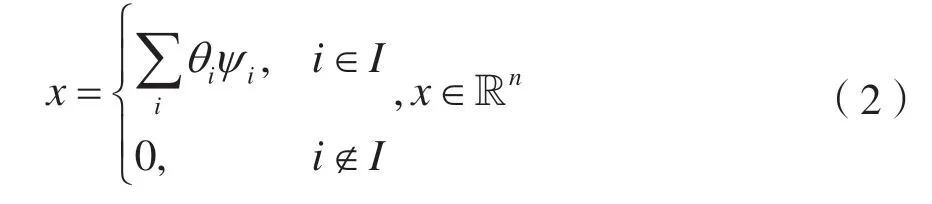

2 块稀疏广义正交匹配追踪算法

3 算法无失真重构条件



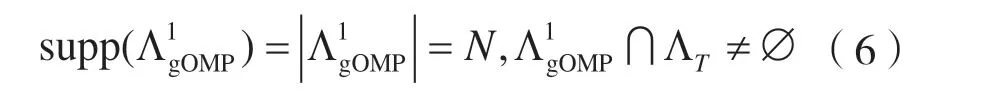
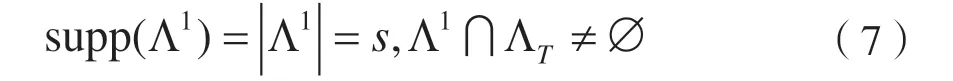

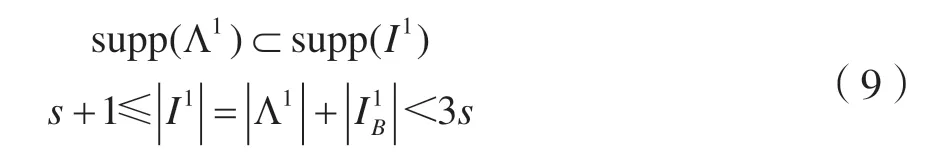


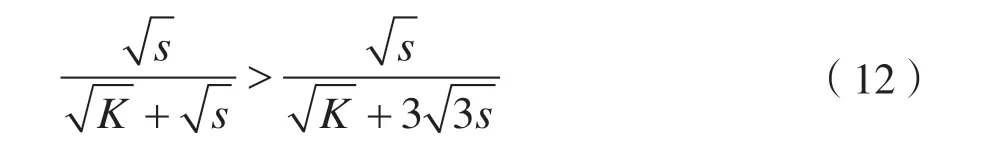
4 仿真验证
4.1 仿真条件设置
4.2 重构性能对比

5 结 语
