高中数学数列的解题技巧与方法

江苏省栟茶高级中学 刘晓燕

高中阶段的学习对于学生来说十分重要，在高中时期的学习成绩和学习能力都影响着学生今后的发展。高中数学的学习对学生来说有一定的难度，学生对于数学试题的解答有些无从下手，找不到正确的解题思路，没有对相应的问题形成相应的解题技巧。数列是高中数学中重要的学习内容，与函数、几何、不等式等都有很大的关联，并且在考试中占很大比重，因此，掌握好数列问题的解题技巧对于学生学习成绩的提高有很大的帮助。解题技巧在数学试题的解答中尤为重要，掌握了数学试题的解题技巧不但能够加深学生对知识点的理解，还能提高学生的解题能力，增强学生对数学理论知识的运用，提高学生的学习成绩。在数列问题中，找到合适的解题技巧，可以有效提高学生的解题能力和对知识的灵活运用，提高学生的数学学习效果。

一、利用数列基本概念求解

数列问题中有很多基础问题只需要利用数列的基本概念便可以解答，这种题型主要考查学生对于数列基本概念的记忆和理解，考查学生的基础知识，需要学生的基础知识扎实，困难的题目也只是在简单的题目基础上进行变形，数学问题的求解就是对各种公式定理的灵活运用，找出问题的正确答案，因此老师要加强对学生数列基本概念的教学，加深学生对数列基本概念的理解，在解答简单数列问题时，学生可以套用概念进行解答。在解决这些简单问题时，重要的是学生对于基本概念的正确理解，避免计算出现失误。

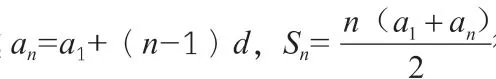
二、利用数列的性质求解

在数列问题中，有些问题不能通过已知条件直接得出答案，而是需要把已知条件通过其他形式表现出来，让学生自己发现，这类题目考查学生对于数列的性质的理解，学生需要对数列的性质有深入的了解并且能够灵活运用。老师在教学时，在学生理解基础知识的基础上引导学生总结出数列的性质，可以帮助学生对数列性质有更好的理解，在解决问题的过程中可以灵活使用，提高解决问题的效率。

例如：已知一个等差数列{an}，其中a2+a7=64，求a3+a4+a5+a6的和。在这类问题的解答中，考查学生对于等差数列的性质的掌握情况，学生要结合等差数列的性质，先找到解决问题需要的条件，再根据得到的已知条件将问题的答案计算出来。在等差数列中有这样一个性质：若m、n、p、q∈N＊，且m+n=p+q，则am+an=ap+aq。根据这个性质，我们可以知道a2+a7=a3+a6=a4+a5，所以a3+a4+a5+a6的和就等于2×（a2+a7）=128。在这类问题的解答中，不需要求出每一项的具体数值，利用数列的性质就可以得到最后的答案。

三、利用数列特殊方法求解

在数列问题中，有些问题都有着各自的特征，这些问题都有各自的解题技巧，在考试中这些问题也是最常见的，学生解答起来有一定的困难。例如求通项公式有常用的几种方法：an=Sn-Sn-1、累加法、累积法和构造法，求前n项和有常用的几种方法：错位相减法、分组求和法、裂项抵消法。在这些类型的数列问题中，每种方法都有自己适合的题型，学生在解答时要找到同类型题目的相似之处，运用正确的解题方法。例如，错位相减法适合用于由一个等差数列和一个等比数列的对应项之积构成的数列，那么这个数列的前n项和Sn可用此法来求。老师在教学过程中要加强学生对特定题型的练习，让学生熟悉之后可以灵活运用。

高中数学中数列试题有很多的解题技巧和方法，同时，数列问题在高中数学中有着非常重要的作用，老师在教学中要加强对学生解题技巧的指导，提高学生解决问题的能力，提高学生的数学成绩。