元认知——数学解题加速器

安徽大学高等教育研究所 刘 芳

在数学教育改革中，如何提高数学解题效率是重点，也是当今数学教育工作者研究的重点内容。数学解题顺利与否需要从其影响因素角度进行分析，元认知水平作为重要的因素之一，有重要的研究意义。认知主义学习理论认为，学生学的过程是认知结构的变化过程，是从初步形成到完善再到最终定型的一系列过程。其中最具代表性的，也最具权威性的则是弗拉维尔在《认知发展》中对“元认知”所做的明确定义：“元认知就是个体对自身认知过程的认知，包含对认知过程的认知和个体认知特点的认知，同时也包含个体对认知过程的主动调节。”简而言之，元认知是以“认知”为对象进行的“认知”，它以人的认知过程为研究对象，并对人的认知过程进行监测、调节等活动。认知心理学认为，问题解决是一种企图达到目标的尝试活动，被定义为任何受目标指引的认知性操作序列。可以看出，元认知与数学问题解决过程有着很大的联系。研究表明，数学活动中的元认知水平对数学解题有着重要影响，良好的元认知是数学解题的有效加速器。

一、元认知对数学解题的影响

当前国内在元认知对数学解题的影响的研究中，较为权威的观点是：元认知作为一种认知机构，在数学问题解决中是以计划、监控、调节、总结反思等来达到解题目标，指引解题者通过对问题外部表征的总结、解题策略的选择、解题思路的变换，最终达到顺利解决问题的目的。

元认知作用表现在数学解题的过程当中，主要体现在从最开始的审题阶段，解题者根据题目的表征方式在头脑中分析题目的含义并初步建构出具体的解题方案，并根据原有的知识和经验分析解题方案的可行性，为进一步实施方案做充分的准备。在这个过程中，元认知思想发挥了监控、计划、统领的作用。到最后的总结反思阶段，都能够看出元认知思想的重要作用。元认知过程实际上就是指导、调节认知的过程 ，选择有效认知策略的控制执行过程 ，其实质是人对认知活动的自我意识和自我控制。

二、元认知在数学解题中的案例分析

例1：现有16 个完全一样的正方体，请依据要求搭一搭，以符合下面的条件。

（1）搭出两个体积一样的立体图形；

（2）搭出两个立体图形，使一个的体积是另一个的三分之一。

分析：

（1）若要两个立体图形的体积一样，利用元认知知识和经验知道只要组成两个立体的正方体的个数一样就可以了（对认知过程进行控制和调节），所以两个立体图形均是由8 个小正方体构成的，立体图形的形状不唯一。

（2）首先要算出这两个立体图形是由几个立方体组合而成的。共有16 个正方体，要使其中一个的体积是另一个体积的三分之一，则使其中一个立体图形由12 个正方体组合而成，另一个立体由4 个小正方体组合而成就行了。这样的解题过程会形成新的经验，在下一次解题过程中起到作用，在这个过程中，数学元认知水平得到了提高。

分析：联系所学的知识和此类题目解决的经验，可将x4+x3-4x2+6x-25 分 拆 成：a（x-2）4+b（x-2）3+c（x-2）2+d（x-2）+e的形式。可得具体操作方式：待定系数法。

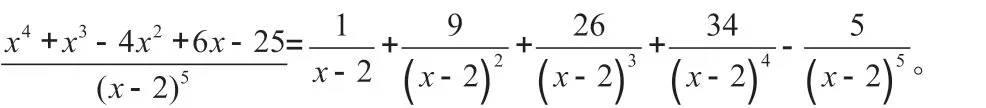
在数学解题过程中，元认知其实是相对独立的认知结构，是通过各种认知对应的行为活动，引领解题者对问题进行合理的表达，对策略进行采用，对思路进行更正，最终顺利解决问题。首先，学生在理解题目的初步阶段，利用元认知知识来引领其积极主动地和原来的数学结构和解题模式建立关系，建构正确的表征，并再一次重新审视该问题的内在特征和结构，给予其新的意义，为选择解题方案做准备。其次，在拟定解题方案阶段，利用元认知知识来使解题者找到合适的解题方法，同时，此过程的解题思想会迁移到以后的解题过程中。再次，在总结反思阶段，元认知思想则是让解题者积极对原来的行为进行总结，从成功和失败中学习，并将其归入现在的认知中，原有的经验和现在新的认知经验结合在一起。与此同时，思考其他更加有效的解决方法并总结解题经验，以此提升个体的元认知水平，为遇见新的问题提供服务，以进一步形成正迁移。

三、教师在数学教学中提高学生元认知水平的方法

第一，培养学生的自我意识进行监测。在数学教学活动中，教师要让学生感受数学认知活动的发生以及意义，体会运用不同方法学习的差异，让他们意识到数学学习活动包含有认知以及元认知过程，能够让他们自觉积极地去提升数学元认知水平来开展相应的元认知活动。第二，传授整合元认知知识，提升学生元认知水平。为让学生能够使用系统的知识为自己的数学学习提供便捷，为顺利解决数学问题打基础，教师应该传授完善的元认知知识，尽力丰富学生的元认知知识。