基于数据选择的非负自适应滤波算法

王紫璇

自适应滤波器是现代数字滤波器中重点的研究方向，和传统的滤波器不同，由于它可以在信号统计特性未知的情况下进行自适应学习，跟随信号与噪声的变化，因此目前已被广泛应用于信道均衡和回声消除等数字信号处理领域。

系统辨识是自适应滤波器的一个重要的方向，它可以用来估计系统的参数向量。自适应滤波器基本存在两种不同的方法，一是随机梯度下降法(Stochastic Gradient Approach)和最小二乘法(Least Square)，但它们的本质是求解无约束条件下的算法。非负性条件约束下的自适应滤波算法，本质上是求解条件约束下的最优化问题。条件约束下最优化问题是目前研究的热点，例如非负最小二乘[1]、非负矩阵分解[2]等应用。对于此类问题，常常用到广义化的拉格朗日乘子法，即KKT(Karush-Kuhn-Tucker)条件。

近年来，学者们对非负自适应滤波算法进行了较多的研究。2016 年，Chen 等人提出了非负最小均方算法(Nonnegative least mean square,NNLMS)以及一系列算法[3]，解决了非负最小二乘存在的批处理实时性差的问题，进而丰富了自适应滤波器的理论，拓展了自适应滤波器的研究范围。之后，学者们又提出了许多改进的NNLMS算法，例如指数非负最小均方算法(Exponential NNLMS)[4]和非负最小四阶矩算法(Nonnegative least mean fourth,NNLMF)[5-6]和基于零范数的非负最小均方算法(l0-NNLMS)[7]。

然而，这些算法均使用了全部的输入信号和噪声信号数据，使得其计算量较大。因此，学者们提出了一些基于数据选择的自适应滤波算法，例如DS-AP 算 法、DS-LMS 算 法[8]、DS-LMSN 算 法、DSLMSQN 算法[9]和DS-DLMS 算法[10]等，提升了自适应滤波算法的性能。但是，目前对于非负自适应滤波算法的数据选择研究尚属空白。本文将数据选择应用于非负自适应滤波算法当中。该算法首先以推导出的非负自适应滤波算法为基础，并利用数据选择的方法提升算法的性能。最终，采用计算机仿真试验来进行验证。实验证明，该算法在很好地减少计算量的同时，仍具有和原先算法同样的性能。

汽车和发动机在整个寿命期间如何减少故障、延长使用寿命、提高在有限时间内的工作质量始终是个难题。随着时间的发展，状态监控技术应运而生，它成为解决这个难题的重要手段和方法。状态监控不是判定结果(故障诊断)，而是养护和维修“注意”和“预测”。综合后的SAE状态监测概念列于表2，信息流程如图1所示。

1 算法推导

1.1 非负自适应滤波算法

图1 节点参数向量自适应辨识框图

自适应滤波算法正是通过最小化均方误差来进行迭代更新，使权值向量逼近未知系统权向量w*，进而得到最佳权值的。文献[3]求解出了在非负性约束条件下节点的定点迭代公式。在非负性约束条件下，系统的最优权向量满足：

根据上文可知，NNLMS 算法迭代公式为：

高潮的博客，田卓看得津津有味。高潮这次应聘的命运，也在这个时候悄然发生了改变。田卓翻看了几篇博文后，抬头对高潮说，你马上办理入职手续，策划方案就在公司写吧。

滑带土(T1d)④(图2、图3)：灰褐色，为粉质粘土和强风化泥灰岩碎石组成，可塑，很湿，无摇振反应，干强度及韧性中等，层厚0.40～0.50 m。岩土力学性质详见表1。

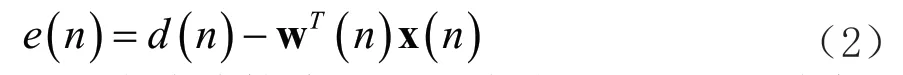
图1 为节点参数向量自适应辨识框图。在非负性约束条件下的系统辨识中，将未知系统的权向量表示为，M为系统的抽头个数。系统的期望信号满足：

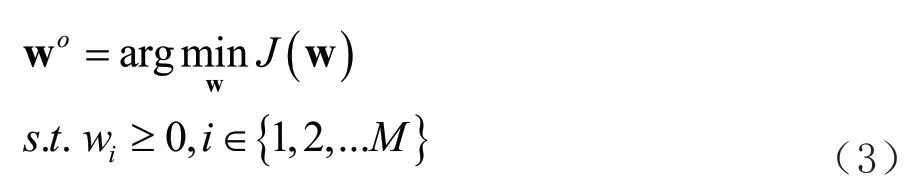
Η(k)的边界构成一个超平面。迭代时，我们需要检查之前 w(n)的估计值是否在约束集的外面[11]，即是否满足：

将式（4）代入式（5）可得：

非负性约束条件下的迭代公式推导基于以下两点：一、对于任何正定矩阵D，一定会有的方向与的 方向一致；二、一定可以得出基于以上推导，可得非负性约束条件下的节点迭代公式为[3]：

采用SPSS13.0统计学软件包把研究得到的数据建立数据库，使用χ2检验和t检验方法，计量资料采用均数方差表示，两组间比较，采用独立样本t检验，计数资料采用百分率表示且用χ2检验，P＜0.05为差异有统计学意义。

其中fi(w(n))为关于 w(n)的一个正值函数。文献[3]取为1/2，本文也采用这一数值，即：

其中，Dw(n)为以 w(n)的元素为对角元素的对角矩阵。

1.2 基于数据选择的非负自适应滤波算法推导

半夜两点，妻子从别墅的二层走到一层客厅，看到丈夫还在跟一帮赌友玩牌，就对他们说：“听着，能不能让我在自己的房子里安安静静地睡一会儿？”丈夫说：“轻点，亲爱的，现在这已经不是我们的房子了……”

其中J(w)为关于w 的代价函数，w 为系统最优权向量的估计值，wi为w 的第i个元素。文献[3]通过KKT(Karush-Kuhn-Tucker)条件，求解了在约束条件下的迭代公式。定义拉格朗日函数：

本组试验选取的数据为排水管壁试样直径d=100 mm、水力梯度相同的条件下，不同土体的稳定梯度比Gr值进行对比(如图6所示)。图6显示：在试样面积、水力梯度一致的条件下，与残积砾质黏性土相比，残积砂质黏性土的稳定梯度比Gr值增长了21%～30%，残积粉质黏性土的稳定梯度比Gr值增长了60%～69%，稳定梯度比Gr值随着黏性土中黏粒含量的增加而增大，且增大幅度较其他两种影响因素大。

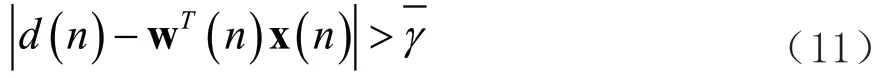
如果误差信号的绝对值在约束集外，则新的估计需要更新到约束集的最近边界。考虑先验误差：

通过图2可以看出，改进的Hardin-Drnevich模型可较好反映长河坝大坝心墙料和堆石料在动力条件下的材料特性。

浸没燃烧式气化器出口天然气(natural gas，以下简称NG)的温度和气化器水浴温度是SCV运行中非常重要的参数，其中出口NG温度是SCV运行的关键联锁因素[4]，它的稳定与否不仅关系到能否达到生产要求，而且关系到整个外输系统的稳定。而稳定的水浴温度对SCV的安全平稳运行至关重要:过高的水浴温度会导致排烟热损失增加、加速加热管等金属构件的腐蚀;而过低的水浴温度可能会导致水浴池内部分区域结冰，从而导致传热恶化。因此，需要将气化器出口NG温度和水浴温度控制在合理范围内。

根据上式推导可得

数据选择的好处是可以降低算法的计算复杂度，也就是说，只有当输出估计误差高于预先设定的上界时，才对于权值进行更新。算法的目标是设计w，使得误差的幅度的上界为预先设定的。如果设定的值太小，则可能使得算法收敛性能不好。如果设定的值太大，则达不到数据选择的要求。定义约束集：

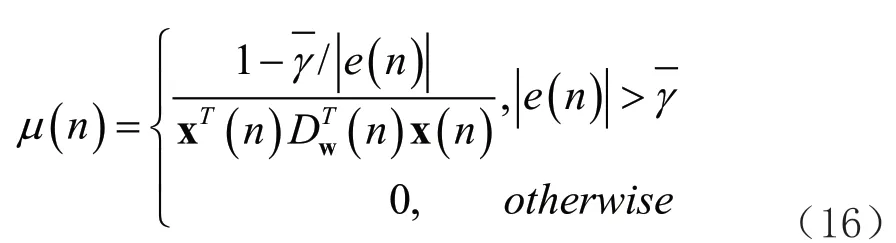
算法1 DS-NNLMS 算法初始化

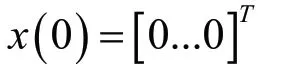
w(0)随机选择

当k≥0 时，计算：

2 计算机仿真

采用MATLAB 对算法进行仿真。未知系统的权值向量选为自适应滤波器的初始向量随机选择，所有实验都采用相同的权向量。采用归一化均方偏差NMSD 对算法的性能进行评估，其表达式为

所有的NMSD 曲线为独立学习200 次后取平均值的结果。本实验分别采用NNLMS 算法和DS-NNLMS算法对系统进行估计。NNLMS 算法选取固定步长µ0=0.08。输入信号和噪声信号均为零均值的高斯白噪声，取输入信号的方差为0.3，噪声信号的方差为10-3。输入信号经过未知系统后产生的没有噪声的期望信号和噪声信号的信噪比为21dB。根据文献[3]易知，经过迭代，非负自适应滤波器最优权向量应当更新为wo=[0.8,0.6,0,0.5,0.2]T。

图2 NNLMS和DS-NNLMS算法性能比较

由图2 可知，NNLMS 和DS-NNLMS 算法的收敛速度和稳态失调几乎相同。由计算机试验得出，DS-NNLMS 算法在4 000 次迭代中平均只运算了2 600次，减少了35%的计算量。而传统的NNLMS 算法则使用了全部的输入信号与噪声信号数据。因此，可以看出，DS-NNLMS 算法在不降低算法性能的同时，有效减少了迭代更新次数，这对于大规模数据的处理是非常有益的。

3 结论

本文将数据选择的方法应用到了非负自适应滤波算法中，并推导出了节点的迭代更新函数。计算机仿真试验表明，当输入信号和噪声信号均为高斯白噪声时，该算法可以在有效减少计算量的情况下，达到与原先的算法相同的性能。对于该问题，还可以有两个拓展的方向。一是可以继续减少计算量，二是将其应用至多任务自适应网络中，利用不同节点之间的协作增加算法的收敛速度、缩小稳态失调。对于这些问题，后续将进行进一步的研究。