基于色彩校正和融合的图像拼接算法

2020-04-25黄敏青

现代计算机 2020年9期

黄敏青

（四川大学计算机学院，成都610065）

0 引言

随着社会的发展和科学的进步，人们不再满足于视角有限的单幅图像所带来的信息，而是利用图像拼接技术将多幅图像拼接在一起从而获得拥有广视角、更多信息的图像。图像拼接技术是视频拼接的基础，广泛应用于视频监控、虚拟现实、航空航天等领域[1]。整个拼接流程通常为：通过相邻图像的重叠区域，进行特征提取得到特征点，再通过相似性度量找到匹配的特征点对，然后通过匹配的特征点对得到图像空间坐标变换参数，由坐标变换参数进行图像配准，最后将配准后的图像的重合区域按照一定的融合规则进行融合，得到拼接重构的平滑无缝图像。图像融合是图像拼接的关键技术之一，常见图像融合方法有直接平均融合法、加权平均融合法、多分辨率融合法、小波变换融合方法[2]等。某些情况下，因为摄像机自身的性能和工艺差异，以及自然环境的差异会导致在同一时刻获取到的图像存在一定的色彩差异，对融合效果有很大的影响[3]。为使拼接后的图像色彩统一，因此对图像进行色彩校正是非常有必要的。

1 理论背景

1.1 色彩空间

色彩空间指的是由三个独立的属性或变量组成的空间坐标，是进行色彩信息研究的理论基础。在我们的日常生活中，谈论色彩的时候一般指的是由红（Red）、绿（Green）、蓝（Blue）组成的RGB 色彩空间，RGB 色彩空间属于基色色彩空间，三分量R、G、B 之间的关联性很强，亮度信息在三个分量都有体现，由此衍生出了由色、亮组成的色彩空间：如YCrCb 色彩空间、HSL 色彩空间、YUV 色彩空间等。其中YCrCb 色彩空间来自于YUV 色彩空间[4]，Y 代表明亮度，Cb 和Cr 代表色度，Cb 具体为蓝色分量与明亮度之差，Cr 具体为红色分量与明亮度之差，二者相对没有联系，这样的特性赋予了YCrCb 色彩空间在图像亮度调节的优势。虽然不同的色彩空间的空间分量不一样，具有的特性也不一样，适用的领域也不一样，但是不同的色彩空间是同构的，它们之间可以通过数学公式互相进行转换。

RGB 与YCrCb 之间互相转换的公式如下：公式（1）是由RGB 空间转到YCrCb 空间，公式（2）是由YCrCb 空间转到RGB 空间。

1.2 图像融合

图像融合是整合配准后的图像信息，以达到图像过渡自然的目的，提高图像的质量[5]。主要有直接平均法、加权平均法、多分辨率融合法。

直接平均融合法方法平均了两幅图像重叠区域相对应的像素点对的像素值，将平均后的像素值作为融合后的像素值，计算方法如下所示：

其中，IL( i,j )和IR( i,j )分别为两幅待融合图像在重叠区域相对应的的某一点像素值，I( i,j )为融合后该点的像素值。该方法优点是简单，缺点是融合后的效果不好，最终的融合图像中会有明显的融合痕迹。加权平均融合法在实际运用中更为常见，将两幅图像重叠区域对应的像素值分别乘一定的加权值后，将加权后的像素值进行叠加得到的像素值作为融合后的像素值。计算方法如下所示：

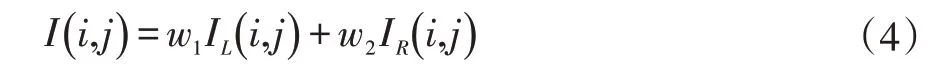
其中IL( i,j )和IR( i,j )分别为两幅待融合图像在重叠区域相对应的的某一点像素值，I( i,j )为融合后该点的像素值，w1，w2为权值，满足条件w1+w2=1，w1由1渐变到0，w2由0 渐变到1，由此实现重叠区域的平滑过渡。

多分辨率融合法[6]是由Peter J. Burt 在1983 年提出的，基于拉普拉斯金字塔（Laplacian Pyramid）变换的图像融合方法，后经研究者们不断创新，衍生出了多种多分辨率结构：高斯金字塔（Gaussian Pyramid）、拉普拉斯金字塔（Laplacian Pyramid）、小波金字塔（Wavelet Pyramid）、对比度金字塔（Contrast Pyramid）和梯度金字塔（Gradient Pyramid）等[7]。多分辨率融合方法的原理为：将图像分解为分辨率不同的子图像，再将子图像采用一定的融合规则分别进行融合，最后将融合后的子图像进行金字塔重构得到最终融合图像。该方法的融合效果好，但计算量大，耗时长，实时性差。

2 本文算法

2.1 色彩校正算法

为达到良好的校正效果，本文提出了YCrCb 空间下的色彩校正算法。算法的基本原理就是根据目标图像与参考图像各通道的平均值差异去调整目标图像各通道值。以下算法阐述以Y 通道为例，Cr，Cb 通道与此相同。假设目标图像（待校准图像）为ID，参考图像为IR。首先分别计算两图像重叠区域的Y 通道平均值，yR，yD。两者之间的差值ydif如下公式：

ydif=yR-yD（5）

如果直接简单地将ydif加到目标图像yD上，会因为两幅图重叠区域的亮度分布差异影响而达不到理想的校正效果。因此还需要根据两幅图亮度值较大的像素点所占的比例来调节ydif值。假设统计出两幅图重叠区域中高于各自平均值的像素点个数分别为CountD，CountR。由于两者重叠区域的总像素点个数是相同的，因此CountD，CountR就可以代表在两幅图中亮度值较大的像素点各自所占的比例。利用CountD，CountR得到更新后的ydif公式如下：

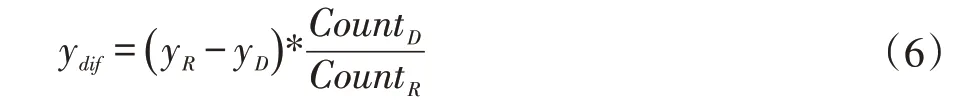
用CountD，CountR两者之间的比例来更新ydif的好处是可以使通道值的调节不受亮度分布差异的影响。以ydif大于0，即要提高目标图像y 通道值为例分析。当参考图像中高于平均值的像素点个数CountR大于目标图像中高于平均值的像素点个数CountD时，表明在参考图像中像素较暗的像素点受到较亮像素点的影响，相对于目标图像来说被提高了更多，实际上它并没有那么亮。因此在提高目标图像较暗像素点时应该减小ydif，即公式（6）表达的那样，这样才使得校正结果更接近参考图像。其他情况的分析类似。

当ydif大于0 时目标图像y 通道最终的校正公式如下：

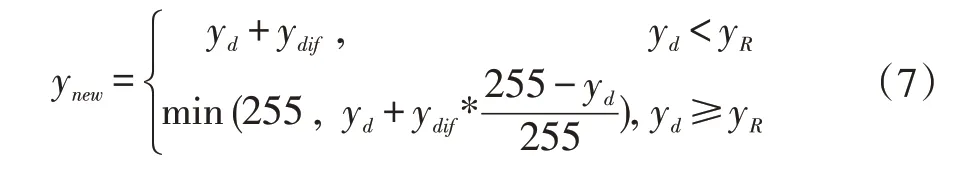
当ydif小于0 时目标图像y 通道最终的校正公式如下：

为应对通道值调整过饱和而失真严重的问题，公式中加入了相应的抑制处理：当ydif＞0 时：目标图像中较亮的像素点如果不加处理的直接加上ydif，此时可能会出现该像素点过亮而失真的情况。因此加入上述抑制手段后，当较亮像素点值越接近255，此时给它增加的值就越小。实验表明上述抑制过饱和的方法有效。

2.2 非线性融合算法

图像拼接中常用的融合方法有拼接缝融合，多分辨率融合，平均融合和线性融合。前两种方法功能强大，适用于复杂情况，但在实时性要求高的场景下就不太好用。后两种方法形式简单，适合一些相对理想场景的使用，实时性较强，但如果遇到较复杂场景时，难免会出现融合后的重合边界与重合区域过度不自然。由于线性融合时重合区域的边界一阶导数相对较大，因此使得边界处附近可能会出现不自然的过度。为应对上述情况，本文提出了一个新的非线性融合公式。假设wD，wR分别是左右两图重叠区域的融合权重。其中wD+wR始终等于1。融合后的像素点距重合区域左边界的距离占重合区域总宽度的比例为x ，xϵ[0 ,1] ，右图权重wR的计算公式如下：

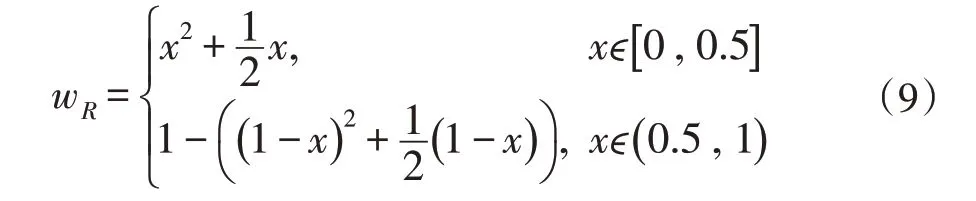
假设待拼接的图像左右分别为IL，IR，融合后的重合区域像素点为I 。按照公式（9）的权重分配，I 的计算公式为：

线性融合与非线性融合在待拼接图像重合区域的融合权重对比如图1。从图1 可以看出在重合区域的左右边界处，非线性融合权重的导数要小于线性融合，说明在边界处非线性融合具有更自然的过渡。在重合区域内，非线性融合相对线性融合也更具有灵活性。

图1 重合区域融合权重曲线对比图

2.3 拼接过程

本文的拼接算法具体流程图如图2 所示。

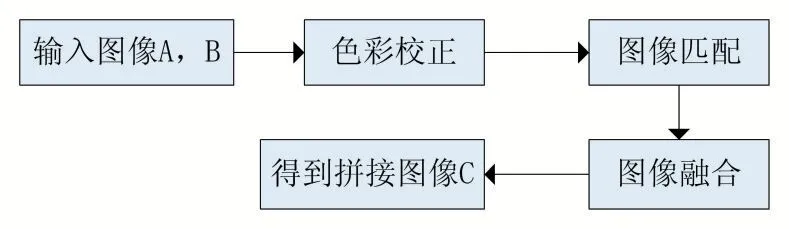
图2 拼接流程图

步骤1：输入图像A，图像B，进行色彩校正：将两幅图像转换至YCrCb 颜色空间，以图像A 为源图像，图像B 为目标图像，在该空间对图像B 的Y、Cr、Cb 通道分别进行调整，然后再将图像B 由YCrCb 颜色空间转换为RGB 空间；

步骤2：采用OpenCV 中的SIFT[8]算法查找图像A、B 的特征点并匹配，根据特征点得到变换矩阵H 后，可将图像B 乘以H 矩阵得到变换后的图B＇，由此得到重叠区域；

步骤3：对图A、图B＇按照上述非线性融合方法进行融合得到拼接图像C。

3 实验结果

本文分别从融合效果和色彩统一上进行了仿真实验，证明了本文算法的有效性。实验平台为Windows 10+VS 2019+MATLAB 2018b，计算机配置为Intel Core i5 3.2GHz 和 8GB RAM，使用的开源库为OpenCV4.1.0。图3 是分辨率均为480×640 的待拼接图像Image1 和Image2。

图3 待拼接图像

为了证明本文融合算法的有效性，仿真实验对上述待拼接图像采用直接平均融合法、线性加权融合法、本文非线性融合法得到的拼接结果如图4。

图4 融合实验结果

从图中可以观察到采用直接平均融合法得到的拼接图4（a）有明显的拼接痕迹，过渡极不自然；采用线性加权融合法得到的拼接图像图4（b）虽然没有明显的拼接痕迹，但是草地部分过渡偏生硬；而本文非线性加权融合法得到的拼接图4（c）没有痕迹且过渡较自然，效果较为理想。

以下实验是针对色彩差异的校正比较，在图3 中可以明显地看出两幅待拼接图像有色彩差异，在图4中的拼接结果均存在色彩不一致的问题，因此需要进行色彩校正。图5 是对Image1 进行校正后的拼接结果对比图，均采用的是非线性加权融合法，其中图5（a）是未进行色彩校正的拼接结果图，图5（b）是色彩校正后的拼接结果图。