土壤墒情预报模型构建及应用

蒋 颖

(铁岭市水利事务服务中心，辽宁 铁岭 112000)

0 引 言

目前，我国监测土壤墒情的方法分为人工和自动两种，人工监测方法是计算田间原状土壤在105℃±2℃干燥至恒重后，失水量与干燥土质量的百分比，它是直接监测土壤含水率的一种方法，同时也是国内外确定土壤水分的标准方法。

人工土壤干燥法精度高，时间长，一次测量通常需要6到10个小时。 因此，通常进行每十天进行监测，并且数据收集的频率较低。自动监测是将土壤水分传感器埋在庄稼地里，根据传感器输出的电信号与土壤水分之间的对应关系来获得土壤水分[2]。并且数据收集的频率高，快速且方便。

随着水文现代化的迅速发展，各级政府越来越重视干旱和减灾，对湿度监测的频率和数据精度的要求也越来越高，但目前的一些设备不能满足各级防汛抗旱指挥部门获取有关情况的需要[2]，导致报告数据的可靠性低，无法满足生产精度要求。

目前，我国旱情预报的方法，大多从探索土壤含水量的变化规律出发，研究作物需水量与土壤含水量及其他有关因素间的相关关系，来分析预报未来土壤水分的增减情况及其对作物生长的影响，以确定受旱程度。

由于影响土壤含水量的变化主要是由于降水，灌溉等因素的相对增加，而蒸发和农作物排放等因素已逐渐消退[3]，因此干旱预报增加增墒预报和退墒预报，这次研究主要以辽宁省营口市的墒情站为主。

2 退墒模型

2.1 退墒预报

2.1.1 退墒曲线原理

根据蒸发原理，在前期无雨天气状况情况下，土壤耕作层的水分逐渐向蒸发蒸腾消退，蒸发蒸腾与土壤含水量成正比关系，基本符合早期土壤水分指数的API水分计算方法，可以借用API模型，根据前期影响降雨量的来计算土壤含水率，其计算公式为：

θt+n+(αt+1αt+2…αt+n)θt

(1)

式中：θt为第t天土壤含水率；θt+n为第t+n天土壤含水率；αt+1-αt+n为t+1至t+n天的衰减系数。

在分析过程中，可以假设在两次连续监测水含量之间的时间间隔内，每日衰减系数是相同的。由此可将(1)式转化为：

θt+n=αnθt

(2)

式中：σ为t+1至t+n天的平均衰减系数。

2.1.2 衰减系数的计算

1)选择较为典型的干旱年份同时提取连续多日的无雨天数。

2)根据监测的相邻两次含水率来及随同降雨相隔日数。

2.1.3 退墒曲线的生成

1)根据季节(春季，冬季，夏季)对衰减系数系列进行分组。

2)通过衰减系数和相对应的土壤含水率，经过点群中心并绘制其关系线，最终得出典型站点的退墒曲线图。

1)找出连续无雨的时段,计算出间隔天数。

3)类似计算各相邻日期间的衰减系数，见表1。

表1 熊岳站衰减系数结果表

4)根据含水率和衰减系数画出散点图，见图1。

图1 熊岳站衰减系数散点图

5)点出趋势线和拟合公式，见图2。

图2 熊岳站衰减系数趋势线

6)根据趋势线画出最终的含水率与衰退系数相关图，见图3。

图3 熊岳站退墒曲线

2.2 土壤退墒特性

1)土壤退墒随季节变化较为明显，夏季温度相对高，相对湿度较小，这是一年中土壤蒸发相对最大的时段[5]。 此时，农作物需水量大，土壤流失加快，冬季温度低，土壤蒸发较小，农作物处于越冬期，需水量很小，因此冬季退墒较为缓慢， 在春季和秋季，提款率介于上述两者之间。营口地区冬季土壤处于封冻期，不进行土壤墒情检测，因此，未进行退墒计算。

2)衰减系数随初始土壤含水量的变化而变化，同期，当初始土壤含水量较大时，土壤供水充足，含水量下降较快，衰减系数较小[6]。相反，衰减系数越大，土壤水分衰减越慢，当初始土壤含水量接近枯萎系数时，消退几乎停止，其衰减系数接近1。因此，表明初始含水量与衰减系数成反比。

2.3 退墒曲线率定结果的验证

选取熊岳站2018年无降雨时段，5月13日至16日、7月8日至16日、7月24至25日进行验算，根据每时段监测所得的含水率，同时利用退墒系数计算，并将其与该时段中的实际监测值进行比较，见图4所示。

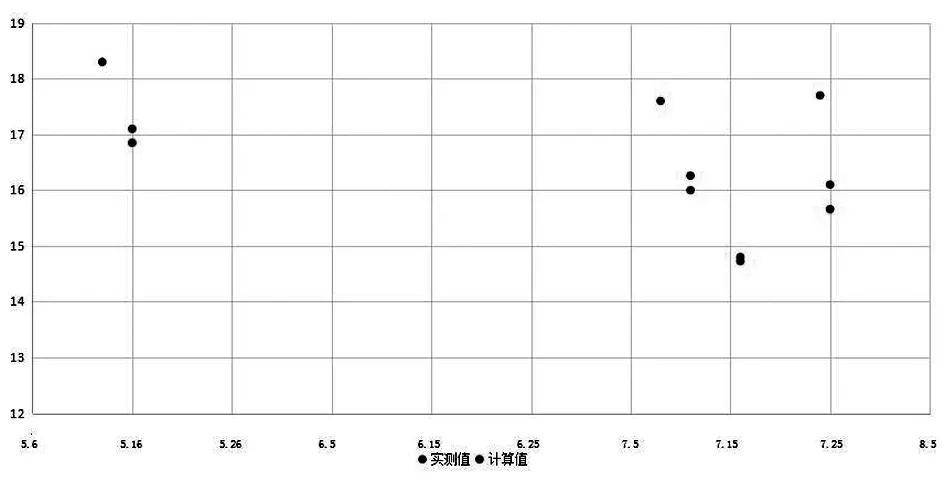
图4 熊岳站退墒曲线计算值与实测值对比图

根据分析可知，其平均绝对误差为1.6%，小于土壤相关规范中平均绝对误差为2%的要求。

3 增墒模型

3.1 增墒的物理过程

降水和灌溉逐渐增加导致了土壤的水分含量的相对增加[6]，称为土壤增墒，在田间，当以一定强度进行灌溉或产生降水时，地表水通过渗透进入土壤，成为土壤水，初始时表层首先吸收水，土壤水分开始增加，但随着降水或灌溉的继续，湿层开始向下层转移，下层的水分逐渐增加，土壤的初始吸水率相对较快，随着时间的加长，土壤含水量持续增加，土壤吸水率逐渐降低[7]，当降水或灌溉超过土壤的渗透强度时，地面可能会产生积水，并以通过地表径流的形式流出农田。

3.2 增墒预报

3.2.1 土壤含水量增值方程

计算公式如下：

ΔWs=F-f-E+Vg

(3)

F=P-Is-R

(4)

将式(3)带入式(4)，得到：

ΔWs=P-Is-R-f-E+Vg

(5)

式中：ΔWs为降水(灌溉)后土壤含水率的增加值，mm；F为总下渗量，mm；F为土壤深层下渗量，mm；E为计算ΔWs期的地表蒸发量，mm；Is为植物截流量，mm；R为径流深，mm；Vg为地下水补给量，mm。

3.2.2 增墒预报方案及经验公式

1)根据选取的墒情代表站所监测的土壤水分含量、蒸发量及降雨量和地下水深度资料等数据，绘制为降雨量P(mm)、平均含水率W(%) 及地下水深度h(m)、蒸发量E(mm)为纵坐标(暂时可不考虑蒸发量和地下水)，以时间为横坐标的墒情变化过程线图。2)在过程线图上选择降雨大于15mm的时段，摘取降雨P、降水量之前的土壤含水率Ws和土壤含水率增值ΔWs，绘制以雨前含水量Ws,o为参数的P-Ws,o-ΔWs三参数相关的增墒预报方案。

从P-Ws，o-ΔWs相关曲线可知，其曲线均为指数曲线，故在绘制每个站的相关图之后，可以在每个图上绘制与每个相关曲线相对应的ΔWs和P值点，通过图解方法获知获得各条曲线的经验公式，可将公式：P =aebΔWs，转换为：

ΔWs= ln(P / a)/ b，当某一天的土壤含水量和测得的降水量时，可以通过使用查图方法或经验公式获得站点降水后的土壤含水量，然后进行预测。

实例：

根据2018年营口地区熊岳、望宝山、汤池、徐屯四站资料，分析得出该区域的增墒曲线。

根据人工墒情站及所对应的降雨站，摘取降雨前后的次降雨和土壤含水量，如果6月4日有降水量，并且在6月1日和6月11日有实测含水率监测值，则将采用6月1日的含水率实测值通过退墒曲线推算出6月3日含水率； 根据6月11日的实测值，应用退墒曲线，对6月5日雨后的土壤水分进行反推。

1)对数据进行合理性检查，以消除异常值。

2)根据雨前的水分含量对提取的数据进行分类和分组。

3)以划分的组为单位，以P-ΔWs绘制趋势线。

4)分析趋势线的结果，以获得该区域或单个站点的P-Ws，o-ΔWs关系线。见图5。

图5 土壤含水趋势曲线

根据图6的趋势线，可以获取指数函数a和b的两个参数，见表3。

表3 营口地区不同雨前含水率对应的趋势线参数

计算公式ΔWs=ln(P/a)/b。

3.3 土壤增墒特性

通过对三参数相关性增墒预测方案P-Ws，o-ΔWs的分析，我们可以看到：

1)当雨前土壤含水量Ws，o相同时，降水量P增加，土壤含水量值也增加，反映出土壤含水量(Ws，o +ΔWs)开始相应增加；当土壤含水率达到不饱和状态时，ΔWs是P的增加函数。当土壤含水率低于田间持水量且降水量较小时，ΔWs等于有效降水量Pe，其增墒曲线末端近于平行的45o渐近线，其值大约等于植物截距Is； 当土壤含水量率增加或达到到田间持水量时，土壤含水量达到饱和状态。此后即使降水量再大，ΔWs也不在增加(即土壤含水量达到饱和后，ΔWs基本为一常数)，多余降水量除产生地面径流外，渗入土壤的水分向更深层下渗，形成重力水，补给地下水[7]。

2)在降水量P相同的情况下，雨前的ΔWs与土壤含水量Ws成反比，在P-Ws，o-ΔWs相关图中，增墒曲线簇Ws，o从左到右逐渐减小，即，当P为常数时，Ws,o较小，而ΔWs较大，反之亦然。 初始含水量越大，则降水转化为土壤水的百分比就越小，降雨损失也就越大，也就是说，雨水期的蒸发，径流和入渗随先前土壤含水量的增加而增加[8]。

4 预报模型验证

以熊岳、望宝山子站为例：选择2018年降雨资料，采用墒情预测模型计算每日水分含量，最后与测量值进行比较。 结果表明，误差在5%以内(见表4和表5)，满足要求。

表4 熊岳站7月1日至7月21日墒情预报模型预测结果

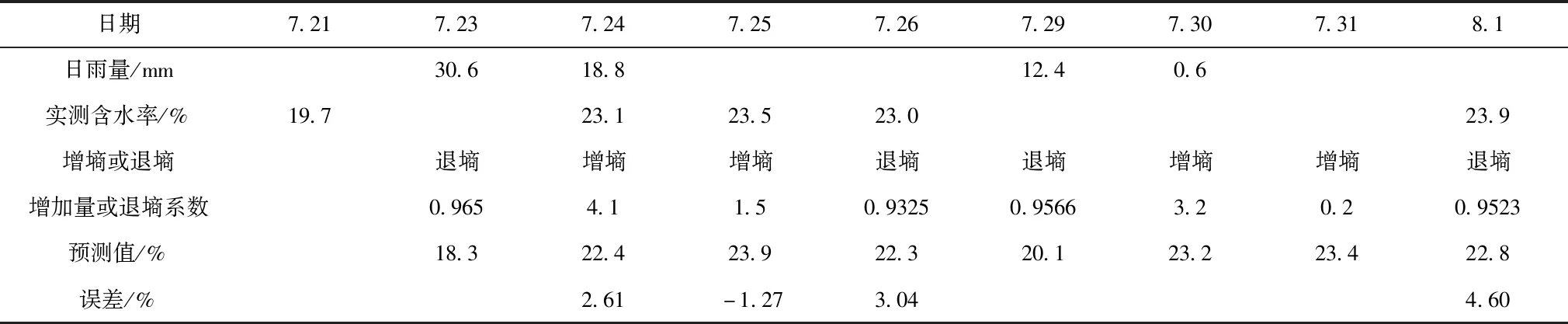
表5 望宝山站7月21日至8月1日墒情预报模型预测结果

实践证明，利用墒情预报模型可对今后一段时间内的含水率进行预测，可以满足生产应用的精度，为防旱减灾决策提供支撑。

5 结 语

1)预报结果准确与否很大程度上取决于预报方案的精度，而预报方案的精度高低又建立在充足可靠的墒情监测资料之上，因此，编制墒情预报方案时一定要搜集尽可能多的墒情资料[9]。另外一定要对数据进行筛选，尤其是异常数据，这是因为在实际观察中，由于使用了人工提取土壤，因此不可避免地会出现误差，并且可能是由于土壤中的水分含量过大而导致土壤水分含量过高，从而导致数据失真。另一方面异常数据对模型参数的计算结果干扰较大。

2)根据规定基本墒情站进行旬测，基本墒情资料缺少降雨前、后的加测资料，本次降雨前、后的含水率值采用退墒模型的预报值，增墒方案的精度受到一定影响[10]。今后应选择部分站增加测次，增加墒情资料，完善预报方案，提高预报精度。

3)墒情预报模型的分析很繁琐。 它既有经验又有技术含量，但是意义特别重大，可以归类为墒情基础研究，通过预测模型过滤自动监测数据，自动监测数据可以满足生产需求，减少了干旱期间人工加密监测的频率，节省了大量的人力物力[11]。

4)墒情预报模型用于预测连续无雨条件下或雨后短时间内的墒情条件，实际应用效果很好，该预测可为各级政府制定防旱减灾决策提供支持。