2019年北京高考物理24题引发的思考
2020-04-24赵芸赫马宇翰
赵芸赫 马宇翰
(1. 首都师范大学附属中学,北京 100048; 2. 北京计算科学研究中心,北京 100193)
2019年北京市高考物理试题的第24题描述了生活中一个常见的现象——雨滴在空气阻力和重力的共同作用下运动直至匀速下落的过程.该题在考察学生对能量守恒、牛顿第二定律的基础上,进一步考察了学生对动量定理与分子运动论的理解和运用.在第三问中,学生需要在将雨滴简化成垂直于运动方向面积为S的圆盘基础上,建立物理模型证明空气阻力f正比于下落速度v的平方.
在高考后,笔者注意到周围不少老师、学生都对题目提出了质疑.大家发现,用基于分子运动论的碰撞模型结合冲量定理,推得雨滴运动速度v在远低于空气分子热运动速度u时(这也是真实情境中的条件,雨滴下落速度一般为几米每秒,而室温下空气中分子热运动速度在400 m/s以上),所受空气阻力是正比于运动速度v的一次方而不是平方的[1,2]:
F=2Snm0uv=2ρaSuv.
这里n是单位体积分子数,m0是单个分子质量,S是物体在气流方向的横截面积,ρa=nm0是气体的密度.而高考标准答案在忽略气体分子无规则热运动的前提下,用流体模型得到了空气阻力和运动速度平方成正比的结论.人大附中胡继超老师和陈曦老师很快注意到这一问题,他们指出利用碰撞模型推导出空气阻力正比于雨滴运动速度平方这一结论的条件之一是假设了雨滴下落速度远大于气体分子的热运动速率[1].为了解决雨滴所受空气阻力到底是与速度一次方还是二次方成正比这一“矛盾”,胡老师等在他们的文中参考了流体力学中的奥辛近似阻力公式[3]
后,提出了一个包含物体运动速度一次、二次项的空气阻力表达式,但在其模型适用范围内,也只能得到雨滴受到阻力正比于其运动速度的结论.通过查阅文献可知[4-8],在分析雨滴以及气流中小球等物体运动所受的阻力时,被讨论得最多的即为粘滞阻力和压差阻力.那么,在日常生活中雨滴下落受到的阻力到底满足一次律还是二次律?前述碰撞模型和流体中两种阻力模型是否适用于真实的物理情境?为了解答这些问题,接下来本文从实际情境中雨滴的收尾速度的角度出发对上述问题进行了讨论.同时,本文还分析了碰撞模型在低速范围内所得出阻力与速度一次方成正比的结果失效的原因.
1 不同阻力模型预言的雨滴收尾速度
对于这样一个真实的物理情境,研究者可以从不同的角度建立模型.但是所建立的模型是否真的能解释这一现象,需要从实验的角度来加以验证.当然,进行定量的实验研究相对复杂,判断所运用的阻力模型是否适用的最简单的方式,就是比较生活中已有的客观事实和模型预言结果的一致性.首先将这一问题所涉及的一些物理量的数值列在下方.
· 雨滴的半径是毫米量级,从0.5 mm-2 mm不等,密度ρw=1000 kg/m3.
· 雨滴下落的收尾速度在几米每秒这个范围内.
· 大气中气体分子热运动速度约为400 m/s-500 m/s.
· 空气的粘度约为η=1.8×10-5Ns/m2,密度ρa=1.29 kg/m3.
· 重力常数9.8 m/s2.
在流体力学中,阻力的存在形式较多,如黏滞阻力、摩擦阻力、压差阻力等等[3].这些不同的阻力形式在物体在流场中运动所受的阻力中会有不同占比,这取决于问题情境所处的雷诺数区域.例如,在小雷诺数区域Re≪1,流场的粘性是阻碍物体运动的主要原因,此时黏滞阻力会其主要作用,如溶液中的布朗粒子所受的阻力就主要是黏滞阻力.而在较高雷诺数的区域,压差阻力和摩擦阻力会起主导作用,随着雷诺数的进一步增加,流场出现湍流,阻力形式变得很复杂而不存在简单的规律可以描述.
为了比较前文所述碰撞模型和流体中两种阻力模型的异同,将待检验的几种阻力模型对速度的依赖关系,以及它们所预言的雨滴下落速度(收尾速度)列入表1.

表1 不同阻力模型预言的雨滴收尾速度
其中CD是阻力系数,对于球形物体约为0.43[4].在这里,雨滴的收尾速度即是其在大气中运动末期在阻力和重力平衡下的匀速运动,由
mg=F(v).
给出.
从表1可以很直观地看出,黏滞阻力模型所预测的雨滴下落速度远高于雨滴下落的真实速度范围,而碰撞模型所给出的速度又过小.只有压差阻力所给出的速度与实际雨滴下落速度的范围匹配.在胡老师等人的文章中,他们认为“在雨滴速度足够小时,空气对雨滴的粘性占主导作用,阻力正比于速度;而雨滴速度足够大时,阻力才与速度平方成正比”.这里的速度的足够大与足够小,在他们文中是相比于气体热运动速度而言的[1].然而,对于在流体中运动物体所受阻力的来源,其判别应该是以雷诺数
这一无量纲参数为标准的.从上式可以看出,除了与相对运动速度有关,雷诺数还与流体密度、粘度,物体尺寸相关.因此,单纯从速度大小讨论雨滴受到何种阻力,是不严谨的.事实上,在雨滴下落过程中对应的雷诺数为Re≈1000远远超过了斯托克斯公式所适用的雷诺数Re≈1的区域,因此可以忽略雨滴所受黏滞阻力.同时也可以发现,高考标准答案所给出的结果
F∝nm0v2=ρaSv2.
与压差阻力的表达式形式上一致,仅差一个无量纲系数1/2CD~0.22.这表明高考标准答案所给出的结果可以给出与实际值匹配的雨滴下落速度范围.
2 碰撞模型失效的原因
那么,为什么利用碰撞模型给出的结果是反常的呢?接下来从气流能量的角度来进行分析. 考虑板面和气体之间的相对运动,对板而言气体以恒定速度吹来.对于气体分子而言,其速度可以写作整体流动速度和无规则热运动速度的和,即

则气流的总能量为
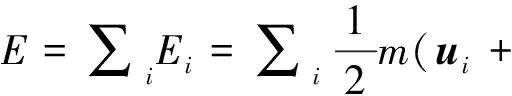


而在碰撞模型中,运动速度为ui的气体分子与板迎面碰撞后,速度反向并变为ui+2v.并且这一过程被假设发生在气体分子的平均自由程内,即不考虑气体分子的相互碰撞.这就导致了气体速率分布的变化,从而出现了表征气体内能与流动动能耦合的uiv项的出现.这只有对于十分稀薄的气体是成立的,而在空气中下落雨滴这一情境中的气体环境并不满足这一条件. 在真实情境中,气体分子碰撞板后会很快的与其它气体分子碰撞从而继续变为无规运动.因而在考虑具有定向运动速率的气体分子与板碰撞时,就不能忽略分子间的碰撞了.因此,用碰撞模型来解决雨滴在空气中受到阻力这一实际问题会变得很复杂,此时流体模型的便捷性就显示出来了.
在气流冲击圆盘的过程中,其整体流速在冲击板面后变为0接着沿两侧绕行至圆盘后方,这意味着气体受到来自圆盘的力F为
其中ΔM=ρaSΔl是在单位长度内和撞击到盘面的气流总质量,代入得到
这里假设圆盘运动缓慢,因而气流的密度可视为均匀.注意到,这一结论的导出不需要假设物体和气体的相对运动速度远大于气体分子的热运动速率.在气流流过圆盘的真实过程中,由于边缘效应和圆盘后方的气流涡旋存在,会在上述力中引入一个与雷诺数相关的阻力系数CD,最终得到圆盘给气流的作用力大小,即圆盘受到来自气流的阻力大小为
这就是前述的压差阻力,也可以从伯努利原理推导得出[9].
3 结论
综上所述,对本文的讨论给出如下总结.
物体在流体中以速度v运动时受到的阻力满足F(v)∝v还是F(v)∝v2由雷诺数Re决定,即由物体的尺寸,所处流体环境的密度和粘度共同决定.在Re≪1的区域,如在重力作用下在糖浆中下落的小球,流体的黏滞阻力起主要作用.而在雷诺数较大时,比如生活中常见物体所受空气阻力,均与速度二次方成正比,主要由压差阻力贡献;在气体平均自由程不够大时(非稀薄气体),用碰撞模型考虑物体在气体中受到的阻力是失效的;2019年北京市高考物理24题用流体模型证明空气阻力满足速度平方律是合理的,不需要假设板的运动远大于气体分子热运动速度.只需要说明“当板在气体中运动时,不考虑气体内能的变化”即可.
