压电倾斜镜迟滞非线性建模及逆补偿控制
2020-04-23李新阳
刘 鑫,李新阳,杜 睿
压电倾斜镜迟滞非线性建模及逆补偿控制
刘 鑫1,2,3,李新阳1,2*,杜 睿1,2
1中国科学院自适应光学重点实验室,四川 成都 610209;2中国科学院光电技术研究所,四川 成都 610209;3中国科学院大学,北京 100049
自适应光学系统中的压电倾斜镜通常是用来实时校正大气湍流引起的波前畸变,但压电倾斜镜的响应都有较大的非线性迟滞效应,大大降低了倾斜镜的到位精度,并且影响系统稳定性,制约了倾斜校正系统的带宽,因此需要对迟滞现象进行建模,通过建立的模型进行补偿。本文通过引入迟滞算子,使用贝叶斯正则化训练算法训练BP神经网络来构建压电倾斜镜迟滞模型,以中国科学院光电技术研究所自主研制的压电倾斜镜为对象开展了实验研究。最后的实验结果表明,通过BP神经网络构建的压电倾斜镜迟滞模型具有较准确的辨识能力,其中,方向的迟滞大小由6.5%降低到了1.3%,方向的迟滞大小由7.1%降低到了1.6%。
自适应光学;压电倾斜镜;迟滞效应;神经网络;迟滞算子
1 引 言
自适应光学技术主要用于克服和补偿大气湍流带来的影响[1],它通过实时探测和校正因大气湍流等引起的动态畸变来提高光学系统克服动态扰动的能力,改善光学系统的成像质量[2]。倾斜镜(tip/tilt mirror,TTM)是自适应光学系统中的重要元件,用来补偿大气湍流引起的倾斜像差。它利用高分辨率的压电驱动器驱动一块平面反射镜,使光束受控地产生快速、精确的小角度变化,具有位移分辨率高、响应速度快、功耗小等优点[3],广泛应用于自适应光学系统、目标指向、复合轴精密跟踪、激光束稳定系统、天文望远镜、激光雷达、激光束调整及空间光通信等领域[4-8]。
压电陶瓷材料自身存在固有的迟滞特性,实际应用时,这种迟滞特性会给压电倾斜镜的控制造成困难。压电陶瓷的迟滞特性是指压电陶瓷材料在升压和降压过程中两条位移曲线不重合,位移量不一致,存在位移差。其主要特点是:压电驱动器下一时刻的输出位移量不仅取决于当前时刻的输入电压和输出位移,而且与之前时刻的输入电压有关。研究表明,在无控制开环情况下,由迟滞曲线的不对称性造成的非线性跟踪误差达到15%以上。因此迟滞非线性的补偿对实现TTM高精度控制至关重要[3]。
针对压电倾斜镜的迟滞非线性特性,许多学者进行了深入研究,传统的迟滞非线性模型有Preisach模型[9-10],KP模型[11],PI模型[12]等,但这些模型在建模的过程中参数难以求解,计算复杂,也不利于工程实践上的应用。
本文通过引入迟滞算子进而构建BP(back propagation)神经网络模型,不仅简化了模型的建模过程,同时能够保证压电倾斜镜的开环控制迟滞补偿效果。
2 实验平台
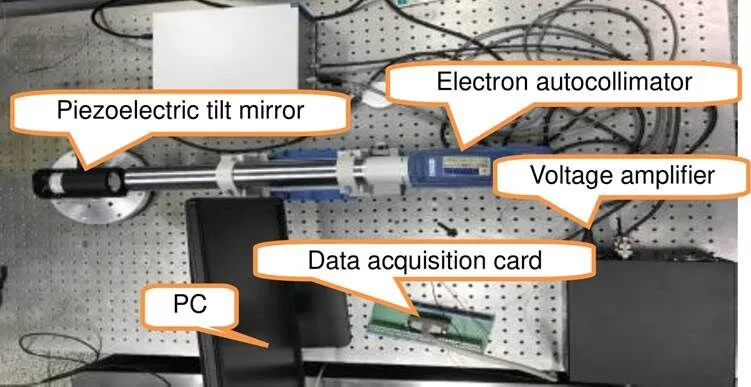
主要用到的实验器材包括:压电倾斜镜、电子自准直仪、电压放大器、上位机、数据采集卡。其中数据采集卡的型号是研华PCIE-1816卡,采样率为1 M/s;电子自准直仪是TRIOPTICS公司生产的,型号是T- AHS500-57,分辨率为0.1/秒,测量范围是-240²至+240²。电压信号放大器为中国科学院光电技术研究所自行研制的,输出电压范围为-500 V至500 V,分辨率为0.1 V。实验操作平台如图1所示。

图1 实验平台实物图
本文所研究的对象是中国科学院光电技术研究所自行研制的压电倾斜镜,其内部有四个压电陶瓷驱动器,能够驱动压电倾斜镜水平方向、竖直方向转动,转动的角度范围为-6¢至+6¢。压电倾斜镜的结构示意图如图2所示。
压电倾斜镜的输入是电压信号。计算机产生的数字信号经由内置于数据采集卡的D/A转换模块转换成模拟信号,再由信号发生器进行放大,然后驱动压电倾斜镜进行相关角度转动。压电倾斜镜产生的角度由电子自准直仪传感器测量后,再由采集卡采集模拟信号,传入计算机进行保存。实验过程中编写了同步输出电压与采集角度的程序。
研制出的压电倾斜镜具有迟滞特性,其迟滞性的大小为迟滞曲线的上升段与下降段之间的差值的最大值比上总角度范围,如下式所示:
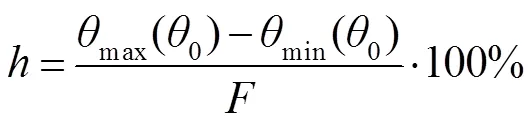
式中:为迟滞大小,0为期望角度,max为在期望角度值为0时上升段的输出角度,min为在期望角度值为0时下降段的输出角度,为总的输出角度范围。
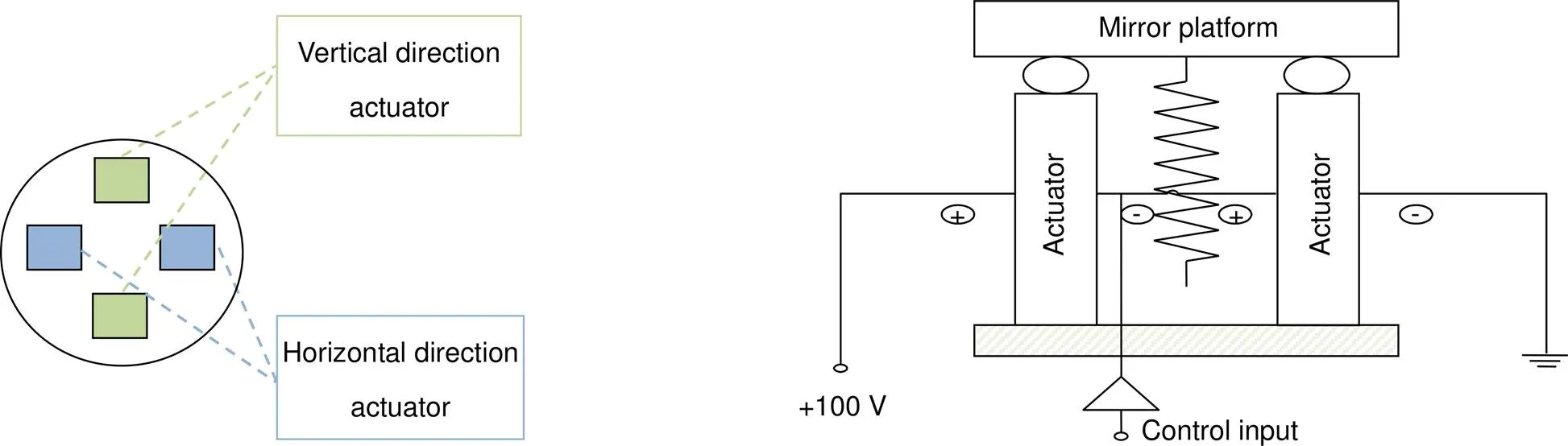
图2 (a) 倾斜镜驱动器位置示意图;(b) 倾斜镜结构示意图
3 构建神经网络模型
在建模方面使用了基于空间扩张的方法[13],通过引入迟滞算子来扩张压电倾斜镜输入电压在神经网络的输入空间,在三维空间上将迟滞的多映射转为一一映射,在变换后的空间上利用神经网络逼近这个一一映射从而建立一个基于神经网络的迟滞非线性模型,通过构建迟滞算子为神经网络输入引入一维特征。
迟滞正模型神经网络和迟滞逆模型神经网络的输入层均包含两个输入节点,一个输出节点,网络结构还包括一层隐藏层和一层输出层,如图3。采用贝叶斯正则化算法进行训练,使得网络的泛化能力更好。
图中D为误差值,W为输入层第个神经元与隐含层第个神经元之间的连接权,W为隐含层第个神经元与输出层第个神经元之间的连接权。
为了实现将压电倾斜镜输入电压与输出角度之间关系的二维空间转变为三维空间,引入的迟滞算子应该能够反应出压电倾斜镜的迟滞特性,也应具有迟滞特性。
参考文献[14]中的迟滞算子,本文所采用的迟滞正模型迟滞算子表达式为
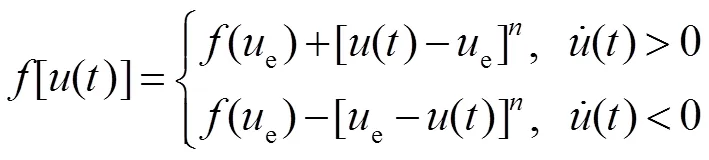
式中:()是当前迟滞算子的输入电压值;[()]是基本迟滞算子的当前输出;e是位于()之前的最近的一个输入电压极值;(e)是输入为e时的基本迟滞算子的输出;为指数。经过多组实测倾斜镜迟滞数据的正模型结果对比,针对倾斜镜迟滞正模型的指数为三次,更能描述本文所研究的压电倾斜镜的迟滞特性。压电倾斜镜逆模型角度与电压之间的关系也是一种多映射的关系,所以利用以上建立神经网络正模型的方法,通过引入逆迟滞算子来将迟滞的多映射转化为一一映射,从而建立起压电倾斜镜的逆模型。压电倾斜镜的输出角度值与逆迟滞算子作为神经网络的输入,压电倾斜镜的输入电压值作为神经网络的输出,进而构建压电倾斜镜的迟滞逆模型。对倾斜镜迟滞正模型迟滞算子进行求逆后,逆迟滞算子的表达式为
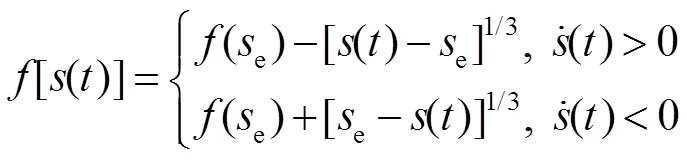
式中:()是当前逆迟滞算子的输入角度值,[()]是基本逆迟滞算子的当前输出;e是位于()之前的最近的一个输入角度极值;(e)是输入为e时的基本逆迟滞算子的输出。
4 模型验证
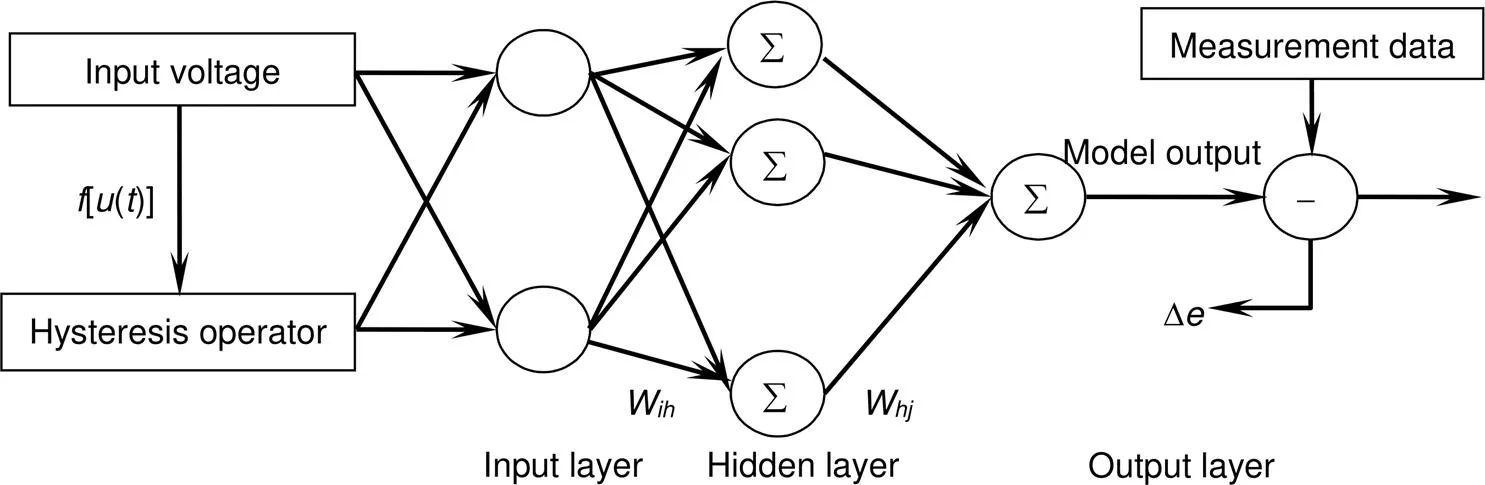
图3 压电倾斜镜迟滞神经网络训练结构
本文使用最小均方根误差(RMSE)和相对误差(RE)作为检验标准,对模型的效果进行定量的描述。最小均方根误差(RMSE)和相对误差(RE)的计算公式为
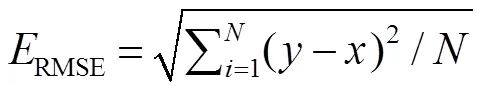
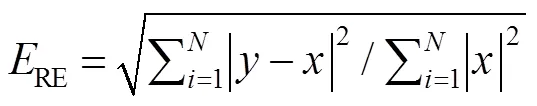
式中:是数据个数,是模型输出,是实际输出。
本文采用实测压电倾斜镜数据来对迟滞模型进行有效性验证以及对比。首先对方向进行验证。实验过程中,输入信号为幅值逐渐减小的正弦信号,电压范围为-320 V至320 V,驱动角度范围为-240²至240²。采集1200对实测数据,其中600对数据用来进行神经网络的训练,另外的600对数据进行对模型的验证,并与传统MPI[15]模型进行对比。
PI模型是通过对一系列play算子加权求和,来描述迟滞特性,play算子如图4(a)所示,而MPI模型是在PI模型的基础上再串联一系列非奇对称的deadzone算子,使得模型的辨识效果更好,deadzone算子如图4(b)所示。
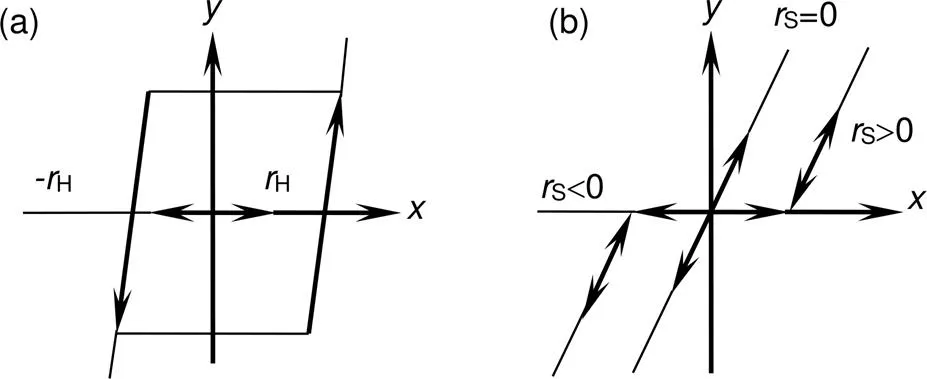
图4 (a) Play算子;(b) Deadzone算子
Play算子和deadzone算子的公式如式(6)和式(7)。
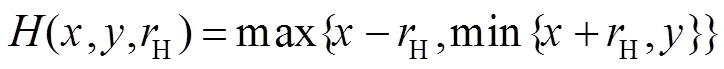
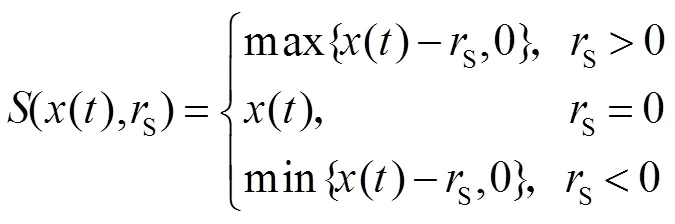
式中:H表示play算子的阈值,S表示deadzone算子的阈值。
Play算子和deadzone算子加权叠加的表达式为
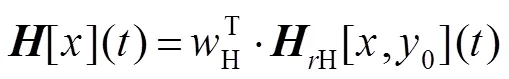
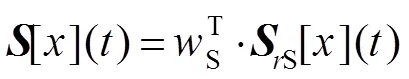
式中:H表示play算子的权重,S表示deadzone算子的权重,0是初始值。MPI模型的正模型和逆模型的表达式如式(10)和式(11)所示。
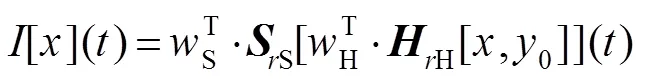
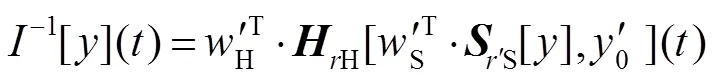
式中:[·]表示play算子,[·]表示deadzone算子,H表示play算子的阈值,S表示deadzone算子的阈值,H表示play算子的权重,S表示deadzone算子的权重,0是初始值。
实验中所采用的BP迟滞算子的正模型辨识误差范围在-0.048¢至+0.048¢,最小均方根误差RMSE为0.0106¢,相对误差为0.0119。实验中所采用的逆迟滞算子的模型辨识误差范围在-0.035 V至+0.03 V,最小均方根误差RMSE为0.0132 V,相对误差为0.0124。通过所建立的压电倾斜镜模型,对压电倾斜镜进行逆补偿控制,输入频率为1 Hz,最大幅值为320²,幅值逐渐减小的正弦期望角度信号,将经过逆模型计算得到的电压值提供给压电倾斜镜,采集测量得到压电倾斜镜的输出角度,分析跟踪误差,结果如图5所示。
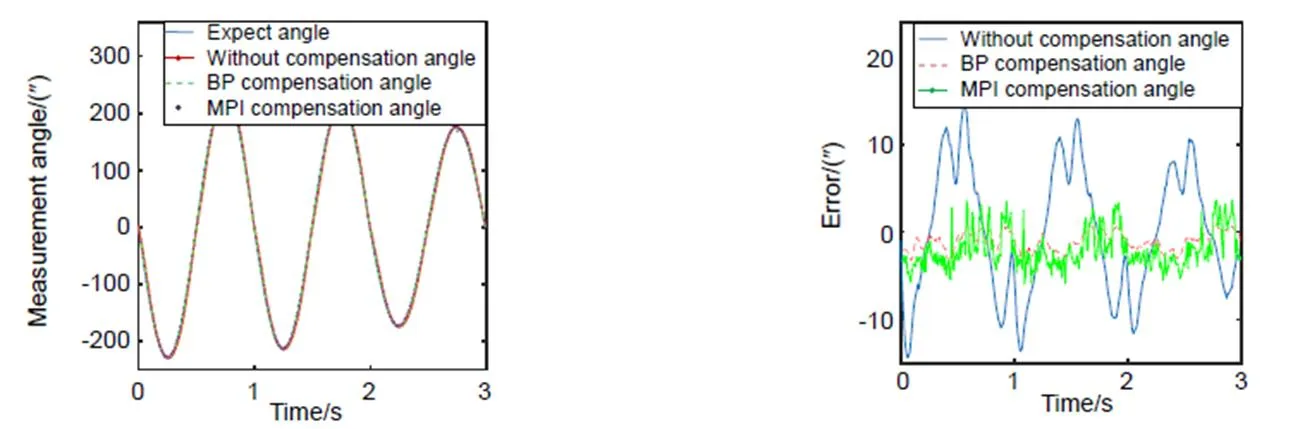
图5(a)中实线为期望角度输出,点线为未补偿实际角度输出,虚线为BP模型补偿后实际角度输出,点为MPI模型补偿后实际角度输出。图5(b)中实线为未补偿跟踪误差,虚线为BP模型补偿后跟踪误差,点线为MPI模型补偿后跟踪误差。可以看出,未补偿的跟踪误差介于-14²至+16²之间,模型辨识均方差RMSE为12.7²,相对误差为0.081,BP模型补偿后的跟踪误差介于-3²至+2²之间,模型辨识均方差RMSE为1.35²,相对误差为0.0137。MPI模型补偿后的跟踪误差介于-5²至+4²之间,模型辨识均方差RMSE为2.78²,相对误差为0.042。图6(a)中虚线为未经过逆模型补偿的迟滞曲线,迟滞大小为6.5%,实线为经过BP逆模型补偿后的迟滞曲线,迟滞大小为1.3%,点线为MPI逆模型补偿后的迟滞曲线,迟滞大小为2.21%。图6(b)为方向期望角度与输出角度之间迟滞大小的示意图,横轴为期望角度对(同一输入周期内,同一期望角度对应两个测量角度值,对表示第几对期望角度的测量角度)。
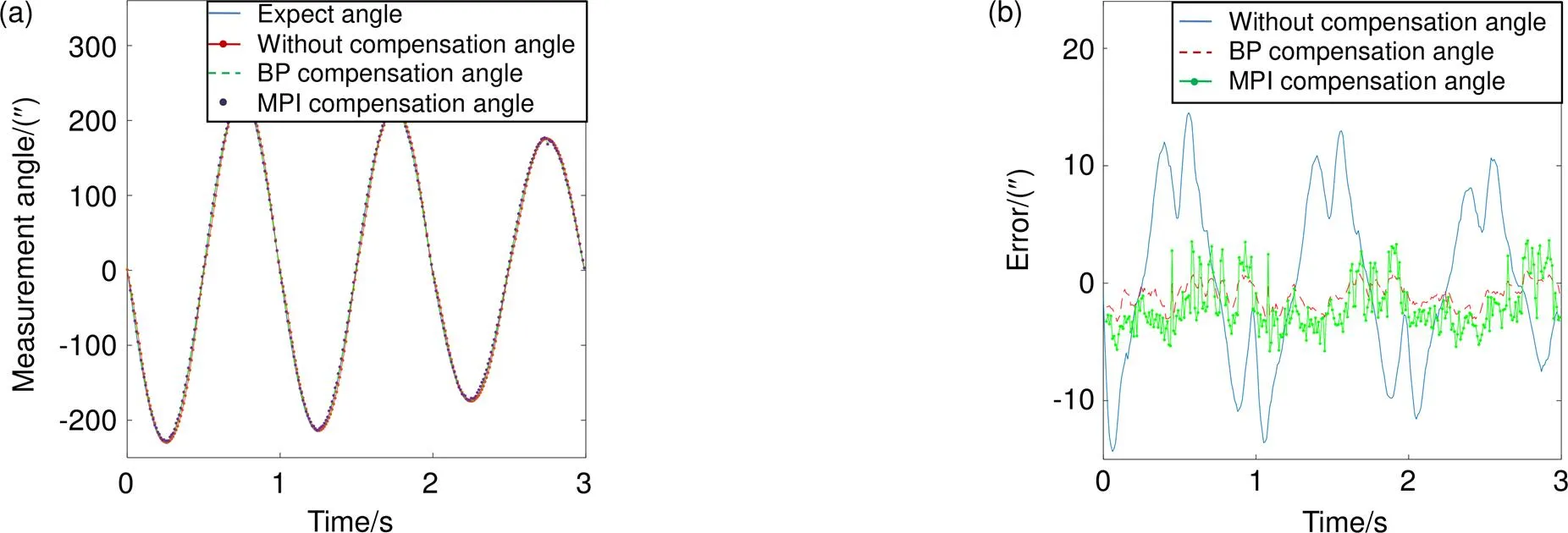
图5 压电倾斜镜(X方向)迟滞补偿示意图。(a) 角度跟踪示意图;(b) 误差示意图
接下来进一步对压电倾斜镜方向迟滞现象逆模型进行验证。实验过程中,输入信号为幅值逐渐减小的正弦信号,电压范围为-280 V至280 V,驱动角度范围为-216²至216²。采集1200对实测数据,其中600对数据进行神经网络的训练,另外的600对数据进行模型验证。
实验中所采用的BP迟滞算子的正模型辨识误差范围在-0.048¢至+0.05¢,最小均方根误差RMSE为0.0112¢,相对误差为0.0134。所采用的逆迟滞算子的模型辨识误差范围在-0.04 V至+0.04 V,最小均方根误差RMSE为0.0148 V,相对误差为0.0142。通过所建立的压电倾斜镜模型,对压电倾斜镜进行逆补偿控制,输入频率为1 Hz,最大幅值为216²,幅值逐渐减小的正弦期望角度信号,经过逆模型计算得到的电压值提供给压电倾斜镜,采集测量得到压电倾斜镜的输出角度,分析跟踪误差,结果如图7所示。
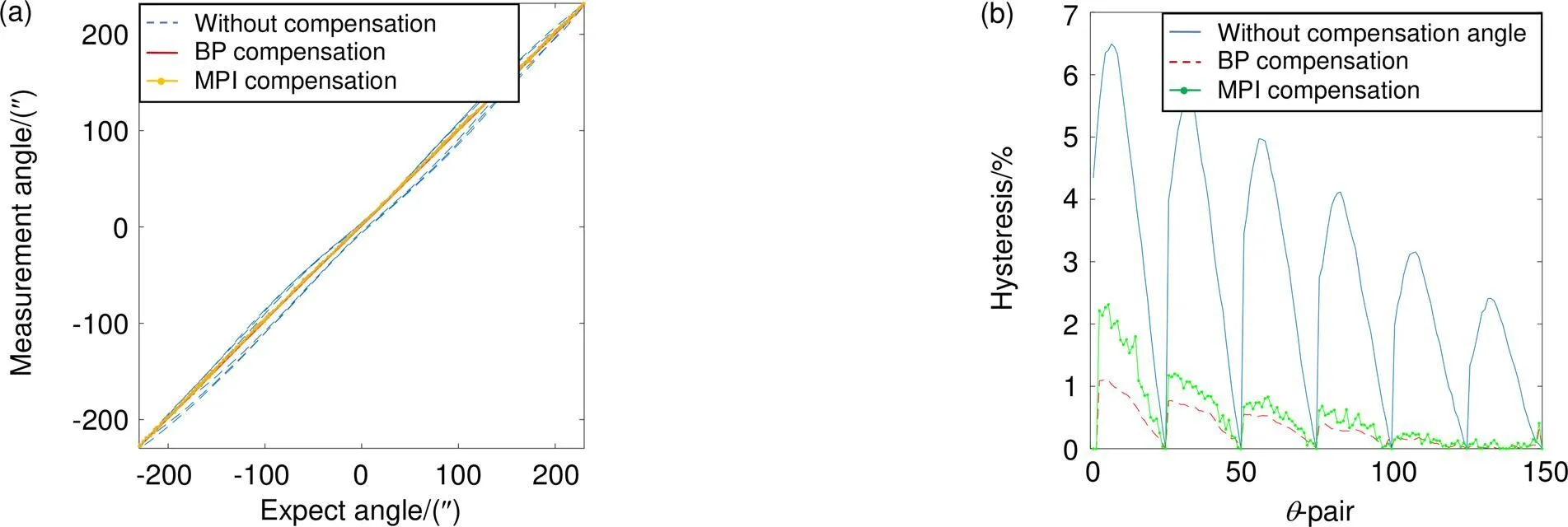
图6 (a) 压电倾斜镜X方向迟滞补偿对比图;(b) X方向迟滞大小示意图
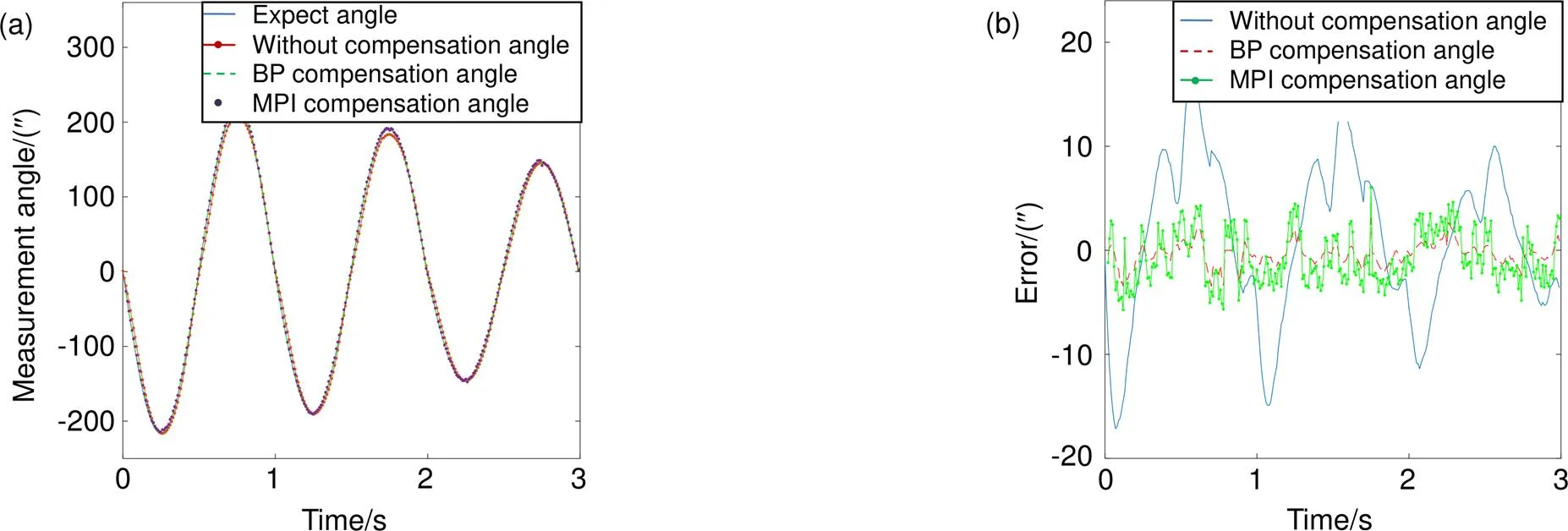
图7 压电倾斜镜(Y方向)迟滞补偿示意图。(a) 角度跟踪示意图;(b) 误差示意图
图7(a)中实线为期望角度输出,点线为未补偿实际角度输出,虚线为BP模型补偿后实际角度输出,点为MPI模型补偿后实际角度输出。图7(b)中实线为未补偿跟踪误差,虚线BP模型补偿后跟踪误差,点线为MPI模型补偿后跟踪误差。可以看出,未补偿的跟踪误差介于-16²至+16²之间,模型辨识均方差RMSE为14.3²,相对误差为0.093,BP模型补偿后的跟踪误差介于-3²至+3²之间,模型辨识均方差RMSE为2.47²,相对误差为0.0156;MPI模型补偿后的跟踪误差介于-6²至+6²之间,模型辨识均方差RMSE为5.12²,相对误差为0.0356。图8(a)中虚线为未经过逆模型补偿的迟滞曲线,迟滞大小为7.1%;实线为经过BP逆模型补偿后的迟滞曲线,迟滞大小为1.6%;点线为经过MPI逆模型补偿后的迟滞曲线,迟滞大小为2.89%。图8(b)为方向期望角度与输出角度之间迟滞大小的示意图,横轴为期望角度对。
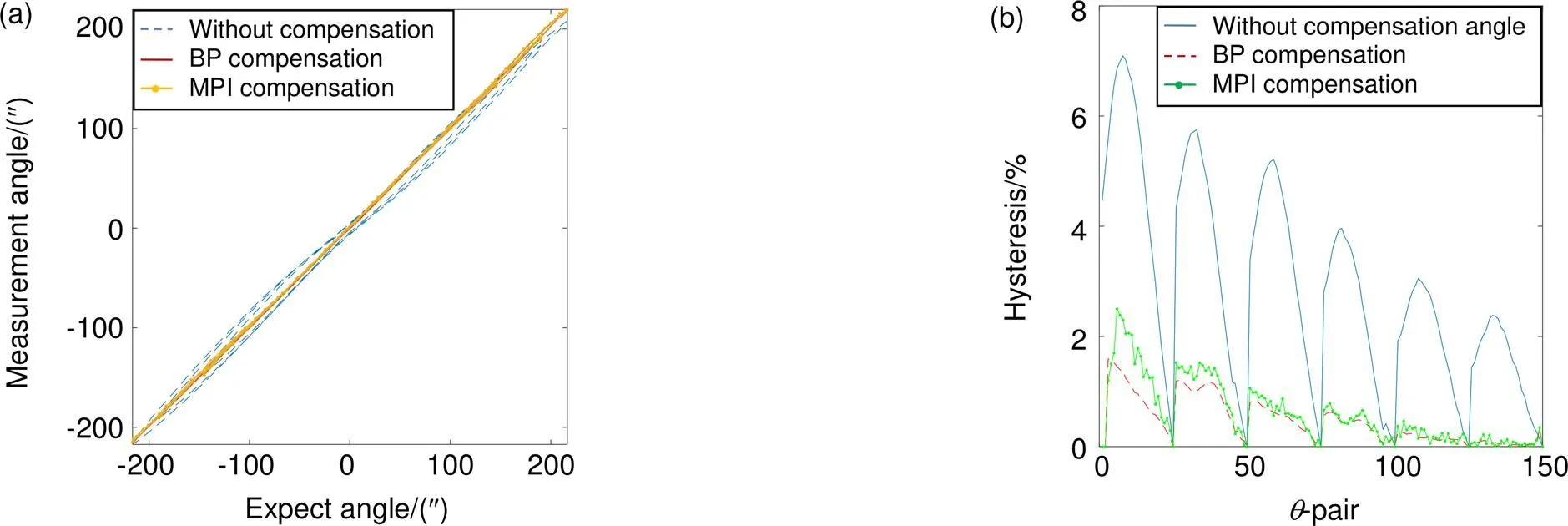
图8 (a) 压电倾斜镜Y方向迟滞补偿对比图;(b) Y方向迟滞大小示意图
从实验结果可以看出,所建立的模型对于压电倾斜镜在方向和方向的非线性现象的补偿效果较好,对比结果如表1所示。
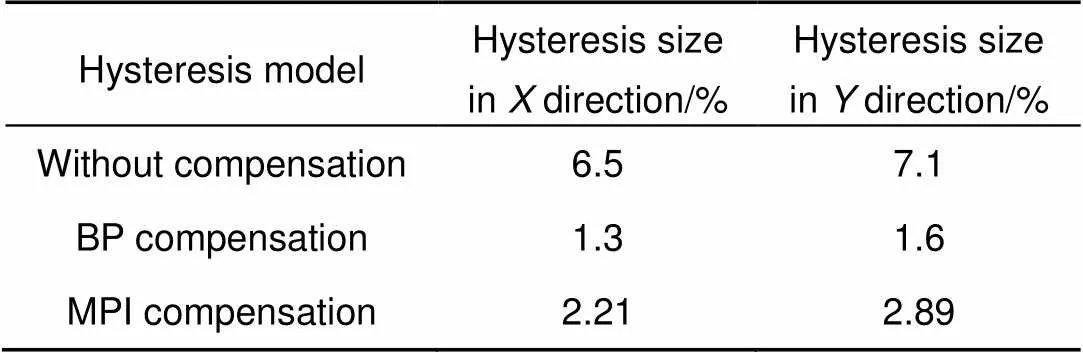
表1 迟滞补偿结果
5 结 论
针对压电倾斜镜的迟滞非线性,引入了迟滞算子,建立了基于BP神经网络的迟滞模型,建模方法相较于传统的MPI模型补偿结果更好。最后的逆补偿实验结果表明,方向的迟滞非线性由6.5%降低到了1.3%,方向的迟滞非线性由7.1%降低到了1.6%,对于中国科学院光电技术研究所研制的压电倾斜镜,所建立的模型具有较为准确的辨识能力。
[1] Tyson R K.[M]. Bellingham, Washington: SPIE Press, 2000.
[2] Wang Y K, Hu L F, Wang C C,. Modeling and control of Tip/Tilt Mirror in liquid crystal adaptive optical system[J]., 2016, 24(4): 771–779.
王玉坤, 胡立发, 王冲冲, 等. 液晶自适应光学系统中倾斜镜的建模与控制[J]. 光学精密工程, 2016, 24(4): 771–779.
[3] Wang C C, Hu L F, He B,. Hysteresis compensation method of piezoelectric steering mirror based on neural network[J]., 2013, 40(11): 1113001.
王冲冲, 胡立发, 何斌, 等. 基于神经网络的压电倾斜镜磁滞补偿方法研究[J]. 中国激光, 2013, 40(11): 1113001.
[4] Perez Arancibia N O, Chen N, Gibson J S,. Variable-order adaptive control of a microelectromechanical steering mirror for suppression of laser beam jitter[J]., 2006, 45(10): 104206.
[5] Tan F F, Chen X T, Yao B D,. Tilt correction system for laser atmospheric propagation[J]., 2011, 40(3): 429–432.
谭逢富, 陈修涛, 姚佰栋, 等. 激光大气传输倾斜校正系统[J]. 红外与激光工程, 2011, 40(3): 429–432.
[6] Wang H H, Chen F B, Shou S J,. High precision electro-optical tracking system based on fast steering mirror[J]., 2010, 31(6): 909–913.
王红红, 陈方斌, 寿少峻, 等. 基于FSM的高精度光电复合轴跟踪系统研究[J]. 应用光学, 2010, 31(6): 909–913.
[7] Kluk D J, Boulet M T, Trumper D L. A high-bandwidth, high-precision, two-axis steering mirror with moving iron actuator[J]., 2012, 22(3): 257–270.
[8] Xu F F, Ji M, Zhao C S. Status of fast steering mirror[J]., 2010, 31(5): 847–850.
徐飞飞, 纪明, 赵创社. 快速偏转反射镜研究现状及关键技术[J]. 应用光学, 2010, 31(5): 847–850.
[9] Mayergoyz I D.[M]. New York: Springer-Verlag, 1991.
[10] Hu H, Mrad R B. On the classical Preisach model for hysteresis in piezoceramic actuators[J]., 2003, 13(2): 85–94.
[11] Banks H T, Kurdila A J. Hysteretic control influence operators representing smart material actuators: identification and approximation[C]//, Kobe, Japan, 1996: 3711–3716.
[12] Su C Y, Wang Q Q, Chen X K,. Adaptive variable structure control of a class of nonlinear systems with unknown Prandtl-Ishlinskii hysteresis[J]., 2005, 50(12): 2069–2074.
[13] Zhao X L. Modeling and control for hysteresis systems based on hysteretic operator[D]. Shanghai: Shanghai Jiao Tong University, 2006.
赵新龙. 基于迟滞算子的迟滞非线性系统建模与控制研究[D]. 上海: 上海交通大学, 2006.
[14] Ma L W. Modeling and control for sandwich hysteresis systems[D]. Shanghai: Shanghai Jiao Tong University, 2007.
马连伟. 三明治迟滞非线性系统的建模与控制研究[D]. 上海: 上海交通大学, 2007.
[15] Kuhnen K. Modeling, identification and compensation of complex hysteretic nonlinearities: a modified Prandtl-Ishlinskii approach[J]., 2003, 9(4): 407–418.
Modeling and inverse compensation control of hysteresis nonlinear characteristics of piezoelectric steering mirror
Liu Xin1,2,3, Li Xinyang1,2*, Du Rui1,2
1Key Laboratory of Adaptive Optics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China
(a) Contrast diagram of the X direction hysteresis compensation of piezoelectric steering mirror;(b) The diagram of hysteresis size in X direction
Overview:Piezoelectric tilt mirror in adaptive optics system is usually used to correct the wavefront distortion caused by atmospheric turbulence in real time. However, piezoelectric ceramic materials often have inherent hysteretic characteristics. In practical application, such hysteresis makes the control of piezoelectric tilt mirror difficult. The hysteretic characteristic of piezoelectric ceramics is that two displacement curves of piezoelectric ceramics do not coincide with each other in the process of pressure rise and pressure fall. The main characteristic is that the output displacement of the piezoelectric actuator at the next moment depends not only on the input voltage and output displacement at the current moment, but also on the input voltage at the previous moment. The results show that the nonlinear tracking error caused by the asymmetry of hysteresis curve is more than 15% in the case of uncontrolled open loop. Therefore, non-linear hysteresis compensation is essential to achieve high accuracy control of tip/tilt mirror (TTM), so the hysteresis phenomenon needs to be modeled and compensated by the established model. Many scholars have studied the hysteresis and non-linearity of piezoelectric tilt mirror. The traditional hysteresis and non-linearity models include Preisach model, KP model, PI model, etc. However, the parameters of these models are difficult to solve and the calculation is complex, which is not conducive to the application in engineering practice. In this paper, the hysteresis model of piezoelectric tilt mirror is constructed by introducing the hysteresis operator and using the Bayesian regularization training algorithm to train BP neural network. The final experimental results show that the hysteresis model of piezoelectric tilt mirror constructed by BP neural network has a relatively accurate identification capability, where the hysteresis size in thedirection is reduced from 6.5% to 1.3%, the identification error range of positive model is between -0.048 arcmin to +0.048 arcmin, the minimum root-mean-square error (RMSE) is 0.0106 arcmin, and the relative error is 0.0119. The model identification error range of the inverse hysteresis operator used in the experiment is -0.035 V to +0.03 V, the minimum RMSE is 0.0132 V, and the relative error is 0.0124. The hysteresis in thedirection was reduced from 7.1% to 1.6%. The positive model identification error range of BP hysteresis operator adopted in the experiment was -0.048 arcmin to +0.05 arcmin, the minimum RMSE was 0.0112 arcmin, and the relative error was 0.0134. The model identification error range of the adopted inverse hysteresis operator is -0.04 V to +0.04 V, the minimum RMSE is 0.0148 V, and the relative error is 0.0142. For the piezoelectric tilt mirror developed by Institute of Optics and Electronics, Chinese Academy of Sciences, the model established has relatively accurate identification ability.
Citation: Liu X, Li X Y, Du R. Modeling and inverse compensation control of hysteresis nonlinear characteristics of piezoelectric steering mirror[J]., 2020,47(4): 180654
Modeling and inverse compensation control of hysteresis nonlinear characteristics of piezoelectric steering mirror
Liu Xin1,2,3, Li Xinyang1,2*, Du Rui1,2
1Key Laboratory of Adaptive Optics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China
In the adaptive optics system, the piezoelectric steering mirror(tip/tilt mirror, TTM) is usually used to correct the wavefront aberration caused by atmospheric turbulence in real time. However, the response of the piezoelectric tilting mirror has large nonlinear hysteresis effect, which greatly reduces the precision of the tilting mirror in place, affects the stability of the system, and restricts the bandwidth of the skew correction system. Therefore, the hysteresis phenomenon needs to be modeled and compensated by the established model. In this paper, hysteresis operator is introduced and using Bayesian regularization training algorithm to train BP (back propagation) neural network to construct hysteresis model of piezoelectric steering mirror. Then experimental study was conducted on a piezoelectric steering mirror developed by Institute of Optics and Electronics, Chinese Academy of Sciences. The final experimental results show that the hysteresis model of piezoelectric steering mirror constructed by BP neural network has more accurate identification capability, the hysteresis size in thedirection decreased from 6.5% to 1.3% and that in thedirection decreased from 7.1% to 1.6%.
adaptive optics; piezoelectric steering mirror; hysteresis; neural network; hysteresis operator
National Key Research and Development Program (2017YFB0405100)
* E-mail: xyli@ioe.ac.cn
TP29
A
刘鑫,李新阳,杜睿. 压电倾斜镜迟滞非线性建模及逆补偿控制[J]. 光电工程,2020,47(4): 180654
10.12086/oee.2020.180654
: Liu X, Li X Y, Du RModeling and inverse compensation control of hysteresis nonlinear characteristics of piezoelectric steering mirror[J]., 2020, 47(4): 180654
2018-12-13;
2019-08-06基金项目:国家重点研发计划(2017YFB0405100)
刘鑫(1994-),男,硕士研究生,主要从事自适应光学中压电陶瓷驱动器及倾斜镜建模、人工智能方面的研究。E-mail:TracyLiu_tju@163.com
李新阳(1971-),男,博士,研究员,主要从事自适应光学相关技术方面的研究。E-mail:xyli@ioe.ac.cn
版权所有©2020中国科学院光电技术研究所
