截割机构延迟特性对巷道断面成型精度影响分析
2020-04-23刘治翔谢春雪
刘治翔,谢 苗,谢春雪,毛 君
(辽宁工程技术大学 矿产资源开发利用技术及装备研究院,辽宁 阜新 123000)
随着科学技术的不断进步,煤矿井下掘进机正向更加复杂化、自动化和智能化的掘进机器人方向发展[1]。目前掘进机的截割作业主要依靠人工就地操作完成,人工操控不仅会加重煤矿工人工作强度,而且人工操控实现的截割控制精度低、截割成形误差较大,难以满足煤矿日益增长的生产效率的要求以及实现工作面少人化、无人化的发展需求[2-3]。近些年来许多专家学者针对掘进机自动截割控制技术进行了深入研究。
董磊[4]等利用UG软件对掘进机回转机构建立三维模型,通过仿真分析,得到3种工况仿真曲线,并对仿真结果进行了分析,为优化设计和有限元分析等提供了理论依据。李旭等[5]将微分几何理论应用到巷道空间掘进机工作机构建模中,建立其运动学方程并求解,验证了微分几何法用于研究掘进机运动规律的可靠性。商跃[6]基于悬臂式掘进机回转机构工作原理,构建其三维模型,并对该机构进行了运动学分析及仿真,得到了回转力矩与摆角的参数关系。苏杭等[7]运用了D-H 坐标系方法构建了掘进机截割头和掘进机机体的在空间坐标系的位置关系。田劼等[8-10]构建了掘进机空间位姿坐标系与运动学模型,研究了掘进机截割头空间坐标精确定位以及其轨迹规划控制的数学模型。吴淼等[11]建立了悬臂式掘进机位姿监测模型,并进行了仿真分析,同时提出了一种自主监测方法。杜雨馨等[12]基于掘进机机身和十字激光面的位置关系,构建了该机构的位姿数学模型,解决了掘进机位置和姿态实时监测的问题。毛君[13]等构建了截割机构的数学模型,揭示了掘进机截割机构与截割头外包络位置的空间关系。
由于煤矿井下是高粉尘、高污染以及高电磁干扰的复杂环境,不利于电液比例阀和电液伺服阀工作的可靠性。再加之电液比例阀和电液伺服阀控制技术复杂、成本高,目前电液比例阀和电液伺服阀控制技术还没有在煤矿井下掘进机中得到普及。由于执行元件响应时间差、负载干扰以及液压油液的压缩性等多因素的干扰,使得手动换向阀或电磁换向阀控制掘进机截割煤岩时存在较大延迟,断面成型精度较低。因此考虑截割部执行机构延迟特性对截割误差的影响,提高巷道断面成型精度是本文研究的重点内容。
1 截割系统介绍
项目组研发一种双组纵轴悬臂式截割系统,通过液压控制系统控制垂直摆动油缸、前后推移油缸、回转油缸实现截割头到达工作空间的指定位置,通过截割臂控制截割头截割煤岩。图1为截割升降回路原理图。截割横摆回路与升降回路基本一致。工作系统通过电机驱动变量泵供油,通过操作多路阀,液压油进入平衡溢流阀组和截割升降油缸,完成截割部的升降。将平衡溢流阀组设置于多路换向阀和截割升降油缸之间[14]。
本文在研究截割部执行机构延迟特性对截割误差的影响时暂不考虑机身姿态、位置等变化对截割精度的影响。通过与截割部水平伸缩油缸、升降油缸和水平摆动油缸一起安装的高精度磁致伸缩位移传感器,分别测量截割部水平位移、升降角度和水平摆动角度。再通过截割部正向运动学分析解出截割头在巷道坐标系中的位置。
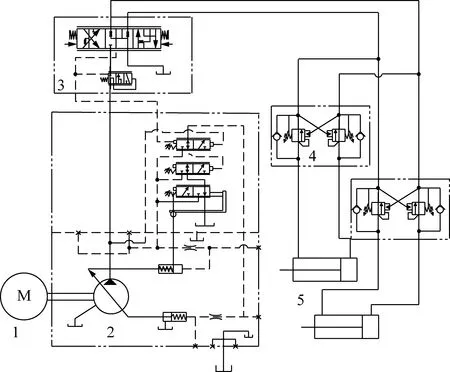
图1 截割机构液压系统原理Fig.1 Hydraulic system principle of cutting mechanism1—电机;2—A11VO260LRDS变量泵;3—M4多路换向阀; 4—平衡溢流阀组;5—截割升降油缸
2 截割机构运动学分析
2.1 截割部运动学基本参数建模与求解
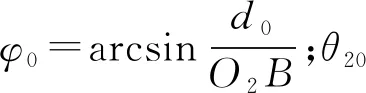
由截割部垂直摆动θ2与截割头中心距地面的高度h的几何关系,可得
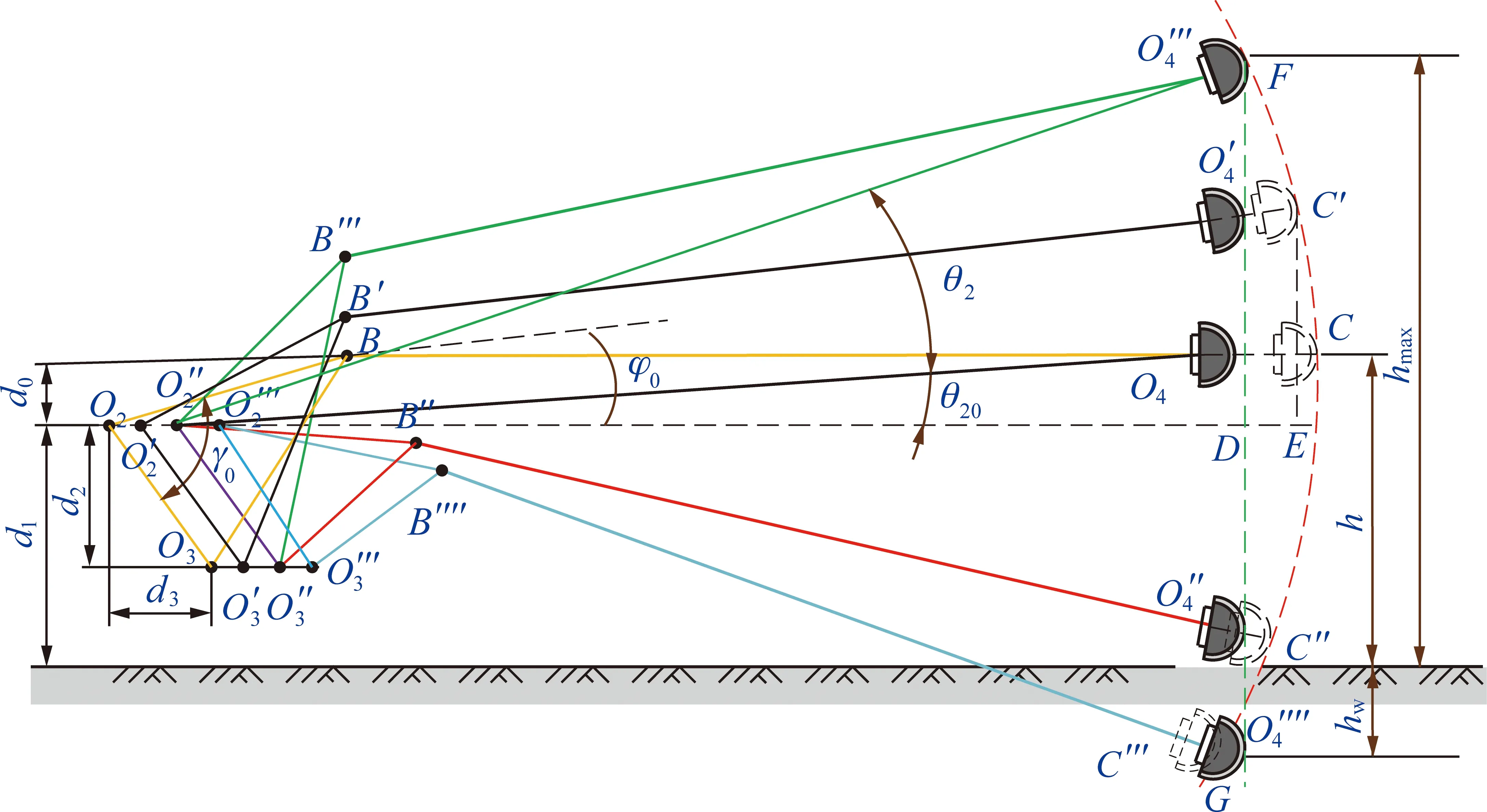
图2 截割部垂直摆动示意Fig.2 Schematic diagram of vertical swing of cutting part
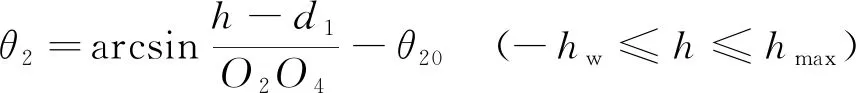
(1)
式中,h为截割头中心和地面的距离;d1为截割部回转中心与地面的高度。
当截割部垂直摆动θ2角时,升降油缸AB的长度l2为

(2)
式中,γ0为O2O3与O2B的夹角。
在截割头处于任意位置时,推移油缸的位移d为
d=O2O4[1-cos(θ2+θ20)]
(3)
截割部水平摆动简图如图3所示,其中,ξ0为液压缸后铰点与前铰点构成的安装位置角;θ1为截割部水平旋转;b为截割头中心距机体中心线的距离;c1为水平推移油缸铰耳与截割部回转中心的距离;c2为水平推移油缸铰耳至机体中心线的距离。

(4)
则两个摆动油缸的长度为
l1c=
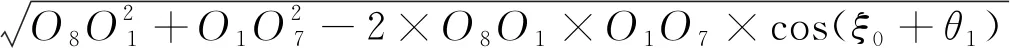
(5)
l1d=
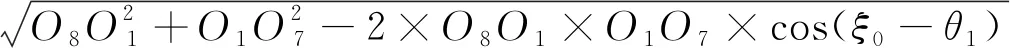
(6)
2.2 截割部坐标变换
根据D-H方法[16-17]建立掘支锚机组截割部各关节的坐标系和连杆参数设定如图4所示,图中,i=1,2,分别表示左侧截割部和右侧截割部;bi1为机身坐标原点到截割部进给油缸铰接点的垂直距离;bi2为截割部进给油缸铰接点到截割部回转中心的垂直距离;ai1+di为机身坐标原点到截割部进给油缸铰接点的水平距离;ai2为截割部回转中心到截割部进给油缸铰接点的水平距离;ai3为截割部升降铰接点到回转中心的水平距离;ai4为截割头中心到截割部升降铰接点的水平距离;bi3为截割头中心到截割部升降铰接点的垂直距离。
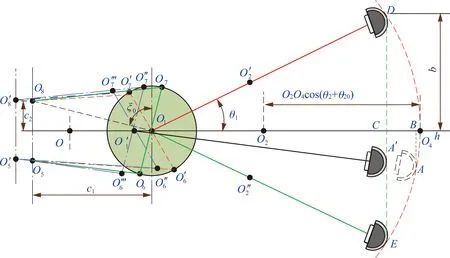
图3 截割部水平摆动示意Fig.3 Schematic diagram of horizontal swing of cutting part

图4 截割部各关节坐标系统及连杆参数Fig.4 Coordinate system of cutting part and connecting rod parameters
根据截割部各关节的坐标系,使用改进D-H方法得到各连杆参数见表1。表1中,i=1,2,分别表示左侧截割部和右侧截割部;aij-1为从Zi-1轴到Zi轴沿Xi轴测量的距离;αij-1为从Zi-1轴到Zi轴绕Xi轴旋转的角度;dij为Xi-1轴到Xi轴沿Zi轴测量的距离;θij为从Xi-1轴到Xi轴绕Zi轴旋转的角度。
由表1所述的各个连杆的参数,可得各个连杆之间的变换为
表1 各个连杆的参数
Table 1 Link parameters

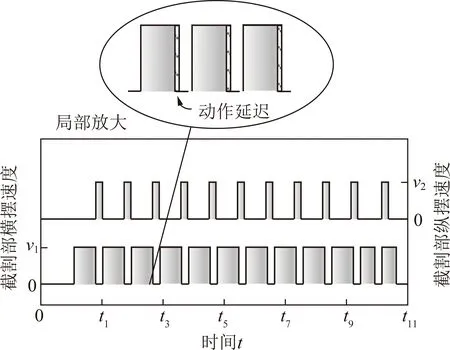
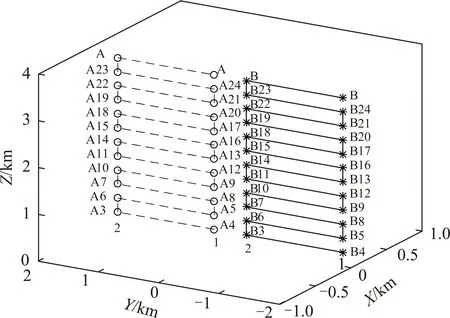
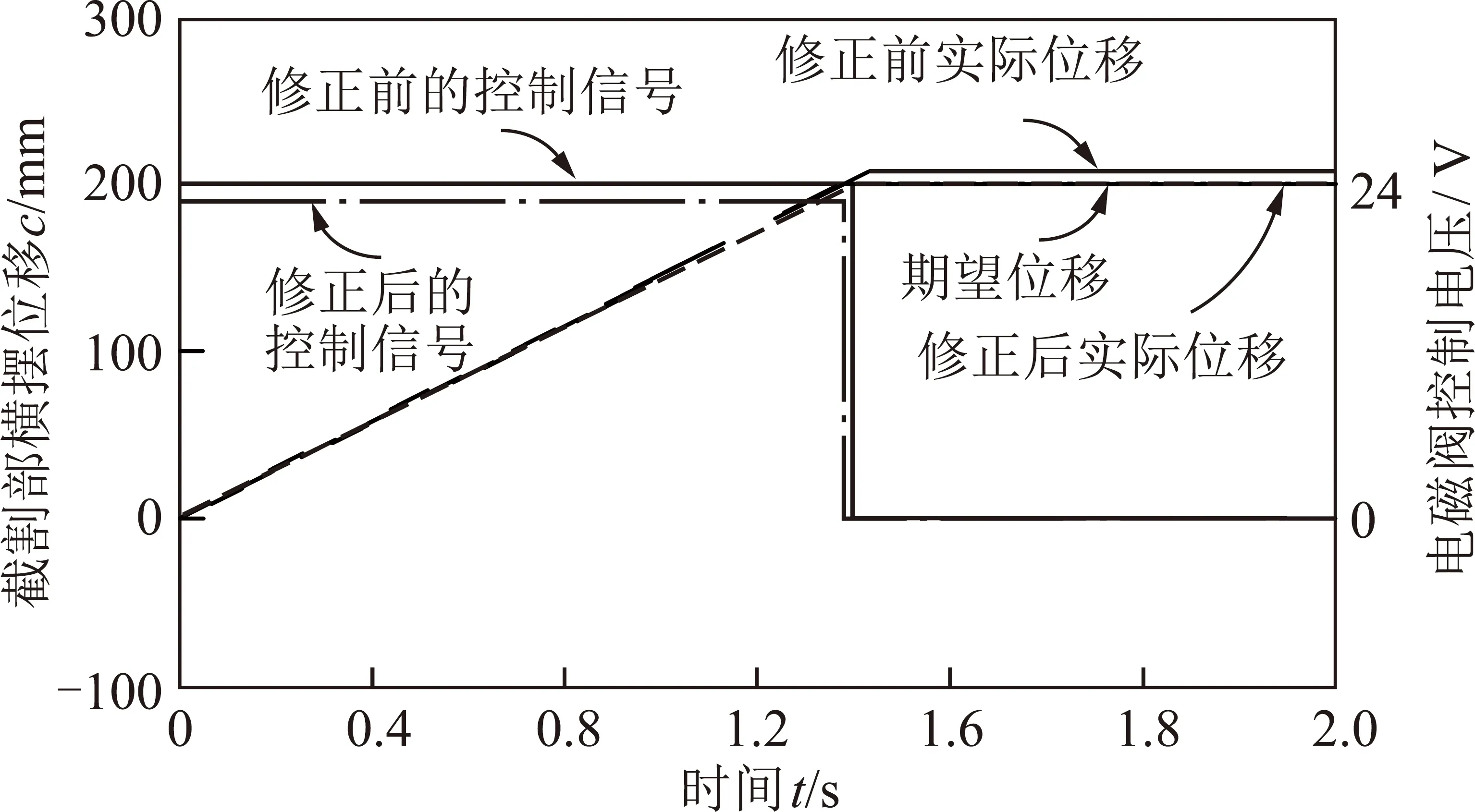
连杆ijaij-1αij-1/(°)dijθij/(°)变量变量范围i1ai1+di0bi10di0 (7) 可得在掘支锚机组坐标系OVXVYVZV中对截割头进行描述的齐次变换矩阵[18]为 (8) 设在截割头坐标系中截割头中心的坐标向量为i4p=[0 0 0 1]T,则通过下式可将其转换到掘支锚机组的坐标系中: (9) 由式(9)可知随着截割部的运动,截割头的坐标如下: (10) 在进行巷道断面的定形定向截割时,需要通过截割部运动规划将截割头运动轨迹规划到驱动截割头运动的水平回转油缸、垂直升降油缸以及推移油缸的输出行程上。截割部运动主要是水平摆动和垂直摆动,将巷道轮廓内部煤岩截割掉,形成所需要的断面形状。将其转换为以驱动油缸位移量为变量的表达式: (11) 式中, γ0为AO2B的角度。 实际上,从中央控制器发送执行指令到各个油缸接收到动作指令,再到各个油缸执行完指令,这一过程是存在延迟的。各个油缸的动作不能够按照理想情况下的动作时序进行,截割断面时存在动作延迟情况下各个油缸的动作时序如图5所示。 图5 存在动作延迟情况下各个油缸的动作时序Fig.5 Time series diagram of each cylinder with action delay 设截割部横摆动作延迟时间为td1,纵摆动作延迟时间为td2,则截割头的坐标表达式为 (12) 因此,可得在横摆截割时由于动作延时带来的截割头中心在巷道断面坐标系y轴上的运动误差为 Ey=ai3(S′i1-Si1)+bi3(C′i2S′i1-Ci2Si1)- ai4(S′i1S′i2-Si1Si2) (13) 在纵摆截割时由于动作延时带来的截割头中心在巷道断面坐标系z轴上的运动误差为 Ez=ai3(Ci2-C′i2)+bi3(Si2-S′i2) (14) 截割头中心在巷道断面坐标系x轴上的运动误差不会影响巷道断面成型精度,故在此不研究动作延时带来的截割头中心在巷道断面坐标系x轴上的运动误差。 使用MATLAB软件对本文研究内容进行仿真研究。设定巷道断面尺寸为巷道顶部圆弧的半径Rs=2 m;圆弧半角α为120°。截割部的运动学模型中的主要参数如下:a1=1 400 mm;a2=500 mm;a3=650 mm;a4=5 000 mm;b1=200 mm;b2=1 000 mm;b3=150 mm;d=0 mm;-30°≤θ11≤15°;-130°≤θ12≤-60°;-15°≤θ21≤30°;-130°≤θ22≤-60°。设定巷道断面坐标系的YOZ平面与掘支锚机组的YOZ平面平行。 理想情况下各个油缸的动作不存在延迟,得到的截割轨迹如图6所示。 图6 理想情况下的截割轨迹Fig.6 Cutting trajectory under ideal conditions 巷道断面截割轨迹中,左截割头按照A1→A2→A3→A4→…→A22→A23→A24的顺序进行巷道截割;右截割头按照B1→B2→B3→B4→…→B22→B23→B24的顺序进行巷道截割。 为研究不同截割延迟对截割精度的影响,令控制延迟td=50,100和200 ms,截割横摆速度恒定,得到截割轨迹如图7所示。 图7 存在延迟情况下的截割轨迹Fig.7 Cutting trajectory with delay 在横摆速度恒定的情况下,当延迟时间分别为td=50,100和200 ms时,横摆截割的截割轨迹误差分别为10,20以及40 mm。 为研究不同截割横摆速度对截割精度的影响,分别令截割横摆速度为200,100和50 mm/s,得到截割轨迹如图8所示。 图8 不同横摆速度情况下的截割轨迹Fig.8 Cutting trajectory at different yaw speeds 当横摆速度分别为v2=50,100和200 mm/s时,横摆截割的截割轨迹误差分别为5,10以及20 mm。可见随着截割部横摆速度和动作延迟的增大,截割轨迹误差随之增大。由于普通的开关电磁换向阀不易于进行流量实时调控,因此无法做到对截割部横摆速度的缓冲控制。需要充分掌握截割执行机构的延迟特性,在控制系统中做好提前量,消除动作延迟带来的截割误差。 本课题组以实验室的条件为基础,在此条件下研制出了掘支锚机组实验平台[17],该实验平台由以下3个部分组成:① 掘支锚机组实验模型样机;② 巷道模拟实验台;③ 测试平台,掘支锚机组实验平台如图9所示。 图9 模拟实验平台Fig.9 Simulation experiment platform 本文研究的掘支锚机组采用两个截割部,提高截割部的截割效率和巷道成形轮廓的平整性。通过对各个执行油缸伸缩位移的监测,测试本实验台中掘支锚机组的截割部动作延迟。实测结果可知,本实验台截割部执行机构存在53 ms的延迟,通过对控制系统进行提前量控制,即截割部位移传感器在到达指定位移之前的200 mm/s×53 ms 位置下达停止指令,得到的修正前后的截割动作延迟实验结果,如图10所示。 图10 截割动作延迟实验结果Fig.10 Experimental results of cutting action delay 修正后的截割动作延迟实验结果可知,在掌握了截割执行机构的延迟特性后,在控制系统中做好提前量,即可消除动作延迟带来的截割误差。开关电磁阀的响应时间、油液压缩性、液压系统特性以及负载特性等均会为截割动作带来延迟。目前受实验条件限制仅对特定实验室工况下的截割延迟特性进行研究,后续需要对上述因素影响下的截割延迟时间进行精确地定量分析,多影响因素与延迟特性的函数关系或者离散数据库,以便控制系统根据截割工况和系统自身特性及时修正控制参数,实现精确控制。 (1)根据掘支锚机组截割部系统硬件组成建立了掘支锚机组截割部运动学模型,建立了存在动作延迟下截割控制误差方程。 (2)进行截割控制误差的仿真和实验研究,本文仿真工况下,在横摆速度恒定的情况下,当延迟时间分别为td=50,100和200 ms时,横摆截割的截割轨迹误差分别为10,20以及40 mm。当横摆速度分别为v2=50,100和200 mm/s时,横摆截割的截割轨迹误差分别为5,10以及20 mm。随着截割部横摆速度和动作延迟的增大,截割轨迹误差随之增大。需要充分掌握截割执行机构的延迟特性,在控制系统中做好提前量,消除动作延迟带来的截割误差。 对于不同工况和不同系统软硬件参数影响下,截割过程的动作延迟特性规律将在后续进行研究。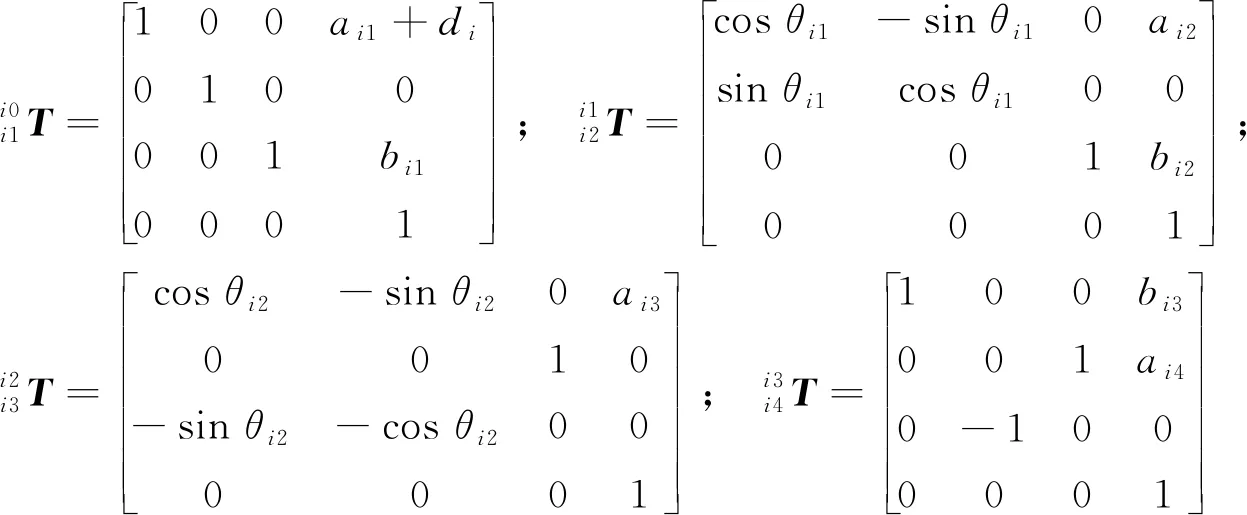

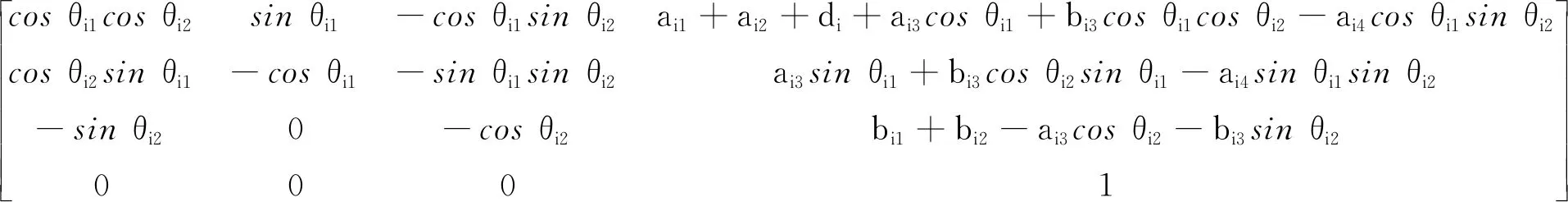
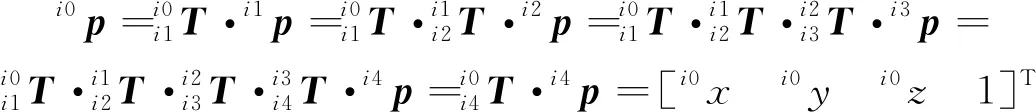
3 动作延迟对截割控制影响分析
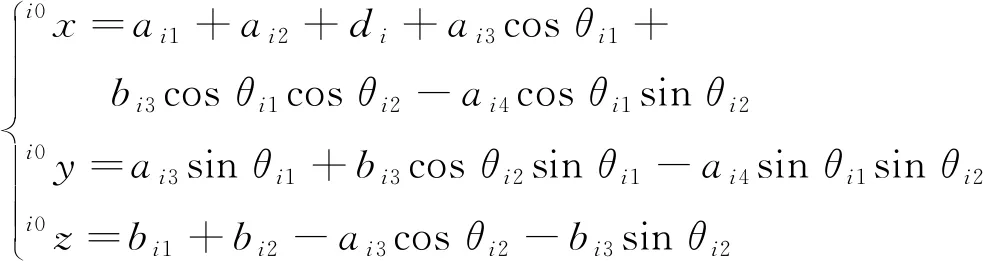
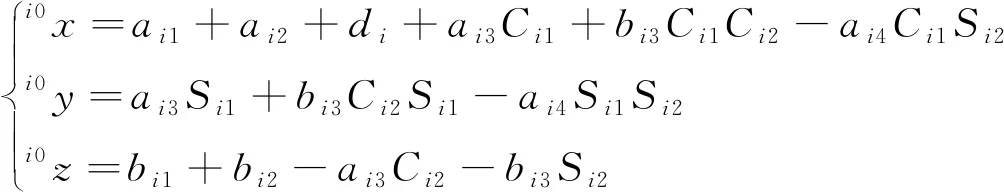

4 截割误差仿真分析


5 实 验

6 结 论
