冷轧钢卷内部应力的影响因素研究

2020-04-23供稿张春杰宋征ZHANGChunjieSONGZheng

金属世界 2020年2期

供稿|张春杰，宋征 / ZHANG Chun-jie, SONG Zheng

内容导读

冷轧带钢卷的内部应力场的分布规律是影响卷取过程板形缺陷的主要因素之一。为了研究冷轧带钢卷的内部应力，本文把带钢卷径向弹性模量作变量处理，考虑了带钢卷的各向异性，以每层带钢的厚度中心为基准，根据弹性力学轴对称理论，列出带钢的层间径向位移和应力的方程式，从而计算出带钢卷内部应力。同时研究了带钢厚度、卷取初始张力对带钢卷内部应力分布的影响，并采用定性实验对计算结果进行进一步验证。

冷轧带钢的卷取过程中，带钢卷内应力场不断变化，会产生错层、折边和层间粘结等缺陷。此外，在卸载过程中，带钢卷的内应力发生变化导致重新分布，会出现一定的平整度缺陷，如下凹(塌卷)、内凸(心型卷)等[1-4]。为了解决这些缺陷问题，国内外学者对冷轧带钢卷的内应力进行了大量的理论分析与探讨[5-10]。周国盈[6]把钢卷作为连续带环多层组合的弹性圆筒，并考虑了钢卷层间的摩擦，运用每卷一层钢卷对卷筒施加一次径向压力增量，累加这些应力增量得出考虑缩径的卷筒的径向压力。计算时把卷取张力(周向应力)取平均值，然而周向应力是逐层变化的，把径向弹性模量当常量处理，没有考虑钢卷的各向异性。Wang等[7]在计算冷轧带钢卷取过程中的应力时忽略了带钢层间径向弹性模量的变化。连家创[8-10]开始用逐层迭代的方法导出钢卷的径向压力方程，但是在迭代的过程中，各参数、迭代次数与迭代精度如果选择不当，迭代可能就会失败，且连家创的这些公式只适用于不考虑卷筒缩径的钢卷内部应力的求解。本文考虑了带钢卷的各向异性，推导带钢卷取过程中逐层内应力的求解方程，分析了冷轧带钢卷取过程中的内部应力分布并对计算结果做了定性实验进行验证。

钢卷内部应力场求解力学模型

假设钢卷处于轴对称应力状态，逐层卷取过程中，卷取第i层后第j层带钢的内圈的径向压力等于卷取第i-1层后第j层带钢的内圈的径向压力与卷取第i层后第j圈带钢内圈的径向压力增量之和，卷取第i层后第j层带钢的内圈的周向应力等于卷取第i-1层后第j层带钢的内圈的周向应力与卷取第i层后第j圈带钢内圈的周向应力增量之和。

钢卷内层径向压力

将卷筒当作厚壁圆筒，内表面不受压力，外表面受压p1时，钢卷内表面径向位移u1等于卷筒外表面径向位移u0。

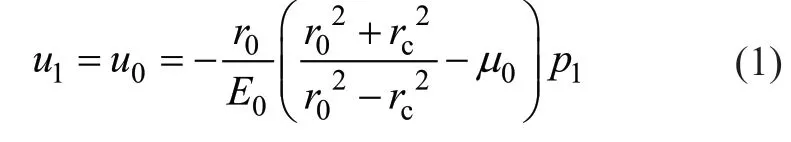
式中：r0、rc分别为卷筒的外半径和内半径；E0、μ0分别为卷筒材料的弹性模量和泊松比。

如图1所示，在钢卷中去除单元体，将单元体所受的各力投影到单元体中心的径向轴上，令并略去高阶无穷小，则得平衡方程式

式中：σj为卷上n圈带钢后第j层带钢的实际张力；pj、pj+1分别为卷上n圈带钢后第j层带钢的内圈径向压力和外圈径向压力。

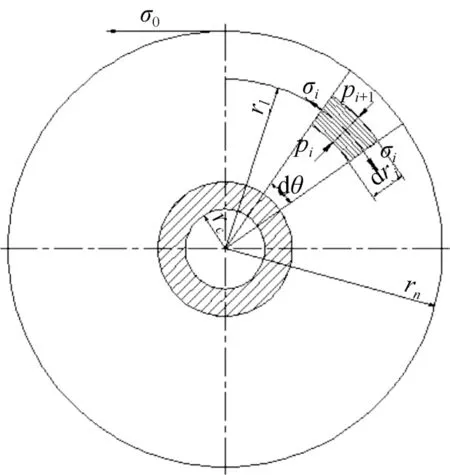
图1 钢卷径向压力计算简图

卷取时，令带钢的单位张力为σ0，则得

式中：T为卷取时带钢的总张力；b、h分别为带钢宽度和厚度。

将板带卷取过程简化为逐层卷取过程，计算钢卷内部应力状态时，可以看成是轴对称问题，即钢卷的形变和应力与极角θ无关。

式中：rj,j为卷取第j层时第j层带钢的半径；u、r分别为任意层带钢的径向位移和半径；uj、uj+1分别为卷上n圈带钢后第j层和j+1层带钢的径向位移。

对于广义平面应力状态，切向应变方程如下：

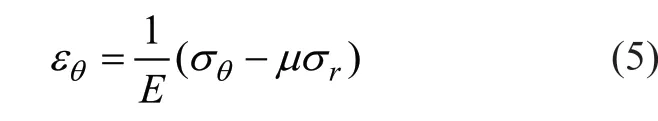
式中：E、μ分别为带钢的弹性模量和泊松比。

卷上去的带钢原来张力为σ0，由于外圈压力使内圈产生变形εθ，从而引起周向应力的变化。

钢卷的径向变形除了一般的弹性形变外，还应考虑每层带钢相互接触时所引起的附加变形。

式中：σr为任意层带钢的径向应力；εn为带钢接触表面相互压紧时所引起的附加变形；En为带钢接触表面的紧密系数。

其中，

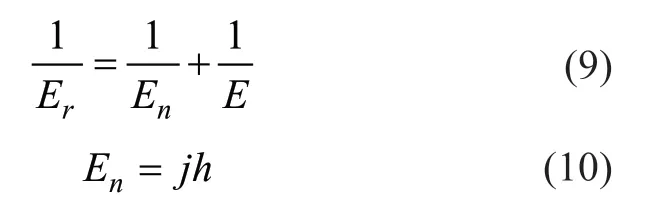
式中：Er为钢卷径向压缩系数，它与带钢厚度、表面粗糙度等因素有关；j为接触表面的刚度系数， kg/cm³。

参考文献[10]，根据古谢夫的推导，再把式(10)代入式(9)得

对于最后一圈即第n层，外表面压力等于零，即pn+1=0，带钢的实际张力为σn=σ0，利用平衡方程式(2)得

考虑卷取第i层时对第j层带钢的影响时的内应力

带钢在卷取过程中，每加卷一层都会使其内其余层带钢压力有所释放，钢卷内的应力将重新分布。最终钢卷内的径向和周向应力的大小和分布，决定了钢卷在后续运输和存放过程的稳定性。因此，为了精确计算钢卷平面问题，必须考虑带钢卷取第i层时，钢卷内第j层带钢径向和周向应力的变化规律以及钢卷内第j层带钢径向应力与钢卷稳定性的关系，进而建立一套相对准确的卷取张力体系。考虑卷取第i层时对第j层带钢应力影响，根据图1计算时，σr用径向压力表示，综上得：

式中：ui,j、ui,j+1分别为卷取第i层时第j层带钢内圈径向位移和外圈径向位移；pi,j、pi,j+1分别为卷取第i层时第j层带钢的内圈径向压力和外圈径向压力；ri,j、hi,j分别为卷取第i层时第j层带钢半径和厚度。

冷轧带钢内部应力影响因素的分析

在本文理论计算中，冷轧带钢的基本卷取参数选取以燕山大学轧制中心实验室二十辊轧机为例进行分析。冷轧卷取模拟理论计算参数，设定卷取圈数为300圈，实心卷筒的外半径r0=52 mm，卷筒的内半径rc=32.5 mm，卷筒的弹性模量和泊松比分别为E0=2.1×105MPa，μ0=0.28，带钢的弹性模量和泊松比分别为E=2.1×105MPa，μ=0.28，表面粗糙度Ra=0.0008 mm，微观粗糙度Δ=0.0032 mm，板形系数η=0.01，修正系数k0=0.45。

不同带钢厚度的影响

设定卷取初始张力35 MPa，针对厚度分别为0.2和0.4 mm的带钢卷取过程进行了分析。

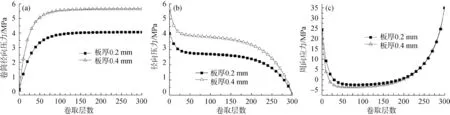
图2 不同带钢厚度对冷轧带钢内部应力分布的影响： (a) 卷筒所受径向压力的变化；(b) 钢卷逐层径向压力分布；(c) 钢卷逐层周向应力分布

图2 (a)表明，在冷轧带钢卷取初期卷筒的径向压力迅速增加，卷取中后期卷筒的径向压力将达到稳定值，继续卷取，外层钢卷对卷筒的径向压力几乎没有影响；在冷轧带钢卷取过程中卷筒所受径向压力都随着带钢厚度的增加而逐渐增大。图2(b)显示，无论是钢卷内层、中层还是外层，带钢逐层径向压力都随着带钢厚度的增加而逐渐增大。图2(c)显示，在冷轧带钢卷取完成后，带钢逐层周向应力都随着带钢厚度的增加而略微降低。

不同初始张力的影响

针对带钢厚度为0.2 mm，设定卷取初始张力分别为35、50和65 MPa的带钢卷取过程进行了分析。

图3(a)表明，在冷轧带钢卷取过程中卷筒所受径向压力都随着初始张力的增加而逐渐增大。图3(b)表明，在冷轧带钢卷取完成后，无论是钢卷内层、中层还是外层，钢卷逐层径向压力都随着初始张力的增加而增大。图3(c)表明，带钢逐层周向应力在钢卷内层和钢卷外层都随着卷取初始张力的增加而减小，而在钢卷中层随着初始卷取张力的增加而增大。

定性实验

定性实验的基本卷取参数选取以燕山大学轧制中心实验室二十辊轧机为例进行分析。其他参数与理论计算参数相同，实验室温度T=15℃，湿度RH=20 g/m³。

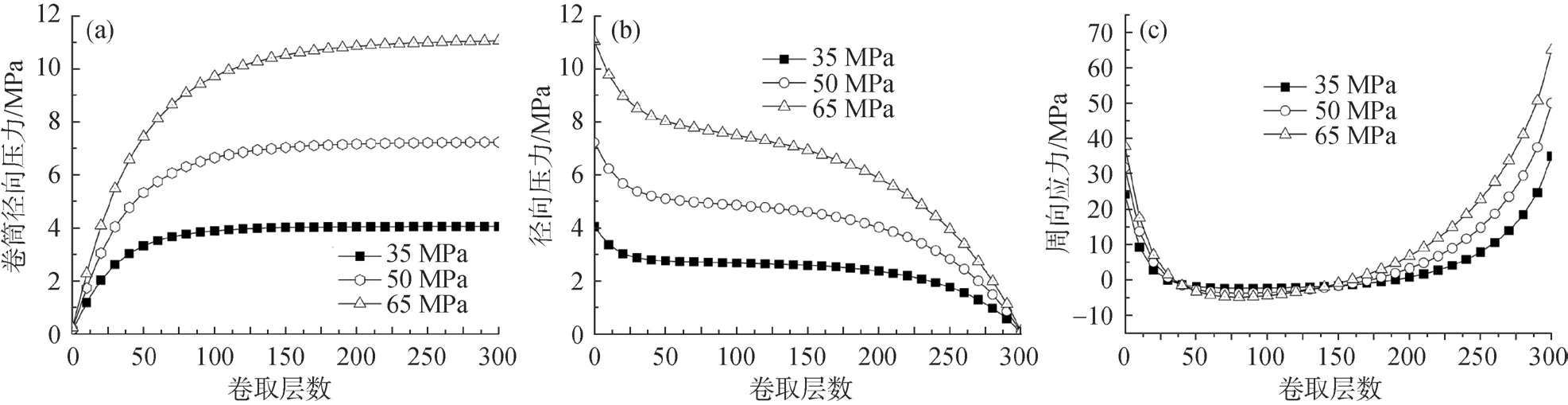
图3 不同初始张力对冷轧带钢内部应力分布的影响： (a)卷筒所受径向压力的变化；(b)钢卷逐层径向压力分布；(c)钢卷逐层周向应力分布

(1) 取带钢厚度0.2 mm，卷取初始张力35、50、65 MPa时，测量卷筒所受的径向压力，设置好二十辊轧机的相应参数，将已经准备好大小适中的感压纸放在卷取中的第1层带钢中，在卷完第50层后停留2 min然后卸卷，取出感压纸。如图4所示，对比标准比色卡，实验测感压纸(a)的读值是3～4 MPa，(b)的读值是5～6 MPa，(c)的读值是7～8 MPa。实验测得值与理论计算值比较接近，在带钢卷取厚度相同卷取层数相同时，卷筒所受的径向压力都随着卷取初始张力增加而逐渐增大。

图4 不同初始张力感压纸实测结果： (a) 35 MPa；(b) 50 MPa；(c) 65 MPa

(2) 取带钢厚度0.2 mm，卷取初始张力35 MPa时，测量不同层数带钢的径向压力，设置好二十辊轧机的相应参数，将已经准备好大小适中的感压纸放在卷取中的第1层带钢中，首先逐层卷取50层完成后停留2 min然后卸卷，取出感压纸。重复上述实验步骤卷取层数分别为卷取100层、150层、200层完成后停留2 min然后卸卷，取出感压纸。如图5所示，对比标准比色卡，实验测感压纸(a)的读值是3～4 MPa，(b)的读值是4 MPa左右，(c)的读值是4 MPa左右。实验测得值与理论计算值比较接近，在带钢卷取厚度相同卷取初始张力相同时，卷筒所受的径向压力未达到稳定之前是随着卷取层数增加逐渐增大，而达到稳定之后不再发生变化。

图5 不同卷取层数感压纸实测结果： (a) 50；(b) 100；(c) 150；(d) 200

(3) 取带钢厚度分别为0.2和0.4 mm，卷取初始张力35 MPa时，测量卷取300层后第50层带钢所受的径向压力，设置好二十辊轧机的相应参数，将已经准备好大小适中的感压纸放在卷取中的第50层中，继续卷取直到300层后停留2 min然后卸卷，取出感压纸。如图6所示，对比标准比色卡，实验测感压纸(a)的读值是3～4 MPa，(b)的读值是5～6 MPa。实验测得值与理论计算值比较接近，在卷取初始张力相同卷取层数相同时，钢卷所受的径向压力随着带钢厚度的增加而增大。